
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
долгосрочной финансовой политики
Цели деятельности предприятия отличаются, но имеют тенденцию принадлежать к двум типам.
Первый относится к прибыльности. Эта цель включает в себя объем продаж, сектор рынка и контроль над расходами, что относится, по крайней мере, потенциально, к различным способам получения или увеличения прибыли.
Как правило, эта цель получает конкретное выражение в обеспечении максимизации рыночной стоимости предприятия. Повышение достатка владельцев фирмы заключается не столько в росте текущих прибылей, сколько в повышении рыночной цены их собственности.
Второй тип, включающий избежание банкротства, стабильность и безопасность, относится некоторым образом к контролированию риска.
Иногда в стратегические цели предприятия включены и внеэкономические составляющие, такие как мотивация власти, престижа, безопасности собственников, руководства. Кроме того, не нужно пренебрегать и тем фактом, что крупные компании подвергаются давлению со стороны государства, и вынуждены брать на себя общественные, экологические и иные цели, часто идущие вразрез с их внутренними целями и, особенно, с целями самих собственников.
Эти два типа целей в некоторой степени противоречат друг другу. Погоня за прибылью обычно сопряжена с повышенным риском, а отказ от использования заемного капитала, хранение существенных остатков денежных средств и др. меры по обеспечению финансовой устойчивости снижают рентабельность производства. Таким образом, невозможно максимизировать одновременно и безопасность, и прибыль.
Для того чтобы финансовая политика приобрела системный характер стратегические цели необходимо ранжировать путем задания весов и введения составного критерия. Каждый из частных критериев отражает разные и нередко противоречивые показатели, имеющие свою размерность. Составной критерий при этом может не иметь ясно выраженного экономического смысла. Его можно рассматривать лишь как меру предпочтительности. Веса каждого из показателей устанавливаются, как правило, экспертным путём.
Более методически правильным способом выбора лучшего варианта финансовой политики предприятия является выделение одного их критериев в качестве главного и использование других в качестве ограничений.
Так, если главной целью считать достижение максимальной рыночной стоимости предприятия (W1), а показатели риска (W2), соблюдения экологических требований (W3), престижа (W4) и т.д. отнести к ограничениям, то лучшим будет такой вариант финансовой политики, который позволит обеспечить максимальную рыночную стоимость предприятия (max W1) при:
– показателях риска не выше заданных (W2 ≤ Wзад.);
– соблюдении экологических требований (W3 ≥ Wтреб.);
– достижении требуемых показателей престижа (W4 ≥ Wтреб.).
Иначе говоря, найти такой вариант финансовой политики, при котором W1 стремится к максимуму, а W2 ≤ Wзад., W3 ≥ Wтреб., W4 ≥ Wтреб..
Если же главным показателем будем считать уровень риска (W2), то лучшим будет вариант при котором риск сводится к минимуму (W2 → min), а W1 ≥ Wтреб., W3 ≥ Wтреб., W4 ≥ Wтреб..
При такой постановке задачи имеют ясный смысл и позволяют найти оптимальное решение из числа допустимых по условиям-ограничениям.
Задачи решаются в такой последовательности. После формирования различных вариантов финансовой политики производится оценка каждого из них выделенными показателями. Затем задача формулируется в общем виде как задача максимизации или минимизации главного показателя. Для выбранной постановки задачи исключаются варианты не удовлетворяющие ограничениям, т.е. оставляются только допустимые варианты из которых выбирается лучший в смысле выбранного критерия. Так, если главным критерием назван показатель рыночной стоимости предприятия W1, то из числа допустимых по ограничениям вариантов выбирается тот, который имеет максимальное значение W1.
Например, возможны три варианта инвестирования денежных средств. Каждый из вариантов характеризуется набором показателей:
W1 - рост рыночной стоимости организации, %;
W2 - риск успешной реализации проекта, баллы;
W3 - степень соблюдения экологических требований, %.
Очевидно, что показатель W1 находится в противоречии с показателями W2 и W3 . Стремление повысить рыночную стоимость организации неминуемо увеличивает риск и снижает возможности соблюдения экологических требований.
Результаты оценки показателей по всем вариантам представлены в таб.3.1.
Таблица 3.1
Варианты инвестирования средств
| Показатель | Вариант | ||
| I | II | III | |
| W1 Рост рыночной стоимости, % | |||
| W2 Риск успешной реализации проекта, баллы | |||
| W3 Степень соблюдения экологических требований |
Выбор варианта, обеспечивающего максимальный рост рыночной стоимости организации осуществим в два этапа.
Первый этап – проверка соблюдения ограничений. Если риск не может превышать 50 баллов (W2 ≤ 50), а соблюдение экологических требований должно быть не менее 80% (W3 ≥ 80), то первый вариант следует исключить (W2 = 60 > 50).
Второй этап – выбор лучшего варианта по заданному критерию. Из оставшихся второго и третьего вариантов второй обеспечивает максимальный рост рыночной стоимости (20 > 10), поэтому он является лучшим.
Но в качестве критерия может быть выбран и показатель риска успешной реализации проекта. В этом случае лучшим следует считать вариант, обеспечивающий минимальный риск. Используем методику выбора варианта, аналогичную предыдущей задаче.
Первый этап – проверка соблюдения ограничений. Если рост рыночной стоимости должен составить не менее 10% (W1 ≥ 10), а соблюдение экологических требований должно быть не менее 80% (W3 ≥ 80), то все три варианта удовлетворяют ограничениям.
Второй этап – выбор лучшего варианта по заданному критерию. Из рассматриваемых вариантов третий обеспечивает минимальный риск (10 < 30 и 20), поэтому он является лучшим.
Разработанная финансовая политика не может быть раз и навсегда определенной и незыблемой. Последние годы показали, насколько фундаментальными могут быть изменения в условиях хозяйствования. Кроме того, стремительные изменения продолжаются и в настоящее время на финансовых рынках, со стороны регулирования государством, в практике управления предприятием. Поэтому финансовая политика должна быть гибкой и учитывать изменения всех интересов и факторов, оказывающих на нее влияние.
В этой связи одним из основных принципов финансовой политики является то, что она должна строиться не столько из фактически сложившейся ситуации, сколько из прогноза ее изменения. Только на основе предвидения финансовая политика приобретает устойчивость.
1.3. Методы формирования долгосрочной финансовой политики предприятия
Эквивалентность процентных ставок различного типа
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые результаты.
Обозначения, использованные ранее:
i – простая годовая ставка ссудного процента;
d – простая годовая учетная ставка;
ic – сложная годовая ставка ссудного процента;
dc – сложная годовая учетная ставка;
Приравнивая попарно формулы для определения наращенной суммы, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.
Приравнивая соотношения 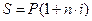 и
и  , получим:
, получим:
– простая годовая ставка ссудного процента 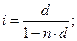 (3.1)
(3.1)
– простая годовая учётная ставка  (3.2)
(3.2)
Пример 1
Срок уплаты по долговому обязательству – полгода, учетная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?
Решение
Используем формулу простой годовой ставки ссудного процента (3.1)

Ответ: простая ставка ссудного процента равна 19,8%.
Пример 2
Кредит выдан на полгода по простой ставке ссудного процента 19,8% годовых. Какова доходность данной операции, приемлемой в виде простой учётной ставки?
Решение
Используем формулу простой учётной ставки 3.2

Ответ: простая учётная ставка равна 18%.
Из формул 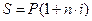 и
и  можем получить эквивалентные ставки простой и сложной годовой ставки ссудного процента:
можем получить эквивалентные ставки простой и сложной годовой ставки ссудного процента:
– простая годовая ставка ссудного процента  (3.3)
(3.3)
– сложная годовая ставка ссудного процента  (3.4)
(3.4)
Пример 3
Первоначальная сумма 300 000 руб. вложена на 2 года с использованием сложной годовой ставки ссудных процентов в размере 16%. Определить эквивалентную простую годовую ставку ссудных процентов.
Решение
Используем формулу 3.3

Ответ: эквивалентная простая ставка ссудного процента равна 17,28%.
Пример 4
Сумма 300 000 руб. вложена на 2 года с использованием простой годовой ставки ссудных процентов в размере 17,28%. Определить эквивалентную сложную ставку ссудных процентов.
Решение
Используем формулу 3.4
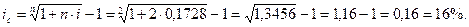
Ответ: эквивалентная сложная ставка ссудного процента равна 16%.
Результаты расчётов в примерах 3 и 4 подтверждают правильность использования формул.
Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы: 
- сложная годовая ставка ссудного процента 
- номинальная ставка ссудного процента 
Полученная сложная годовая ставка ссудного процента (ic) эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов.
Пример 4а
Рассчитать эффективную ставку сложных процентов, если номинальная ставка равна 24% и начисление процентов происходит ежемесячно.
Решение
Вычисление проводим по формуле 

Ответ: эффективная ставка сложных процентов равна 26,8%.
Учет инфляционного обесценения денег в принятии финансовых решений
Пусть Sa — сумма, покупательная способность которой с учетом инфляции равна покупательной способности суммы при отсутствии инфляции. Через ΔS обозначим разницу между этими суммами.
Отношение ΔS /S, выраженное в процентах, называется уровнем инфляции.
При расчетах используют относительную величину уровня инфляции — темп инфляции  .
.

Тогда для определения Sa получаем следующее выражение:
Sα = S+ ΔS= S+ S  = S(1+
= S(1+  ). (3.5)
). (3.5)
Величину (1 +  ), показывающую, во сколько раз Sa больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляции Iи.
), показывающую, во сколько раз Sa больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляции Iи.
Iи = 1 +  .
.
Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение — на уменьшение ее темпов.
Пусть  – годовой уровень инфляции. Это значит, что через год сумма
– годовой уровень инфляции. Это значит, что через год сумма  будет больше суммы
будет больше суммы  в (1 +
в (1 +  ) раз. По прошествии еще одного года сумма
) раз. По прошествии еще одного года сумма 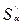 будет больше суммы S'a в (1 +
будет больше суммы S'a в (1 +  ) раз, т. е. больше суммы S в (1+
) раз, т. е. больше суммы S в (1+  )2 раз. Через п лет сумма
)2 раз. Через п лет сумма  вырастет по отношению к сумме S в (1 +
вырастет по отношению к сумме S в (1 +  )n раз. Отсюда видно, что инфляционный рост суммы S при годовом уровне инфляции
)n раз. Отсюда видно, что инфляционный рост суммы S при годовом уровне инфляции  – то же самое, что наращение суммы S по сложной годовой ставке процентов
– то же самое, что наращение суммы S по сложной годовой ставке процентов  .
.
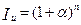 . (3.6)
. (3.6)
Разумеется, те же рассуждения применяются, если вместо года берется любой другой временной интервал (квартал, месяц, день и т. д.).
Очень важно запомнить данную аналогию со сложным процентом, так как одна из наиболее часто встречающихся ошибок, связанных с расчетом уровня инфляции за некоторый период, связана именно с неучётом данного обстоятельства.
Если цены каждый месяц растут на 2%, то за годовой уровень инфляции, недолго думая, принимают 2% • 12 = 24%. Такие расчеты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 25% годовых. Между тем, если уровень инфляции составляет 2% в месяц, это значит, что за месяц цены вырастают в (1 + 0,02) = 1,02 раза, а за год— в 1,0212 = 1,268 раза. Значит, годовой темп инфляции составляет 1,268 - 1 = 0,268, т. е. годовой уровень инфляции достигает 26,8%. После такого расчёта процентная ставка 25% годовых теряет свою инвестиционную привлекательность и может рассматриваться лишь в плане минимизации потерь от инфляции.
Пример 5
Цены каждый квартал растут на 3%. Банк привлекает клиентов вкладывать средства по 13% годовых. Требуется определить, покроет ли такая доходность вклада потери от инфляции.
Решение
1. Определим индекс инфляции по формуле 3.6

2. Определим темп инфляции используя формулу
Iu= 1+ α откуда α = Iu– 1 = 1,1225 – 1 =0,1225 = 12,25%.
Ответ: доход от вклада покроет потери от инфляции.
Если в обычном случае первоначальная сумма Р при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму  , что требует уже иной процентной ставки.
, что требует уже иной процентной ставки.
Назовем ее ставкой процентов, учитывающей инфляцию.
Пусть
 – ставка ссудного процента, учитывающая инфляцию;
– ставка ссудного процента, учитывающая инфляцию;
d  – учетная ставка, учитывающая инфляцию.
– учетная ставка, учитывающая инфляцию.
Зададим годовой уровень инфляции  и простую годовую ставку ссудного процента i. Тогда для наращенной суммы S, превращающейся в условиях инфляции в сумму S
и простую годовую ставку ссудного процента i. Тогда для наращенной суммы S, превращающейся в условиях инфляции в сумму S  получим формулу:
получим формулу:
 (3.7)
(3.7)
Для данной суммы можно записать еще одно соотношение:
 (3.8)
(3.8)
Рассмотрим теперь различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период.
Для простых процентных ставок 
В то же время должно выполняться равенство: 
Составим уравнение эквивалентности:
 из которого получаем
из которого получаем
 (3.9)
(3.9)
Пример 6
При выдаче кредита в сумме 40 млн.руб. должна быть обеспечена реальная доходность операции, определяемая простой процентной ставкой 14% годовых. Кредит выдаётся на полгода, за которую индекс инфляции составит 1,06. Рассчитать значение процентной ставки, компенсирующей потери от инфляции, и наращенную сумму.
Решение
По условию задачи Р=40 млн.руб., n = 0,5 года, I =0,14, Iu= 1,06.
1. По формуле 3.9 определим процентную ставку, компенсирующую потери от инфляции 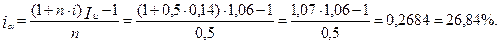
2. По формуле 3.7 определим наращенную сумму
 млн.руб.
млн.руб.
3. Наращенную сумму можно определить и по формуле 3.8
 млн.руб.
млн.руб.
Результаты определения наращенной суммы совпадают.
Для случая сложных процентов для составления уравнения эквивалентности используем формулы:  и
и 
Отсюда  (3.10)
(3.10)
Пример 7
Первоначальный капитал в размере 20 000 руб. выдается на три года, проценты начисляются в конце каждого года по ставке 8% годовых. Определить наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.
Решение
По условию задачи Р = 20 000 руб.; n = 3 года; ic= 0,08; α = 0,12.
1. Для определения индекса инфляции воспользуемся формулой 3.7
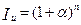 = (1 + 0,12)3=1,4049.
= (1 + 0,12)3=1,4049.
2. По формуле 3.8 определим наращенную сумму
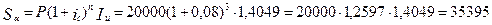 руб.
руб.
Ответ: наращенная сумма с учётом инфляции составит 35395 руб.
Вопросы для самопроверки
1. Сформулируйте понятие финансовая политика предприятия.
2. Назовите основные типы задач, решаемых финансовой политикой.
3. В чём состоят отличия управленческого подхода к классификации видов финансовой политики от бухгалтерского подхода?
4. Назовите типы целей деятельности предприятия.
5. Сформулируйте более правильный способ выбора лучшего варианта финансовой политики предприятия.
6. Дайте определение эквивалентной процентной ставки.
7. Что означает понятие «простая годовая процентная ставка эквивалентная простой годовой учётной ставке»?
8. Какая ставка сложных процентов называется «эффективной»?
9. Чем различаются понятия «темп инфляции» и «индекс инфляции»?
10. Чему равен индекс инфляции за год, если цены за каждые полгода растут на 10%?
[1] Когденко Вера Геннадьевна Краткосрочная и долгосрочная финансовая политика. –М.: ЮНИТИ-ДАНА, 2010.
Не нашли, что искали? Воспользуйтесь поиском: