Главная

Популярная публикация

Научная публикация

Случайная публикация

Обратная связь

ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Урок в 5 классе «Треугольник».

⇐ Предыдущая12



Основные элементы урока (план урока).

  1. Этап ознакомления учащихся с новым материалом
  2. Этап закрепления изученного на уроке
  3. Этап постановки задания на дом.

Цель урока. Систематизировать знания о треугольнике, решение задач.

Задачи.

1) Проверить знания, умения и навыки учащихся по изучаемому материалу за 1-4 классы.

2) Сформулировать понятие треугольника, его основных элементов (сторона, вершина, угол).

3) Закрепить изученный материал: решение различного вида задач.

Инструменты. Линейка, чертежный угольник.

Тип урока. Урок объяснения нового материала.

Форма организации работы на уроке. Фронтальная (коллективная).

Ход урока:

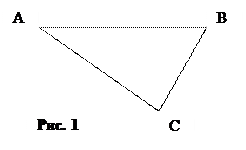Сегодня на уроке мы будем изучать геометрическую фигуру, которая называется треугольником. Все мы с таким понятием встречались с раннего детства, давайте рассмотрим такую ситуацию: представим себе дом в котором живет Петя, на доске дом обозначим точкой А(дом), школу в которую ходит Петя обозначим точкой В(школа), а магазин точкой С(магазин). Пусть эти точки не лежат на одной линии. Каждый день Петя выходит из дома и идет в школу. Как известно, самый короткий путь по прямой, значит путь от дома до школы мы обозначим отрезком АВ, т.е. соединяем А и В по прямой. После занятий в школе Петя решил зайти в ближайший магазин и купить чего-нибудь вкусного. Теперь мы можем с помощью линейки соединить точки В и С. После магазина Петя отправляется домой, значит, соединяем точки С и А. Итак весь путь Пети изображает геометрическую фигуру. Как вы думаете какую? Да, эта фигура и будет называться треугольником.

Давайте рассмотрим следующие рисунки на доске:

Что общего имеют эти рисунки?

Таким образом, рассмотренные рисунки имеют общий элемент – треугольник.

А теперь давайте найдем в классе что-нибудь похожее на этот элемент. Назовите предметы такого же вида, как на рисунке, где вы их встречали: дома, на пути в школу, на улице?

Поработаем в тетрадях: с помощью линейки начертите треугольник, у которого все стороны имеют различную длину.

Вводятся обозначения, чтение, основные элементы, периметр треугольника

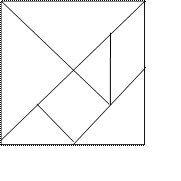Поработаем теперь устно. На доске изображен рисунок, сколько треугольников вы на нем видите?

Правильный ответ: 7 штук

Работаем в тетрадях. Начертите треугольник и обозначьте его АВС, с помощью линейки измерьте длины его сторон. Сравните длину какой-либо его стороны с суммой длин других его сторон. Какой можно сделать вывод?

рис 3.
Вывод. В треугольнике АВС сумма длин двух его сторон всегда больше длины третьей стороны.

Решаем задачи (учебник Н.Я. Виленкин).

 

№ 631. Измерьте, с помощью линейки и транспортира, стороны и углы по рисунку.

 

Вычислите их периметр и сумму углов

 

 

№ 632. Земельный участок прямоугольной формы имеет периметр 1750 м одна из его сторон 560 м, другая 780 м. Вычислить длину третьей стороны.

№ 633. Одна сторона треугольника 54 см, другая 68 см, а третья короче второй на 23 см. Вычислить периметр треугольника.

Задание на дом. Принести из дома предметы, имеющие треугольную форму, начертить в тетрадях различные треугольники:

а) треугольник с двумя равными сторонами;

б) треугольник, у которого все стороны равны;

в) треугольник, у которого один угол равен 900;

г) треугольник, у которого все углы по 600;

д) треугольник, у которого один угол равен 1200.

№ 634. Одна сторона треугольника 36 дм, другая а дм, а третья в дм. Доставь выражение дм, найди периметр треугольника и вычисли его, если а = 42, в = 51.

4. Осень 2002 г. внимание педагогической общественности вновь оказалось приковано к проблеме стандартизации образования. Это было вызвано публикацией нового проекта образовательного стандарта – «Федеральный компонент государственного образовательного стандарта общего образования». Здесь по сравнению с ранее разработанным проектом в обязательный минимум геометрической подготовки учащихся основной школы сделан был решительный шаг в сторону увеличения в ней сведений о пространственных фигурах.

Более широкое проникновение сведений о пространственных фигурах объясняется тем, что последнее время большое распространение получают курсы геометрии «основанные на взаимосвязанном обучении» свойств плоских и пространственных фигур. Данная тенденция представлена целым рядом учебных пособий и научно-методических разработок. Например.

· В.А. Панчищина «Геометрия для младших школьников»;

· В.А. Гусев «Геометрия 5-6 класс» - экспериментальный учебник;

· Д.Р. Дорофеев «Математика для 5-6 классов».

Но вызывает некоторую обеспокоенность то, что с точки зрения предлагаемых проектов учебного стандарта, не ясна судьба изучения геометрии в 5-6 классах. Опыт экспериментальной работы по данным учебным пособиям показывает, что на этапе 5-6 класс могут быть включены в содержание курса геометрии и полноценно усвоены учащимися вопросы геометрии пространства. Простейшие виды многогранников и тел вращения, их изображение, элементы, развертки, некоторые виды сечений пространственных фигур плоскостью, нахождение объемов некоторых пространственных фигур.

В условиях всеобщей стандартизации, содержание образования продиктовано программой для общеобразовательных школ, гимназий, лицеев, одобренной Департаментом общего среднего образования Министерства образования Российской Федерации, к которой мы сейчас обратимся:

Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике в школе:

  • овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
  • индустриальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
  • формирование представлений об идеях и методах математики, о математике как о форме описания и методе познания действительности;
  • формирование представлений о математике как о части человеческой культуры, понимания значимости математики для общественного прогресса.

Образовательные и воспитательные задачи обучения математике должны решаться комплексно с учетом возрастных особенностей учащихся, специфики математики как науки и учебного предмета, определяющей ее роль и место в общей системе школьного обучения и воспитания. Учителю предоставляется право самостоятельного выбора методических путей и приемов решения этих задач.

Обратимся теперь к структуре программы. Программа по математике для общеобразовательных учреждений состоит из трех разделов: «Требования к математической подготовке учащихся», «Содержание обучения», «Тематическое планирование учебного материала».

Раздел «Требования к математической подготовке учащихся» определяет итоговый уровень умений и навыков, которыми учащиеся должны овладеть по окончании основной и старшей школы. Требования распределены по основным содержательным линиям курса и характеризуют тот безусловный минимум, которого должны достигать все учащиеся.

Раздел «Содержание обучения» задает минимальный объем материала, обязательный для изучения в школе. Содержание здесь распределено не в соответствии с порядком изложения, принятым в том или иным учебнике, а по ступеням обучения и основным содержательным линям, объединяющим связанные между собой вопросы. Это позволяет учителю, отвлекаясь от места конкретной темы в курсе, оценить ее значение по отношению к соответствующей содержательной линии, правильно определить и расставить акценты в обучении, организовать итоговое повторение материала.

В разделе «Тематическое планирование учебного материала»приводится конкретное планирование, ориентированное на действующие в настоящее время учебники математики. При организации учебного процесса учителю следует строить свою работу, опираясь именно на раздел программы.

В программе представлены все геометрические фигуры:

- точка, прямая, луч, отрезок;

- угол: прямой, острый, тупой, градусная мера угла;

- треугольник, виды треугольников, периметр, площадь, пространственные фигуры: куб, параллелепипед, шар, конус, цилиндр.

5. Роль пропедевтического курса в современной геометрии.

· Учебник А.Д. Александров, А.Л. Вернер, В.И. Рыжик «Геометрия»

· В.А. Гусев «Я в пространстве»

· В.А. Смирнов «Курс для разных профилей»

Возраст с 6-12 лет – сенситивный период (для развития пространственного мышления).

В системном курсе геометрии информация представлена в виде логической структуры (дедуктивный курс), т.е. есть своя аксиоматика, теоремы, доказательства, системы задач.

Изучение систематического курса геометрии начинается в том возрасте, когда база для усвоения, понимания и осознания понятий уже сформирована.

Идея начального обучения элементарной геометрии не нова.

Я. А. Каменский и И.Г. Песталоцци выдвинули идею об обучении детей 6-12 лет элементарной геометрии, при этом они опирались на принцип наглядности, придали обучению развивающий характер.

В ХХ в. в 50-е годы появляется масса разнообразных исследований по педагогике и психологии (Л.С. Выготский, Б.Г. Ананьев, Пиаже). В основе обучения психология.

Карасев, А.М. Пышкало внесли значительный вклад в разработку курса по наглядно-практической геометрии.

Карасев «Элементы наглядной геометрии».

М. Н. Вески «Методика геометрии».

А.М. Пышкало предлагает методику формирования геометрических представлений и понятий.

На современном этапе:

Элементы пропедевтического курса геометрии в учебниках математики:

1) «Математика, 5», «Математика, 6»Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.

2) «Математика, 5», «Математика, 6» под ред. Г.В. Дорофеева, И.Ф. Шарыгина.

Пропедевтические курсы:

3) В.А. Гусев для 5-6 классов.

4) Г.А. Клековкин «Геометрия».

5) В.А. Панчищина «Геометия для младших школьников».

6) Н.С. Подходова «Геометрия в пространстве».

7) Т.Г. Ходот и др.

8) И.Ф. Шарыгин, Л.Н. Ерганжиева.

В.А. Гусев.

Цель курса. Формирование у учащихся общей картины мира, предоставление школьникам возможности его познания с использованием геометрических знаний

Материал курса развивает представления школьников, полученные в начальной школе.

Задачи курса. Показать как геометрия помогает познавать окружающий мир, как с помощью геометрии понять его закономерности, как использовать геометрию в практической жизни.

В учебнике Гусева В.А. «Я в пространстве», основная методическая линия – взаимосвязанное изучение свойств плоских и пространственных фигур. Плоские фигуры изучаются не сами по себе, а как части пространства. Раздельное изучение фигур на плоскости и в пространстве, не позволяет ученику увидеть общие закономерности геометрии. Учебник построен на дискуссии. Приведены 6 групп задач:

1. задачи вопросы (проверка усвоения);

2. стандартные (простые);

3. учебные (переходный этап);

4. творческие;

5. исследовательские (после изучения нескольких тем);

6. задачи для самостоятельного контроля.

Много знаний из практики. Автор постоянно соотносит геометрические факты с реальностью.

В курсе прослеживается пропедевтика и развитие пространственных представлений учащихся.

Г.А. Клековкин «Геометрия».

Те же идеи, что и у Гусева. Курс носит наглядный практический характер.

В.А. Панчищина «Геометрия для младших школьников».

Цель курса. Данная программа направлена на зарождение, накопление, осмысление, некоторую систематизацию геометрической информации.

Создается запас геометрических представлений, который в дальнейшем обеспечит основу для формирования геометрических понятий, идей, методов; максимально разовьет познавательные способности детей.

Тематические блоки:

1) Геометрические фигуры.

2) Путешествие по каменной летописи века (включая готику, древнюю Русь и современную архитектуру).

3) Конструкции: шашки, кубики.

4) Координаты и фигуры.

5) Симметрия.

6) Геометрические величины (V,S и т.д.).

7) Фигуры на экране компьютера: тангран.

Возможные варианты изучения курса:

с 4 по 6 класс,

с 4 по 5 класс.

Н.С. Подходова «Геометрия в пространстве».

Цель курса. Развитие пространственного мышления и рассмотрение окружающего мира с геометрической позиции на основе опыта ребенка.

В содержание включаются материал, связанный с разнообразными областями культуры и природы. Есть задания, направленные на развитие многозначного видения; задания, решаемые разными способами и мотивационные задания.

Структура изучения геометрии:

1) 1-3 класс. Сюжетная дидактическая игра, в процессе которой дети знакомятся с геометрическими формами и плоскими пространствами.

2) 5-6 класс. Наглядный курс. Построена в логике дедуктивного. Основана на конструировании.

3) 7-9 класс. Дедуктивный курс планиметрии с элементами стереометрии.

Возможные варианты построения курса геометрии:

1. а) изучение планиметрии;

б) изучение стереометрии.

2. Планиметрия с элементами стереометрии.

3. Узеонинский курс (идея совместного изучения планиметрии и стереометрии).

4) 10-11 класс. Дедуктивный курс. Углубление знаний по планиметрии на базе решения соответствующих задач.

Т.Г. Ходот

В 5-6 классе следует предоставить ребенку возможность, познакомится с тем, как устроены геометрические фигуры.

Вовлечь в конструирование, рисование, включить в процесс познания их свойства.

Все содержание курса и способ изложения предмета должны опираться на предыдущий опыт ребенка. При этом основой для всего курса – единая система визуальной поддержки.

Вся логика пропедевтического курса должна быть приближена к логике систематического курса.

Большое внимание следует уделять развитию речи ребенка, работе с терминами, формулировками определений.

Система заданий, упражнений должна с одной стороны знакомить детей с навыками проведения простейших логических операций.

Учебник хорошо иллюстрирован, много фотографий, рисунков. Задания выделены блоками.

И.Ф. Шарыгин.

Этапы обучения в школе:

1) Начальный этап (в начальной школе).

2) В средней школе.

3) В основной школе.

Эклектичность – смешение стилей

Ученика необходимо познакомить с различными точками зрения, чтобы ребенок имел возможность самостоятельно выбрать то, что ему нравится.

По направлениям:

1) Знакомство со свойствами простейших геометрических фигур.

2) Выработка навыков по изображению этих фигур.

3) Развитие геометрической интуиции

⇐ Предыдущая12




Не нашли, что искали? Воспользуйтесь поиском:
vikidalka.ru - 2015-2025 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных