
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Логарифмическая функция
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) - данная запись будет обозначать логарифм b по основанию а.
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.
6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:
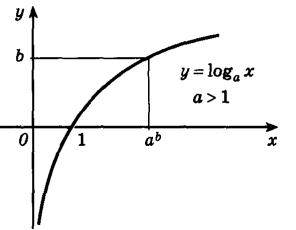
На следующем рисунке представлен график убывающей логарифмической функции - (0<a<1):
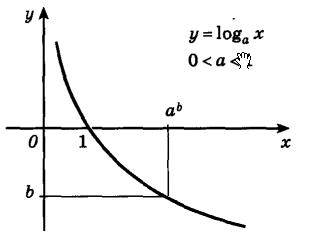
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.
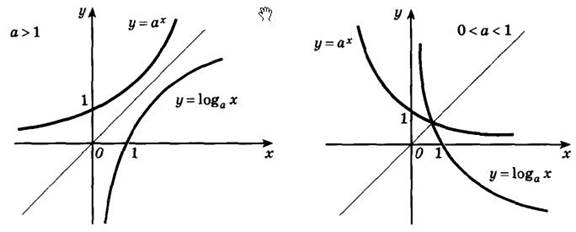
Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций. Рассмотрим пример: найти область определения логарифмической функции f(x) = log8(4 - 5*x).
Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 - 5*x>0. Решаем это неравенство и получаем x<0.8.
Таким образом, получается, что областью определения функции f(x) = log8(4 - 5*x) будет являться промежуток (-?;0.8)
Степенная функция
Функция y = xn называется степенной.
Показатель степени n принадлежит множеству действительных чисел.
График степенной функции при том, что n натуральное и n больше или равно двум называется параболой n-й степени. Если n четное, то функция y = xn является четной, её график симметричен относительно оси ординат. Чем больше четное n, тем круче поднимаются вверх ветви параболы:
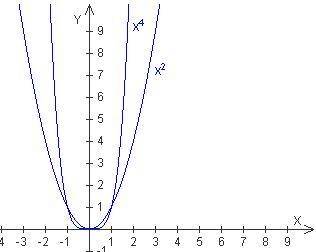
Степенная функция
Степенная функция с целым отрицательным показателем y = x-n, где n четное и больше или равно двум, является четной, её график симметричен относительно оси ординат. Пример для y = x-2
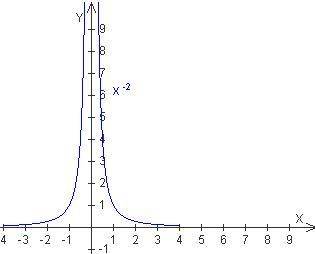
Степенная функция
Другой пример для y = x-4:
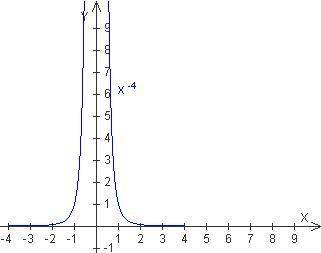
Степенная функция
Если n нечетное и n больше или равно трем, то функция y = xn является нечетной, её график симметричен относительно начала координат. Чем больше нечетное n, тем круче поднимаются вверх ветви параболы:

Степенная функция
Степенная функция с целым отрицательным показателем y = x-n, где n нечетное и больше или равно трем, является нечетной, её график симметричен относительно начала координат. Пример для y = x-3:
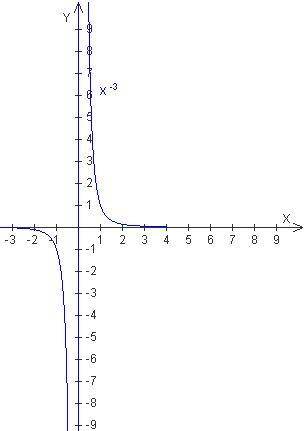
Не нашли, что искали? Воспользуйтесь поиском: