ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
б) систематическим влиянием пренебречь нельзя.
В этом случае составляют новый ряд, свободный от систематического влияния:
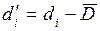, (15.7)
| где |  .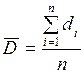
|
Формула (15.7) подобна формуле, по которой вычисляют уклонения от наиболее надежного значения:
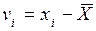. (15.8)
Сходство выражений (15.7) и (15.8) используют при выводе формул для оценки точности ряда двойных измерений.
II в случае, когда истинное значение измерявшейся величины неизвестно, для оценки точности используют уклонения от наиболее надежного значения, а среднюю квадратическую ошибку одного измерения определяют по формуле Бесселя:
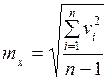. (15.9)
Аналогично для ряда, составленного по формуле (15.7), получим:
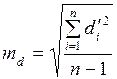. (15.10)
Точность каждого измерения характеризует средняя квадратическая ошибка, рассчитанная по формуле вида:
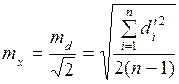. (15.11)
III точность наиболее надежных значений характеризует их средняя квадратическая ошибка, которую вычисляют по следующей формуле:
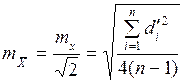. (15.12)
Воспользуемся изложенными выше выводами для обработки конкретного ряда двойных измерений. Ряд сформирован из результатов измерений десяти расстояний, каждое расстояние измерено дважды (2-я и 3-я колонки табл. 15.1), все измерения являются равноточными.
Таблица 15.1
| № | 
| 
| 
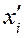
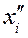
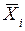
| di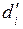, см |  , см
| 
| 
|
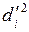
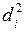
| 1075.640 | 1075.644 | 1075.642 | -0.4 | 1.4 | 1.96 | 0.16 | |
| 698.693 | 698.711 | 698.702 | -1.8 | 0.0 | 0.00 | 3.24 | |
| 896.342 | 896.309 | 896.326 | 3.3 | 5.1 | 26.01 | 10.89 | |
| 785.242 | 785.248 | 785.245 | -0.6 | 1.2 | 1.44 | 0.36 | |
| 951.197 | 951.250 | 951.224 | -5.3 | -3.5 | 12.25 | 28.09 | |
| 987.422 | 987.450 | 987.436 | -2.8 | -1.0 | 1.00 | 7.84 | |
| 778.445 | 778.471 | 778.458 | -2.6 | -0.8 | 0.64 | 6.76 | |
| 852.924 | 852.924 | 852.924 | 0.0 | 1.8 | 3.24 | 0.00 | |
| 1236.542 | 1236.591 | 1236.566 | -4.9 | -3.1 | 9.61 | 24.01 | |
| 654.269 | 654.301 | 654.285 | -3.2 | -1.4 | 1.96 | 10.24 | |
| Σ | – | – | – |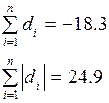 
| -0.3 | 58.11 | 91.59 |
Составим ряд разностей:
,
полученные значения занесем в 5-ый столбец табл. 15.1. Разности, учитывая их порядок, удобнее выразить в см.
Применим критерий (15.3) для обнаружения в величинах di остаточного систематического влияния:
.
Доверительную вероятность β примем равной 0.80, число степеней свободы: r= 10. Значение коэффициента tβ, выбранное из таблиц коэффициентов Стьюдента (Приложение 5), будет равно 1.4. В правой части неравенства (15.3) получим 13.8. Таким образом, отличие суммы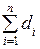 
от 0 превышает допустимое значение и не может считаться случайным. На основании условия (15.3) мы можем сделать вывод о наличии систематической составляющей в ряде разностей. Обработку ряда будем выполнять в порядке, изложенном для случая б).
I найдем наиболее надежные значения измеренных расстояний по формуле (15.1):
.
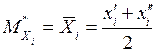Результаты занесем в 4-ую колонку табл. 15.1. В полученных числах сохраним порядок точности, который был в исходных данных.
II перейдем от разностей di к величинам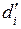 
, воспользовавшись формулой (15.7):
,
| где |  .
|
Значение 
будет содержать ошибку округления:
βокр. = 
окр.- =0.03.
Результаты запишем в 6-ой столбец нашей таблицы. Полученный таким образом ряд будет свободен от систематического влияния. Для вычисления средней квадратической ошибки одного измерения по формуле (15.11) величины 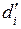необходимо возвести в квадрат, сохранив в числах на одну значащую цифру больше, чем в исходных данных (7-ая колонка табл. 15.1).
Отмеченное выше сходство между уклонениями от наиболее надежного значения и величинами 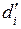может быть использовано для контроля правильности выполненных вычислений. Должны выполняться условия, аналогичные (14.5):
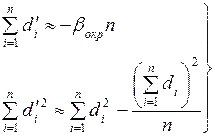(15.13)
Дополнительно потребуется вычислить квадраты разностей (8-ой столбец табл. 15.1). Подставив полученные значения в условия (15.13), получим:
.
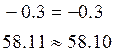Теперь можно приступать к вычислению средней квадратической ошибки одного измерения по формуле (15.11):
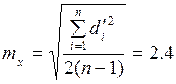см.
III для определения средней квадратической ошибки наиболее надежных значений воспользуемся формулой (15.12):
см.
Обработку ряда двойных равноточных измерений однородных величин можно считать завершенной: определены наиболее надежные значения измеренных расстояний, по ряду разностей выполнена оценка точности измерений и вычислений.
Приложение 5
Коэффициенты Стьюдента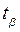 
|
 
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 0.95 | 0.98 | 0.99 | ||
| 0.16 | 0.33 | 0.51 | 0.73 | 1.00 | 1.38 | 2.0 | 3.1 | 6.3 | 12.7 | 31.8 | 63.7 | |||
| 0.82 | 1.06 | 1.3 | 1.9 | 2.9 | 4.3 | 7.0 | 9.9 | |||||||
| 0.98 | 1.3 | 1.6 | 2.4 | 3.2 | 4.5 | 5.8 | ||||||||
| 1.2 | 1.5 | 2.1 | 2.8 | 3.7 | 4.6 | |||||||||
| 1.2 | 1.5 | 2.0 | 2.6 | 3.4 | 4.0 | |||||||||
| 1.2 | 1.4 | 1.9 | 2.4 | 3.1 | 3.7 | |||||||||
| 1.1 | 1.4 | 1.9 | 2.4 | 3.0 | 3.5 | |||||||||
| 1.1 | 1.4 | 1.9 | 2.3 | 2.9 | 3.4 | |||||||||
| 1.1 | 1.4 | 1.8 | 2.3 | 2.8 | 3.3 | |||||||||
| 1.1 | 1.4 | 1.8 | 2.2 | 2.8 | 3.2 | |||||||||
| 1.1 | 1.4 | 1.8 | 2.2 | 2.7 | 3.1 | |||||||||
| 1.1 | 1.4 | 1.8 | 2.2 | 2.7 | 3.1 | |||||||||
| 1.1 | 1.4 | 1.8 | 2.2 | 2.7 | 3.0 | |||||||||
| 1.1 | 1.3 | 1.8 | 2.1 | 2.6 | 3.0 |
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Методические указания. Тема: «Использование техник правки текстов документов». |
Не нашли, что искали? Воспользуйтесь поиском: