Вихревое электрическое поле. Лекция 10. Теория и уравнения

Лекция 10. Теория и уравнения

Максвелла

План лекции

10.1. Вихревое электрическое поле.

10.2. Ток смещения.

10.3. Система уравнений Максвелла для электромагнитного поля.

Вихревое электрическое поле

Теория Максвелла¹ является единой и целостной теорией электрических и магнитных явлений в покоящихся средах. В основе теории лежат экспериментальные факты и законы, записанные математически, в общем виде, как система интегральных и дифференциальных уравнений Максвелла.

Первое уравнение описывает явление электромагнитной индукции. Из закона Фарадея известно, что в неподвижном контуре, при измерении сцеплённого с ним потока магнитной индукции возникает индукционный ток. Следовательно, в контуре появляются сторонние силы, вызывающие этот ток. Ни химические, ни тепловые процессы, ни сила Лоренца не могут быть причиной появления сторонних сил. Поэтому Максвелл предположил, что изменяющееся во времени магнитное поле порождает электрическое поле напряжённостью 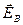, которая и вызывает появление индукционного тока в контуре. Наличие контура позволяет лишь обнаружить электрическое поле 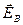по индукционному току.

Таким образом, изменяющееся во времени магнитное поле вызывает появление электрического поля напряжённостью 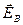, циркуляция которого по замкнутому контуру 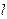, равна ЭДС индукции , но по закону Фарадея , равна скорости изменения магнитного потока , то есть:

, (10.1)

где - частная производная, которая учитывает зависимость потока магнитной индукции только от времени.

Поскольку контур и поверхность S неподвижны, операторы дифференцирования и интегрирования можно поменять местами, тогда уравнение Максвелла запишется в виде:

[1] Максвелл Д. К. (1831-1879), английский физик

. (10.2)

Для электростатического поля, созданного электрическим зарядом Q, циркуляция вектора напряжённости по замкнутому контуру 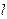, равна нулю:

.

Поэтому электростатическое поле является потенциальным и линии напряжения начинаются и заканчиваются на электрических зарядах. Электрическое поле 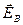принципиально отличается от поля . Его циркуляция в соответствии с (10.2) не равна нулю. Следовательно, электрическое поле, порождаемое изменяющимся магнитным полем, является вихревым и его линии напряжённости замкнуты.

Таким образом, электрическое поле может быть потенциальным, когда создаётся неподвижными зарядами и может быть вихревым, если создаётся изменяющимся во времени магнитным полем.

Ток смещения

Из рассмотренного выше явления электромагнитной индукции следует, что изменяющееся магнитное поле приводит к возникновению вихревого электрического поля. Максвелл предложил, что должно существовать и обратное явление, когда изменяющееся со временем электрическое поле должно вызывать появление магнитного поля в окружающем пространстве.

Так как магнитное поле всегда создаётся токами, то Максвелл назвал переменное электрическое поле возбуждающее магнитное, током смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 10.1).

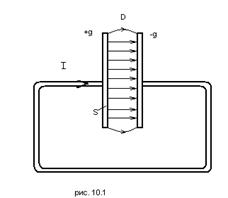
Ток проводимости течёт во всей цепи кроме пространства между обкладками конденсатора. В этом пространстве существует переменное электрическое поле, которое характеризует вектор электрического смещения . Максвелл предположил, что линии тока проводимости переходят непрерывно в линии тока смещения на границе обкладок конденсатора. Тогда плотность тока проводимости j равна плотности тока смещения: j _см = j. Вычислим j.

Вблизи от поверхности обкладок конденсатора плотность тока проводимости равна:

,

где - поверхностная плотность заряда, S – площадь обкладок конденсатора.

Тогда и плотность тока смещения также равна:

.

Электрическое смещение D между обкладками определяется по формуле:

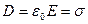, откуда

,

где - оператор частной производной, так как магнитное поле зависит только от быстроты изменения D во времени и .

Последнее равенство можно записать в векторном виде:

.

Ток смещения возникает при любом изменении электрического поля и существует не только в вакууме и диэлектриках, но и в проводниках, по которым течёт переменный ток. Поэтому Максвелл ввёл более общее понятие полного тока , равного сумме токов проводимости и смещения :

.

Силу полного тока , Максвелл записал в правую часть теоремы о циркуляции вектора и получил обобщённую теорему о циркуляции вектора , которая является вторым основным уравнением теории Максвелла:

Не нашли, что искали? Воспользуйтесь поиском: