Теорема Гаусса для электростатического поля в вакууме и ее применение к расчету электростатических полей

Из изложенного выше следует, что электростатическое поле любой конфигурации можно представить, как систему нескольких точечных зарядов и, используя соотношение (1.3, 1.9), рассчитать напряженность поля в любой его точке. Выполнение такой задачи существенно упрощается, если использовать теорему, выведенную К. Гауссом[2] (теорему Гаусса): поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную или в аналитической форме

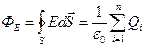, (1.9)

В качестве примера рассмотрим поле равномерно заряженной бесконечной плоскости (рис.1.3) с постоянной поверхностной плотностью зарядов " "

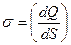, (1.10)

( – заряд, приходящийся на единицу площади).

Из соображений симметрии следует, что линии напряженности поля рассматриваемой плоскости перпендикулярны ей; направлены в обе стороны от нее и это поле однородно. В качестве произвольно замкнутой поверхности выберем цилиндр, поверхность основания которого площадью S параллельны плоскости, а образующие перпендикулярны ей. Запишем применительно к этой ситуации теорему Гаусса

(1.11)

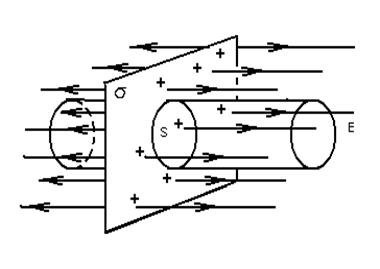
Рис.1.3

Полный поток вектора (число линий напряженности) сквозь поверхность цилиндра можно представить, как сумму потоков сквозь боковую поверхность и два основания, то есть

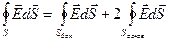(1.12)

Образующие цилиндра параллельны линиям вектора и значит

, так как , a .

Для оснований: ; 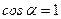и из (1.9 – 1.12) получим, учитывая, что поле однородно

; ; ,

и, окончательно

(1.13)

Отсюда следует, что напряженность рассматриваемого поля на любых расстояниях от плоскости одинакова по модулю, то есть поле действительно однородно. Опираясь на полученное соотношение (1.13), можно получить для поля двух параллельных разноименно заряженных плоскостей следующий результат. Суммарная напряженность в области между плоскостями

;

и, согласно (1.13),

. (1.13а)

Соответственно вне объема, ограниченного плоскостями поле отсутствует: .

К началу

Не нашли, что искали? Воспользуйтесь поиском: