Выберите задачу для решения из предложенных ниже.

1. Удалите из дерева все равные между собой элементы. В программе используйте подпрограммы.

2. Удалите из дерева все повторяющиеся элементы. В программе используйте подпрограммы.

3. Постройте два дерева. Проверьте, является ли одно из них поддеревом другого. Если "да", то удалите это поддерево. В программе используйте подпрограммы.

4. Постройте два дерева. Проверьте, является ли одно из них поддеревом другого. Если "нет", то включите это поддерево. В программе используйте подпрограммы.

5. Используя очередь или стек, вычислите среднее арифметическое всех элементов непустого дерева Т и удалите все элементы меньшие этого числа. В программе используйте подпрограммы.

6. Используя очередь или стек, поменяйте местами максимальный и минимальный элементы непустого дерева Т, все элементы которого различны. В программе используйте подпрограммы.

7. Используя очередь или стек, напечатайте все элементы дерева Т по уровням: сначала – из корня дерева, затем (слева направо) – из вершин, дочерних по отношению к корню, затем (также слева направо) – из вершин, дочерних по отношению к этим вершинам, и т.д. В программе используйте подпрограммы.

8. Используя очередь или стек, найдите в непустом дереве Т длину (число ветвей) пути от корня до ближайшей вершины с элементом Е. Если такого элемента не обнаружено, то выдайте на экран соответствующее сообщение. В программе используйте подпрограммы.

9. Используя очередь или стек, подсчитайте число вершин на n-ом уровне непустого дерева Т (корень считайте вершиной 0-го уровня). В программе используйте подпрограммы.

10. Объедините два дерева в одно идеально сбалансированное. В программе используйте подпрограммы.

Задачи для самостоятельного решения (на усмотрение учителя)

1. Напишите программу, содержащую процедуру или функцию, которая присваивает параметру Е элемент из самого левого листа непустого дерева (лист – вершина, из которой не выходит ни одной ветви), используя очередь или стек. В программе используйте подпрограммы.

2. Напишите программу, содержащую процедуру или функцию, которая находит в непустом дереве длины (число ветвей) путей от корня до всех вершин, используя очередь или стек. В программе используйте подпрограммы.

3. Напишите программу, содержащую процедуру или функцию, которая подсчитывает число вершин на каждом уровне непустого дерева (корень считать вершиной 0-го уровня). В программе используйте подпрограммы.

4. Напишите программу, содержащую процедуру или функцию, которая определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от еорня дерева до листьев. В программе используйте подпрограммы.

5. Напишите программу, содержащую процедуру, которая строит Т1 – копию дерева Т. В программе используйте подпрограммы.

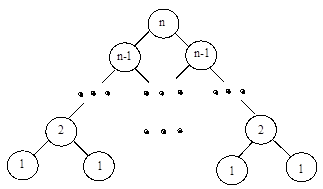
6. Напишите программу, содержащую процедуру Create(T,n), где n – положительное целое число, которая строит Т – дерево, изображенное на рисунке. В программе используйте подпрограммы.

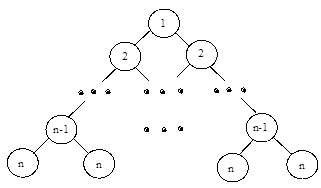
7. Напишите программу, содержащую процедуру Create(T,n), где n – положительное целое число, которая строит Т – дерево, изображенное на рисунке. В программе используйте подпрограммы.

8. Формулу вида

<формула>::=<терминал>|(<формула><знак><формула>)

<знак>::=+|-|*

<терминал>::=0|1|2|3|4|5|6|7|8|9

можно представить в виде двоичного дерева ("дерева-формулы") с элементами типа char согласно следующим правилам: формула из одного терминала (цифры) представляется деревом из одной вершины с этим терминалом, а формула вида (f1sf2) – деревом, в котором корень – это знак s, а левое и правое поддеревья – это соответствующие представления формул f1и f2. Для примера посмотрите как будет выглядеть дерево, соответствующее формуле (5*(3+8)).

Опишите рекурсивную функцию или процедуру, которая:

а) вычисляет (как целое число) значение дерева-формулы Т);

б) по формуле из текстового файла f строит соответствующее дерево-формулу Т;

в) печатает дерево-формулу Т в виде соответствующей формулы;

г) проверяет, является ли двоичное дерево Т деревом-формулой.

9. Пусть в дереве-формуле (см. предыдущую задачу) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Опишите процедуру, которая:

а) упрощает дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f+0), (0+f), (f-0), (f*1), (1*f) на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f*0) и (0*f), на вершину с 0;

б) преобразует дерево-формулу Т, заменяя в нем все поддеревья соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3) и (f1*(f2+f3), f1*(f2-f3)) на поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3)) и ((f1*f2)+(f1*f3), (f1*f2)-(f1*f3)).

10. Во внешнем текстовом файле записана (без ошибок) некоторая программа на языке Паскаль. Известно, что в этой программе каждый идентификатор (служебное слово или имя) содержит не более 9 латинских букв и/или цифр. Напечатайте в алфавитном порядке все различные идентификаторы этой программы, указав для каждого из них число его вхождений в текст программы. Необходимо учесть, что в идентификаторах одноименные прописные и строчные буквы отождествляются, что внутри литерных значений, строк-констант и комментариев последовательности из букв и цифр не являются идентификаторами и что в записи вещественных чисел может встретиться буква Е или е.

Стек

Не нашли, что искали? Воспользуйтесь поиском: