Частные производные высших порядков. Частные производные и функции z=f (x, y), вообще говоря, являются функциями переменных x и y

Частные производные и функции z=f (x, y), вообще говоря, являются функциями переменных x и y. Поэтому их можно снова дифференцировать по x и y. В результате получим четыре частные производные второго порядка, которые обозначаются так:

, , , .

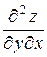Производные и 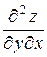называются смешанными. Если смешанная производная непрерывна при данных значениях x и y, то ее величина не зависит от порядка переменных, по которым берутся производные, т. е.

= .

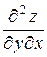Частные производные более высокого порядка определяются аналогично.

Пример 2. Найти частные производные второго порядка от функции

z=x ³ -2 x ² y + 3 y ² -5 xy.

Решение:

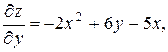
4. Касательная плоскость и нормаль к поверхности

Определение 4. Касательной плоскостью к поверхности в точке называется плоскость, в которой лежат все касательные к линиям, проходящим по поверхности через данную точку.

Определение 5. Прямая, перпендикулярная к касательной плоскости в точке касания, называется нормалью к поверхности в этой точке.

Если z=f (x, y) есть уравнение поверхности, то уравнения касательной плоскости и нормали к ней в точке имеют соответственно вид

(1)

(2)

Здесь и – значения частных производных при x=x ₀, y=y ₀.

Если поверхность задана уравнением F (x, y, z) = 0, то касательная плоскость к поверхности в точке определяется уравнением

(3)

а уравнения нормали –

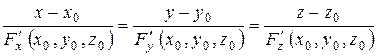. (4)

Пример 3. Написать уравнения касательной плоскости и нормали к поверхности z= 2 x ² + 4 y ² в точке М ₀(1; 2; 18).

Решение. 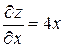; . При x =1, y =2 получим ; .

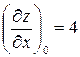По формуле (1) составим уравнение касательной плоскости

z -18 =4(x -1) + 16(y -2) или 4 x + 16 y - z -18 = 0;

уравнения нормали составим по формуле (2):

.

5. Экстремумы функции двух переменных

Определение 6. Точка P ₀(x ₀, y ₀) называется точкой максимума (или минимума) функции z=f (x, y), если для всех точек P (x, y), достаточно близких к точке P ₀ и отличных от нее, выполняется условие

f (x ₀, y ₀) > f (x, y) (или f (x ₀, y ₀) < f (x, y)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – экстремумами функции или экстремальными.

Теорема 1. (Необходимое условие экстремума). Если в точке P ₀(x ₀, y ₀) функция z=f (x, y) достигает экстремума, то в этой точке ее частные производные равны нулю или не существуют.

Точки, в которых частные производные и равны нулю или не существуют, называются критическими.

Необходимое условие экстремума не является достаточным, т. е. из него не следует, что в критической точке обязательно существует экстремум. Для исследования функции в критических точках используют достаточные условия.

Теорема 2. (Достаточные условия экстремума). Пусть точка P ₀(x ₀, y ₀) является критической точкой функции z=f (x, y), в которой и , и пусть в этой точке функция имеет непрерывные частные производные второго порядка

, , .

Тогда при x = x ₀, y = y ₀:

1) f (x, y) имеет максимум, если АС-В ² > 0 и А < 0;

2) f (x, y) имеет минимум, если АС-В ² > 0 и А > 0;

3) f (x, y) не имеет ни максимума, ни минимума, если АС-В ² < 0;

4) если АС-В ² = 0, то экстремум может быть и может не быть и требуется дополнительное исследование.

6. Производная по направлению. Градиент

Пусть даны точки М (x, y) и М ₁(x + Δ x, y + Δ y) и пусть вектор задает некоторое направление .

Определение 7. Производной функции z=f (x, y) в точке М (x, y) по направлению называется предел, обозначаемый и равный

, где .

Теорема 3. Если функция z=f (x, y) дифференцируема в точке М (x, y), то существует производная в этой точке по любому направлению и справедлива формула

, (5)

где cosα и cosβ – направляющие косинусы вектора .

Определение 8. Градиентом функции z=f (x, y) в точке М (x, y) называется вектор, координаты которого равны частным производным функции в этой точке:

. (6)

В направлении градиента скорость возрастания функции наибольшая и равна |grad z |.

Для функции u = f (x, y, z) производная по направлению и grad u в точке М (x, y, z) вычисляются по формулам:

,

Здесь cosα, cosβ, cosγ – направляющие косинусы вектора .

.

Решение типового варианта

Задача 1. Проверить, удовлетворяет ли уравнению

функция .

Решение. Находим

.

Дифференцируя повторно, получим

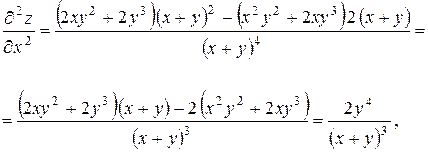
Подставим полученные выражения в левую часть уравнения:

Получаем тождество, т. е. функция z удовлетворяет данному уравнению.

Задача 2. Найти уравнения касательной плоскости и нормали к поверхности в точке М ₀(1; 2; -1).

Решение. Найдем частные производные функции 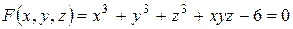и вычислим их значения в точке М ₀:

Подставляя их в уравнения (3) и (4) получим соответственно уравнение касательной плоскости

или

и канонические уравнения нормали

Задача 3. Найти экстремумы функции .

Решение. Находим

.

По необходимому условию экстремума критические точки найдем из системы

Получаем x =0, y =3, М ₀(0; 3).

Вычислим частные производные второго порядка в точке М ₀:

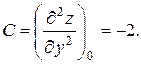
Так как AC - B ² = 3>0 и A<0, то согласно достаточным условиям экстремума в точке М ₀ функция имеет максимум и .

Задача 4. Даны функция z =5 x ² –3 x – y –1 и точки А (2; 1), В (5; 5). Найти в точке А и производную по направлению в точке А.

Вычислим значения частных производных функции в точке А:

Найдем по формуле (6):

=17 - .

Определим координаты вектора :

,

здесь x ₁, y ₁ – координаты точки А, x ₂, y ₂ – координаты точки B.

Длина вектора равна

,

а направляющие косинусы

,

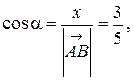
По формуле (5) вычислим производную по направлению :

Не нашли, что искали? Воспользуйтесь поиском: