ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

ТЕМА 7. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

1. Многомерные пространства.
2. Функции двух, трех и n переменных.
3. Линии уровня и поверхности уровня.
4. Понятие области. Открытая и замкнутая область.
5. Предел функции нескольких переменных.
6. Непрерывность функции нескольких переменных.
7. Свойства функций, непрерывных в ограниченной замкнутой области.

Функции одной переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.

В курсе средней школы уже рассматривались функции двух и трех переменных.

Например:

1) площадь S прямоугольника есть функция двух независимо друг от друга изменяющихся переменных – сторон прямоугольника a и b: S = ab;

2) объем V прямоугольного параллелепипеда – функция трех переменных – ребер параллелепипеда a,b,c: V = abc;

3) работа A электрического тока на участке цепи зависит от разности потенциалов Uна концах участка, силы тока I и времени t; эта функциональная зависимость задается формулой A = IUt.

Вопрос 1. Многомерные пространства

О.1.1. Упорядоченная совокупность n действительных чисел х₁, х₂, …, х_n называется n-мерным арифметическим вектором и обозначается х = (х₁, х₂, …, х_n). Числа х₁, х₂, …, х_nÎR называются компонентами вектора х.

Пусть х = (х₁, х₂, …, х_n) и у = (у₁, у₂, …, у_n). Введем операции сложения арифметических векторов и умножения их на действительные числа:

1) х + у = (х₁ + у₁, х₂ + у₂, …, х_n + у_n);

2) aх = (aх₁, aх₂, …, aх_n), aÎR.

О.1.2. Множество всех n-мерных арифметических векторов, в котором введены указанные выше операции сложения векторов и умножения их на действительные числа, называется n-мерным арифметическим векторным пространством или просто арифметическим пространством и обозначается Rⁿ.

Зададим в пространстве Rⁿ скалярное произведение векторов х и у с помощью формулы

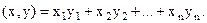(1)

Определим расстояние r(х,у) между элементами х и у пространства Rⁿ по формуле

(2)

Элементы пространства Rⁿ можно рассматривать и как n-мерные векторы, и как точки.

О.1.3. n-мерное арифметическое векторное пространство Rⁿ, в котором введено скалярное произведение векторов по формуле (1) и определено расстояние между элементами по формуле (2), называется точечным n-мерным арифметическим евклидовым пространством и так же обозначается Rⁿ.

Элементы данного пространства называются точками. Обозначение: М(х₁, х₂, …, х_n).

Точка О(0, 0, …, 0) называется началом координат пространства Rⁿ.

Вопрос 2. Функции двух, трех и n переменных

Пусть DÌ Rⁿ.

О.2.1. Если каждому элементу (х₁, х₂, …, х_n)ÎD по некоторому правилу f ставится в соответствие вполне определенное единственное число zÎR, то говорят, что на множестве D задана функция n переменных х₁, х₂, …, х_n, принимающая значения во множестве R:

z = f(х₁, х₂, …, х_n).

Переменные х₁, х₂, …, х_n - независимые переменные или аргументы; z - зависимая переменная или функция.

О.2.2. Множество D значений независимых переменных называется областью определения функции и обозначается D(z) или D(f). Множество значений, принимаемых z в области определения, называется областью значений функции и обозначается E(z) или E(f).

Далее, для простоты изложения, будем рассматривать только функции двух или трех переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных.

Обозначения: функция двух переменных - z = f(x,y);

функция трех переменных -u = f(x,y,z).

Областью определения функции двух переменных z = f(x,y) является подмножество точек координатной плоскости Оху, а областью определения функции трех переменных u = f(x,y,z) – подмножество точек пространства Oxyz.

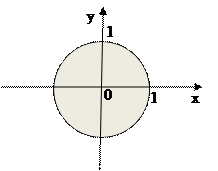
Пример. Найти область определения функции

Решение

- это круг с центром в начале координат и радиусом R = 1.

Функции двух переменных допускают графическую иллюстрацию.

0.2.3. Графиком функции z = f (x,y) называется множество точек пространства Oxyz с координатами (x,y,z), координаты которых удовлетворяют равенству z = f (x,y).

График функции z = f (x,y) представляет собой некоторую поверхность в трехмерном пространстве Oxyz. Для построения графика используется метод сечений, основанный на пересечении поверхности z = f (x,y) плоскостями, параллельными координатным плоскостям.

Способы задания функции двух переменных: табличный, аналитический, графический.

Вопрос 3. Линии уровня и поверхности уровня

В некоторых случаях можно получить наглядное геометрическое представление о характере изменения функции, рассматривая ее линии уровня или поверхности уровня, т.е. линии или поверхности, где данная функция сохраняет постоянное значение.

0.3.1. Линией уровня функции z = f (x,y) называется множество всех точек плоскости Oxy, в которых функция принимает одно и тоже значение C.

Таким образом, уравнение линии уровня имеет вид

f (x,y) = C,

где C - некоторая постоянная, называемая уровнем.

Очевидно, что при различных С получаются различные линии уровня данной функции.

Пример. Найти линии уровня функции z = x² + y².

Решение

x² + y² = C (C ≥ 0) – линиями уровня является семейство концентрических окружностей с центром в начале координат.

z = x² + y² - параболоид вращения (его проекции на плоскость Оху - окружности)

0.3.2. Поверхностью уровня функции u = f(x,y,z) называется множество всех точек пространства Oxyz, в которых функция принимает одно и тоже значение C.

Уравнение поверхности уровня имеет вид

f(x,y,z) = C.

Линии и поверхности уровня постоянно встречаются в физических процессах. Например, соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или с одинаковым средним суточным давлением, получим соответственно изотермы и изобары, являющиеся исходными данными для прогноза погоды. На топографических картах рисуют линии равной высоты над уровнем моря – горизонтали (линии уровня). По этой карте можно представить рельеф местности.

Вопрос 4. Понятие области. Открытая и замкнутая область

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной.

Введем понятие окрестности точки на плоскости (в R²). Пусть M₀(x₀,y₀)Î R².

О.4.1. δ-окрестностью точки M₀(x₀,y₀) называется множество всех точек M(x,y) плоскости Оху, координаты которых (х, у) удовлетворяют неравенству

или r(M,M₀) < d.

Обозначение: U(M₀,d).

U(M₀,d) ‒ все внутренние точки круга с центром в точке M₀(x₀,y₀) и радиусом δ.

О.4.2. Областью или открытой областью называется множество D всех точек плоскости, обладающих свойствами открытости и связности.

Свойство открытости: каждая точка области принадлежит ей вместе с некоторой окрестностью этой точки, т.е. является внутренней точкой области.

Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.

О.4.3. Точка M₀ называется граничной точкой области D, если любая окрестность этой точки содержит как точки области D, так и точки ей не принадлежащие.

О.4.4. Совокупность всех граничных точек области D называется ее границей.

О.4.5. Область D с присоединенной к ней границей называется замкнутой областью и обозначается

О.4.6. Область D называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса R. В противном случае область D называется неограниченной.

Пример. d- окрестность точки M₀(x₀,y₀) ‒ ограниченная область;

I-й координатный угол – неограниченная область.

О.4.7. Точка M₀ называется предельной точкой для области D, если в любой ее окрестности имеются точки области D, отличные от точки M₀.

Любая внутренняя или граничная точка области является предельной точкой для данной области.

Замечание

Все введенные понятия почти без изменения переносятся на пространство трех и большего числа измерений.

Вопрос 5. Предел функции нескольких переменных

Пусть функция z = f(x,y) определена в некоторой области D Ì R² и M₀(x₀,y₀) ‒ предельная точка для области D.

0.5.1. Число А называется пределом функции z = f(x,y) в точке M₀(x₀,y₀) (при x ® x₀ и y ® y₀), если для любого e > 0 существует число d = d(e) > 0 такое, что для всех точек M(x,y), удовлетворяющих неравенству 0 < r(M,M₀) < d, выполняется неравенство |f(x,y) ‒ A| < e.

Обозначение:

Пользуясь аналогией с функцией одной переменной, введем понятие бесконечно малой функции.

0.5.2. Функция z = f(x,y) называется бесконечно малой в точке M₀(x₀,y₀), если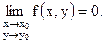

Все основные свойства о бесконечно малых и пределах, установленные для функции одной переменной, обобщаются и на случай нескольких переменных.

Пример.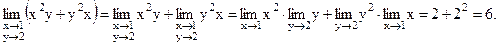

Замечание

Из определения 5.1 следует, что если предел существует, то он не зависит от пути, по которому точка М стремится к точке М₀ (число таких направлений на плоскости бесконечно в отличие от функции одной переменной, для которой х ® x₀ только в двух направлениях: справа или слева).

Пример. Доказать, что функция не имеет предела в точке О(0,0).

Решение

Будем приближаться к точке О(0,0) по прямым y = kx:

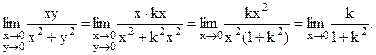
Очевидно, что значение предела зависит от величины углового коэффициента k прямой. Следовательно, предел не существует.

Вопрос 6. Непрерывность функции нескольких переменных

Пусть функция z = f(x,y) определена в точке M₀(x₀,y₀) и в некоторой её окрестности.

0.6.1. Функция z = f(x,y) называется непрерывной в точке M₀(x₀,y₀), если предел функции в этой точке существует и равен значению функции в этой точке, т.е._.

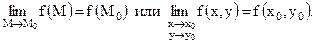
Геометрический смысл непрерывности функции двух переменных состоит в том, что ее график в точке М₀ представляет собой сплошную, не расслаивающуюся поверхность.

Можно дать другое, равносильное приведенному выше, определение непрерывности функции z = f(x,y) в точке.

Дадим аргументу х₀ приращение Dх, а аргументу у₀ ‒ приращение Dу, т.е. перейдем от точки M₀(x₀,y₀) к точке M(x₀ + Dх,y₀ + Dу). При этом функция z = f(x,y) изменится на величину

Dz = f(x₀ + Dх,y₀ + Dу) ‒ f(x₀,y₀),

которая называется полным приращением функции z = f(x,y) в точке M₀(x₀,y₀).

О.6.2. Функция z = f(x,y) называется непрерывной в точке M₀(x₀,y₀), если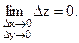

0.6.3. Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва данной функции.

Пример. Исследовать на непрерывность функцию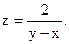

Решение

D(z): y ‒ x ¹ 0 Þ y = x ‒ линия разрыва данной функции (биссектриса I-го и III-го координатных углов). В точках данной прямой функция терпит разрыв.

Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям. Подобные теоремы имели место для функции одной переменной.

Вопрос 7. Свойства функций, непрерывных в ограниченной замкнутой области

О.7.1. Функция z = f(x,y) = f(M) называется непрерывной в некоторой области D, если она непрерывна в каждой точке данной области. При этом функция z = f(M) считается непрерывной в граничной точке M₀, если в равенстве точка M стремится к точке M₀ вдоль любого пути, принадлежащего данной области D.

Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной).

Справедлива теорема:

Т.7.1. (свойства функций, непрерывных в ограниченной замкнутой области)

Если функция z = f(M) непрерывна в ограниченной замкнутой области 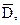то она в этой области:

1) ограничена, т.е. существует такое число K > 0, что для всех точек выполняется неравенство | f(M)| < K;

2) имеет точки, в которых принимает наименьшее значение и наибольшее значение;

3) принимает все промежуточные значения между любыми двумя своими значениями.

Замечание

Понятие предела, непрерывности и перечисленные свойства функций двух переменных легко обобщаются на функции трех и большего числа переменных.

Не нашли, что искали? Воспользуйтесь поиском: