Остовное дерево связного графа

Пусть G – некоторый связный граф. Дерево, множество вершин которого совпадает с множеством вершин графа G, а ребра являются ребрами графа G, называется остовным деревом графа G. Иными словами, остовное дерево графа G – это его подграф, содержащий все вершины и являющийся деревом.

Пример. На рис. 2 представлен граф с пятью вершинами и восемью ребрами. Четыре выделенные ребра (вместе с пятью вершинами) составляют остовное дерево этого графа. Остовное дерево определено неоднозначно.

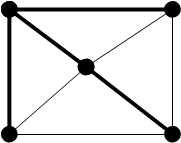
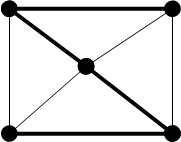Рис. 2

На рис. 3 выделены ребра, составляющие еще одно остовное дерево того же графа (заметим, что на этом рисунке невыделенные ребра также составляют остовное дерево).

Рис. 3

В прикладном плане задачу нахождения остовного дерева можно понимать как поиск системы связей между заданными точками без ненужного дублирования.

Построение остовного дерева. Остовное дерево T графа G можно сформировать следующим образом. Сначала берем в качестве T произвольную вершину графа G. Далее последовательно наращиваем дерево T в соответствии со следующим правилом: если на графе G имеется ребро, соединяющее вершины u и v такие, что u содержится в T, а v –

нет, добавляем к T это ребро вместе с вершиной v. Покажем, что при этом граф Т остается деревом. Во-первых, каждая добавляемая вершина связана с одной из уже входящих в T, так что добавление новых вершин и ребер оставляет граф T связным. Далее, в начальный момент граф T содержит одну вершину и не имеет ни одного ребра. Затем на каждом шаге построения число его вершин и число ребер увеличивается на единицу. Таким образом, число вершин графа T на единицу превосходит число его ребер. Следовательно, граф T является деревом. На некотором шаге дальнейшее расширение T окажется невозможным. Покажем, что в этом случае T представляет собой остовное дерево графа G, т.е. все вершины графа G попали в T. Обозначим через T ’ граф, который содержит все вершины графа G, не попавшие в T, и все соединяющие их ребра. На графе G нет ребер, которые имели бы одну концевую вершину в T, а другую в T ’. Так как граф G связный, T ’ не может быть непустым.

Пусть n – число вершин, а m – число ребер графа G. Любое его остовное дерево T имеет n вершин и n – 1 ребро. Таким образом, остовное дерево получается отбрасыванием m – n + 1 ребер графа G. Число (G) = m – n + 1 называют цикломатическим числом графа G.

Остовное дерево графа G может быть получено последовательным удалением (G) «лишних» ребер: на каждом

шаге можно отбросить любое ребро, если это не ведет к нарушению связности графа.

Предположим, что каждому ребру графа приписано некоторое положительное число, называемое его весом или стоимостью (это может быть, например, в случае информационных сетей, стоимость установления связи между концевыми точками). В этом случае граф называется нагруженным. Стоимостью нагруженного графа будем считать суммарную стоимость всех его ребер. Многие задачи, связанные с построением экономичных систем сообщения или информационных систем, приводят к задаче поиска остовного дерева минимальной стоимости.

Пусть G – связный нагруженный граф. Обозначим через c (T) стоимость произвольного подграфа T графа G. Если граф T связный, содержит все вершины графа G и имеет минимальную стоимость среди всех подграфов графа G, обладающих этими двумя свойствами, то T является остовным деревом. В самом деле, если бы граф T содержал цикл, то можно было бы отбросить, по крайней мере, одно ребро и тем самым уменьшить стоимость T.

Опишем алгоритм построения остовного дерева минимальной стоимости. Он получается небольшим видоизменением алгоритма построения остовного дерева связного графа. Сначала берем в качестве T вершину графа G, из которой выходит ребро минимальной стоимости. Далее, пока

это возможно, последовательно наращиваем дерево T: из всех ребер графа G, соединяющих вершины u ∈ T и v ∉ T, выбираем ребро минимальной стоимости и добавляем к T это ребро вместе с вершиной v. Полученное в результате исполнения этого алгоритма остовное дерево будет иметь минимальную стоимость.

Пример. На рис. 4 выделено остовное дерево минимальной стоимости. Его стоимость равна 6. Остовное дерево, представленное на рис. 2, при тех же оценках ребер имеет стоимость 8, остовное дерево на рис. 3 – стоимость 8, невыделенные ребра на рис. 3 составляют остовное дерево

стоимости 10.

3

1 2

3 3

2 1

Рис. 4

Не нашли, что искали? Воспользуйтесь поиском: