Ориентированные и упорядоченные деревья

Пусть G –дерево с n > 1 вершинами. Зафиксируем одну из вершин v 0 и назовем ее корнем. Выделение корня определяет на множестве вершин некоторое естественное отношение частичного порядка (ориентацию): вершина u предшествует вершине v (а вершина v следует за вершиной u), если u

встречается на пути из корневой вершины v 0 в вершину v. Если к тому же вершины u и v связаны дугой, то u называется непосредственно предшествующей вершине v (а v – непосредственно следующей за u). Говорят, что вершина v, удаленная на расстояние k от корневой вершины, расположена на уровне k (или является вершиной уровня k). Значение уровня согласуется с отношением порядка: если вершина u предшествует вершине v, то уровень u меньше уровня v. Обратное, вообще говоря, неверно. Представляя дерево графически, вершины обычно располагают так, чтобы значение уровня увеличивалось в направлении сверху вниз.

На рис. 5 представлено дерево, в котором вершина 0 является корнем; вершины 1 и 2 находятся на первом уровне, вершина 3 – на третьем; вершина 1 предшествует вершине 3; вершины 1 и 3 с вершиной 2 отношением предшествования не

связаны.

0

Рис. 5

Вершины, за которыми не следует ни одна вершина, называют концевыми, или, в «древесном» стиле, – листьями. На рис. 5 вершина 3 является листом, всего же дерево на этом

рисунке имеет 7 листьев. У деревьев с выделенным корнем вершины часто называют узлами. Неконцевые узлы называют узлами ветвления. Число вершин, непосредственно следующих за узлом ветвления, называют степенью ветвления этого узла. На рис 5 узлы 0 и 1 имеют степень ветвления 2, узел 2 – степень 3.

Каждую вершину дерева можно рассматривать как корневую вершину дерева, состоящего из всех следующих за ней вершин. Например, взяв в качестве корневых вершины 1 и 2

(см. рис 5), получим пару деревьев, изображенных на рис. 6.

1

2

Рис. 6

С учетом этого можно дать следующее рекурсивное определение дерева с корнем (или ориентированного дерева). Дерево с корнем T – это конечное множество, состоящее из одного или более узлов таких, что:

1) имеется один выделенный узел, называемый корнем данного дерева;

2) остальные узлы разбиты на m ≥ 0 попарно непересекающихся множеств, каждое из которых в свою очередь является деревом.

Например, дерево на рис. 7 можно описать следующим

образом:

T = {1, T 2}, T 2 = {2, T 3, T 4}, T 3 = {3, T 5, T 6, T 7},

T 5 = {5}, T 6 = {6}, T 7 = {7},

T 4 = {4, T 8}, T 8 = {8, T 9, T 10}, T 9 = {9}, T 10 = {10}.

В явном виде это описание выглядит так:

T = {1; {2; {3; {5}, {6}, {7}}, {4; {8; {9}, {10}}}}}.

1

3 2 4

5 6 7

9 10

Рис. 7

Если в рекурсивном определении ориентированного дерева считать существенным порядок, в котором перечисляются поддеревья, растущие из заданного корня, получается определение упорядоченного дерева. Например, дерево с рис. 7 можно представить как упорядоченное дерево

T = (1; (2; (3; (5, 6, 7)), (4; (8; (9, 10))))).

Возможно и иное представление. Например,

T ’ = (1; (2; (4; (8; (9, 10))), (3; (5, 6, 7)))).

Более формально:

1) всякий узел a является упорядоченным деревом с корнем a;

2) если a – некоторый узел, а T 1, T 1, …, Tm, m ≥0, – упорядоченные деревья, то T = (a; (T 1, T 1, …, Tm)) – упорядочен- ное дерево с корнем a.

Упорядоченные деревья – одна из наиболее распространен-

ных информационных и алгоритмических структур.

Например, дерево на рис. 8 задает алгоритм вычисления значения арифметического выражения (1+2) – (3/4)2.

+ –

^2

/

1 2

3 4

Рис. 8

Бинарные деревья

Бинарными называют упорядоченные деревья, в которых каждый узел имеет не более двух, непосредственно следующих

за ним узлов (рис. 9).

a

c b d

g e f

h i

Рис. 9

Бинарные деревья наиболее часто используются для представления информации, обрабатываемой с помощью вычислительных машин. Рекурсивно бинарное дерево можно определить как конечное множество узлов, которое или пусто, или состоит из корня и двух не имеющих общих узлов бинарных деревьев – левого и правого.

Приписывая дуге, ведущей из произвольного узла к левому дереву, символ «0», а дуге, ведущей к правому дереву, символ «1», можно любой путь из корневой вершины (а вместе с ним и конечную вершину этого пути) закодировать с помощью нулей и единиц.

Например, на рис. 9 корневая вершина a получает в качестве кода пустую последовательность ∅, а остальные вершины следующие коды:

b – 1; c – 10; e – 100; f – 101;

d – 11; g – 111; h – 1110; i – 1111.

Найдем число различных бинарных деревьев с заданным числом вершин.

Пусть bn – число различных бинарных деревьев с n вершинами. Ясно, что b 0 = 1 (имеется ровно одно пустое бинарное дерево) и b 1 = 1.

При n > 0 всякое бинарное дерево с n вершинами имеет вид (a; (T 0, T 1)), где T 0 – бинарное дерево с k < n вершинами, а T 1 – бинарное дерево с n – k – 1 вершиной. Число способов расположить одно бинарное дерево с k < n вершинами слева от

корня, а другое бинарное дерево с n – k – 1 вершиной справа от корня равно bkbn – k –1. Следовательно, суммируя по всем k < n,

получаем:

bn = b 0 bn –1 + b 1 bn –2 + … + bn –1 b 0. (1)

В частности:

b 1 = b 02 = 1; b 2 = b 0 b 1 + b 1 b 0 = 2;

b 3 = b 0 b 2 + b 1 b 1+ b 2 b 0 = 5; ….

Последние равенства показывают, что последовательность чисел (bn) – это последовательность чисел Каталана (см. 11.4).

Для полноты изложения напомним коротко, как могут быть

получены явные выражения в факториалах для чисел bn.

Запишем производящую функцию:

B (z) = b 0 + b 1 z + b 2 z 2 + …. (2)

Основываясь на (1), получаем:

B (z)2 = b 02 + (b 0 b 1 + b 1 b 0) z + (b 0 b 2 + b 1 b 1+ b 2 b 0) z 2 … =

= b 1 + b 2 z + b 3 z 2 + ….

Умножая обе части последнего равенства на z и добавляя 1,

приходим к соотношению

z ⋅ B (z)2 +1 = B (z).

Таким образом, y = B (z) удовлетворяет квадратному уравнению

z ⋅ y 2 – y +1 = 0.

Решая его, находим:

B (z) 

1 1−

2 z

1 − 4 z .

Теперь разложим правую часть полученного равенства,

воспользовавшись биномом Ньютона:

 1/ 2 

B (z) 

∑ (−1) k 

⋅22 n 1 zn.

n ≥0

 n 1

Сравнивая (1) и (2), приходим к заключению, что для всех n

справедливо следующее равенство:

 1/ 2 

1 2 n 

bn =

(−1) k 

⋅22 n 1 =

 . (3)

 n 1

n 1 n 

Пример. Перечислим все бинарные деревья с 4 вершинами.

В соответствии с формулой (3) имеем:

b  1 8  8⋅7 ⋅6⋅5

14.

 

4 5 4



5 ⋅ 4 ⋅ 3 ⋅ 2

 

На рис. 10, представлены четырнадцать бинарных деревьев с четырьмя вершинами.

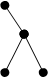
Рис. 10

Применим к (3) формулу Стирлинга. Получаем:

1 4р n ⋅(2 n)2 n e − 2 n

22 n

bn ≈

n  1

 2р n ⋅ n

ne − n 2

=

(n 1)

. (4)

р n

Формула (4) дает хорошее приближение даже при сравнительно малых значениях n. Например, при n = 4 имеем:

b 4 ≈

≈ 14,4.

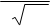4р

Не нашли, что искали? Воспользуйтесь поиском: