Властивості первісної

Суть методу

Якщо

— основна матриця системи,

— вектор-стовпчик вільних членів,

— вектор-стовпчик невідомих;

то має місце рівність:

Якщо матриця є квадратною та невиродженою, то для неї існує обернена матриця. Помноживши обидві частини рівняння зліва на , отримаємо

.

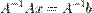оскільки та , то отримаємо формулу:

23) Поняття первісної та її властивості.

Функція зветься первісною функції на деякому інтервалі дійсних чисел, якщо — похідна функції на цьому інтервалі, тобто в усіх внутрішніх точках інтервалу виконується рівність

Можна довести, що у будь-якої неперервної на інтервалі функції існує первісна, яка також є неперервною функцією на цьому інтервалі.

Якщо — будь-яка первісна функція то , де C - довільна стала, — також первісна цієї функції і "невизначений інтеграл функції " посилається до множини яка складається з усіх первісних функції де — довільна константа.

Властивості первісної

• Первісна суми дорівнює сумі первісних
• Первісна твори константи та функції дорівнює добутку константи і первісної функції
• Достатньою умовою існування первісної у заданої на відрізку функції f є безперервність f на цьому відрізку
• Необхідними умовами існування є приналежність функції f першого класу Бера і виконання для неї властивості Дарбу
• У заданої на відрізку функції будь-які дві первісні відрізняються на постійну.

24)Невизначений інтеграл, його властивості. Табличні інтеграли. Основні методи інтегрування.

Дія знаходження невизначеного інтеграла називається невизначеним інтегруванням. Невизначене інтегрування є дією, оберненою до диференціювання.

За допомогою диференціювання ми за даною функцією знаходимо її похідну, а за допомогою невизначеного інтегрування ми за даною похідною функції знаходимо первісну функції.

Інтеграл від суми певного скінченого числа функцій дорівнює сумі інтегралів від цих функцій.

Сталий множник підінтегральної функції можна винести за знак інтеграла.

Похідна невизначеного інтеграла дорівнює підінтегральній функції.

Фігура, яка обмежена віссю абсцис, графіком заданої неперервної на проміжку [ a; b ] функції, що набуває на цьому проміжку лише невід’ємних значень, і вертикальними прямими, що проходять через кінці проміжка, називається криволінійною трапецією. Якщо F(x) –первісна заданої функції, то площа цієї криволінійної трапеції дорівнює приросту первісних функції на заданому проміжку, тобто різниці значень первісної в правому кінці проміжку і лівому кінці проміжку.

Якщо поділити заданий проміжок точками на рівні проміжки, провести через точки поділу вертикальні прямі, то задана криволінійна трапеція розіб’ється на криволінійні трапеції, які будуть мало відрізнятися від прямокутників, коли кількість частин, на які розбито заданий проміжок, прямує до нескінченності.

З теорії площ знаємо, що:

Площа фігури, складеної з декількох фігур, дорівнює сумі площ цих фігур. Площа прямокутника дорівнює добутку його вимірів.

Сума площ прямокутників, на які розіб’ється криволінійна трапеція, називається інтегральною сумою.

27) Диференціальні рівняння — розділ математики, який вивчає теорію та способи розв'язування рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні диференціальні) чи кількох аргументів (диференціальні рівняння в частинних похідних). Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів.

Теорія диференціальних рівнянь — розділ математики, що займається вивченням диференціальних рівнянь і пов'язаних з ними задач. Їх результати застосовуються в багатьох природничих науках, особливо широко — у фізиці.

Простіше кажучи, диференціальне рівняння — це рівняння, в якому невідомою величиною є деяка функція. При цьому, в самому рівнянні бере участь не тільки невідома функція, але й різні її похідні. Диференціальним рівнянням описується зв'язок між невідомою функцією та її похідними. Такі зв'язки віднаходяться в різних областях знань: у механіці, фізиці, хімії, біології, економіціта ін.

Розрізняють звичайні диференціальні рівняння і диференціальні рівняння з частинними похідними. Складнішими є інтегро-диференціальні рівняння.

Спочатку диференціальні рівняння виникли із задач механіки, в яких брали участь координати тіл, їхні швидкості та прискорення, розглянуті як функції від часу.

Диференційне рівняння називається інтегровним в квадратурах, якщо задачу знаходження усіх розв'язків можна звести до обчислення скінченного числа інтегралів від відомих функцій і простих алгебраїчних операцій.

Звичайні диференціальні рівняння

Звичайні диференціальні рівняння — це рівняння виду , де — невідома функція (можливо, вектор-функція; в такому випадку часто говорять про систему диференціальних рівнянь), що залежить від змінної часу , штрих означає диференціювання по . Число називається порядком диференціального рівняння.

Розв'язком (або рішенням) диференціального рівняння називається функція, що диференціюється n разів, і задовольняє рівнянню в усіх точках своєї області визначення. Зазвичай існує ціла множина таких функцій, і для вибору однієї з них на розв'язок потрібно накласти додаткові умови: наприклад, вимагати, щоб рішення приймало в певній точці певне значення.

Основні завдання і результати теорії диференціальних рівнянь: існування і єдиність рішення різних задач для ЗДР, методи розв'язання простих ЗДР, якісне дослідження рішень ЗДР без знаходження їхнього явного вигляду.

Задача Коші — одна з основних задач теорії диференціальних рівнянь полягає в пошуку розв'язку (інтеграла) диференціального рівняння, що задовольняє початковим умовам (початковим даним).

Задача Коші зазвичай виникає при аналізі процесів, обумовлених диференціальним законом і початковим станом, математичним виразом яких і є рівняння та початкова умова (звідси й термінологія та вибір позначень: початкові дані задаються при , а розв'язок знаходиться при ).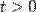

Від крайових задач задача Коші відрізняється тим, що область, в якій повинен бути визначений шуканий розв'язок, тут заздалегідь не вказується. Проте, задачу Коші можна розглядати як одну з крайових задач.

28) Числовий ряд - це числова послідовність, розглянута разом з іншою послідовністю, яка називається послідовністю часткових сум (ряду).

Замість нескінченного підсумовування, користуючись знаком суми, часто пишуть ∑

Поняття нескінченного ряду, це нове поняття, ми поки не вміємо визначати, чому дорівнює його сума.

Означення. N - ою частковою сумою ряду називається скінчена сума всіх членів ряду до n - ого члена включно, тобто сума

Означення. Числовий ряд називається збіжним, якщо існує скінчена границя послідовності його часткових сум

Якщо границя дорівнює нескінченності або не існує, то кажуть, що ряд розбігається.

1)Матриці. Дії над ними.

Матриця - це прямокутна таблиця, яка складена з деякої кількості рядків (або стовпців) однакової довжини.

Матриці записують слідуючим чином:

Кажуть, що матриця A є прямокутна матриця розміру (m n).

Якщо m=n, то A називається квадратною матрицею порядку n.

Числа aij називають елементами матриці, індекс i вказує на номер рядка, j на номер стовпця, на перетині яких розташований даний елемент.

Матриця, всі елементи якої дорівнюють нулю, називається нульовою. Позначають нуль-матрицю просто 0 (нуль).

Елементи квадратної матриці, які розташовані на перетині рядків та стовпців з однаковими номерами, складають головну діагональ квадратної матриці.

Якщо рядки матриці A записати стовпцями (у порядку слідування рядків матриці A), то таке перетворення називають транспонуванням матриці A. Транспоновану матрицю позначають AT.

Якщо довільна квадратна матриця A задовільняє умові AT=A, то така матриця називається
симетричною, якщо ж AT=−A, то - кососиметричною.

Нехай A=(aij) B=(bij) - матриці однакового розміру. Сумою цих матриць називається матриця A+B=C=(cij), де cij=aij+bij, тобто, дія додавання матриць виконується поелементно. Добутком матриці A=(aij) на число називається матриця A=( aij).

Добутком однієї матриці на другу є матриця, у якої елемент, розташований на перетині i-го
рядка та j-го стовпця, визначається як добуток i-го рядка першої матриці на j-тий стовпець другої.

Основні властивості операцій додавання матриць і множення матриці на число:
1. A+B=B+A (комутативність).

2. A+(B+C)=(A+B)+C (асоціативність).

3. A+0=A, при будь-якій матриці A.

4. Для будь-якої матриці A існує протилежна матриця (−A), така, що A+(−A)=0.

Властивості множення матриць:
1. ( A)B=A( B)= AB, де - число.

2. (A1+A2)B=A1B+A2B A(B1+B2)=AB1+AB2

3. A(BC)=(AB)C (асоціативність).

Множення матриць є некомутативною операцією.

Властивості операції транспонування:
1. (AT)T=A

2. (A+B)T=AT+BT

3. (AB)T=BTAT

2) Визначники другого, третього порядку. Властивості визначників.

Значення виразу

називають визначником (детермінантом) другого порядку.

називають визначником третього порядку.

Порядок визначника дорівнює числу його рядків (число стовпців співпадає з числом рядків).

Символи називають елементами визначника, причому перший індекс вказує номер рядка, а другий індекс – номер стовпця, на перетині яких стоїть даний елемент.

Властивості

1)Визначник змінить знак на протилежний, якщо переставити місцями два рядки (два стовпці).

2) Якщо всі елементи рядка (стовпця) дорівнюють нулю, то визначник дорівнює нулю.

3) Визначник з двома однаковими рядками (стовпцями) дорівнює нулю.

4). Спільний множник усіх елементів рядка (стовпця) можна винести за знак визначника.

5) Якщо елементи деякого рядка (стовпця) є сумою двох доданків, то визначник дорівнює сумі двох визначників

6). Якщо до елементів будь-якого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число, то значення визначника не зміниться.

5) метод Гауса

Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь. Початок алгоритму.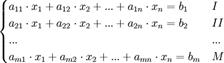

Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутного вигляду.

З цього моменту починається зворотний хід. З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок

4) метод Крамера

Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році.

Опис методу

Для системи лінійних рівнянь з невідомими (над довільним полем)

з визначником матриці системи , що не рівний нулю, розв'язок записується у такому вигляді:

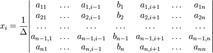
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).

Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c₁, c₂, …, c_n виконується рівність:

У такій формі формула Крамера справедлива без припущення, що не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори 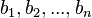та , або набір складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.

15) Взаємне розміщення двох прямих на площині. Кут між прямими. Умови перпендикулярності і паралельності.

Взаємне розміщення прямих на площині

Дві прямі на площині можуть:

• збігатися;

• бути паралельними (тобто не перетина­тися);

• мати одну спільну точку.

Нехай дві прямі і задані рівняннями

і . Позначимо через

і кути, які утворюють прямі і з додатнім напрямком осі (рис.3.8), а це кут між цими прямими.

Рис.3.8

Тоді а Оскільки, то

Якщо прямі і паралельні, то їх кутові коефіцієнти рівні

Якщо прямі перпендикулярні, то, а тому Можна обчислювати кут між двома прямими як кут між їх нормальними векторами і

6. обернена матриця

Обернена матриця — матриця (позначається ), яка існує для кожної невиродженої квадратної матриці , розмірності , причому:

де одинична матриця.

Якщо для матриці існує , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.

7) Вектор - це напрямлений відрізок або вектор - це паралельний перенос

Якщо початок і кінець співпадають, вектор називають нульовим або О Два вектори називають рівними, якщо їх довжини рівні, а напрями співпадають

Вектори, які лежать на паралельних прямих, називають колінеарними.

Вектори, які лежать в одній площині, називають компланарними

Сумою двох векторів і називається вектор, що є діагоналлю паралелограма, побудованого на даних векторах як на сторонах паралелограма

Щоб від вектора відняти вектор, треба до вектора додати вектор, або, що те саме, до вектора додати вектор з протилежним знаком.

В результаті множення вектора на скаляр одержується вектор, напрямок якого збігається з напрямком, якщо, і протилежний напрямку, якщо . Довжина одержаного вектора дорівнює

Ділення вектора на скаляр зводиться легко до множення вектора на скаляр

8) Гіпербола — крива другого порядку з ексцентриситетом більшим за одиницю. Гіпербола є невиродженою кривою другого порядку, яка задається рівнянням

де та 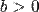— параметри. Таке рівняння називається канонічним рівнянням гіперболи.^[2]

Нехай канонічне рівняння кривої другого порядку шляхом переносу центру координат перетворено у вигляд: В цьому випадку крива проходить через початок координат нової системи; вісь абсцис є віссю симетрії кривої. Це рівняння відображає той факт, що невироджена крива другого порядку є геометричним місцем точок, відношення відстаней яких (ексцентриситет) від фокуса) та від заданої прямої незмінна. Крива є гіперболою, якщо . Тобто, гіпербола є геометричним місцем точок, абсолютна величина різниці відстаней яких від фокусів дорівнює Директоріальна властивість гіперболи полягає в тому, що гіпербола є геометричним місцем точок, відношення відстаней яких від фокуса до одноіменної директриси дорівнює Якщо в рівнянні гіперболи , то гіпербола називається рівнобічною. В координатах рівняння рівнобічної гіперболи матиме вигляд: звідки випливає, що по відношенню до координат та рівнобічна гіпербола представляє собою графік звортньо-пропорційної залежності. В координатах та маємо такий саме графік обернений на кут .

9) Пара́бола — геометричне місце точок, що рівновіддалені від точки і прямої. Одна з кривих другого порядку. Точка зветься фокусом, а пряма - директрисою. Парабола, гіпербола та еліпс є конічними перерізами. Парабола є конічним перерізом з одиничним ексцентриситетом.Якщо точкове джерело світла розміщене у фокусі параболоїдного дзеркала, то відбиті від поверхні промені будуть розповсюджуватися паралельно. Графік функції, що задається за допомогою поліному другого порядку від однієї змінної являє собою параболу.

Канонічне рівняння параболи в прямокутній системі координат:

(або , якщо поміняти місцями осі).

Квадратне рівняння при також представляє собою параболу і графічно зображаєтся тією ж параболою, що і 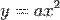, але на відміну від останньої має вершину не в початку координат, а в деякій точці , координати якої обчислюються за формулами:

Рівняння може бути представлено у вигляді 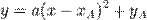, а у випадку переносу початку координат в точку канонічним рівнянням. Таким чином для кожного квадратного рівняння можна найти систему координат таку, що в цій системі воно представиться канонічним.\

10) Вектори в просторі.

Якщо вектор a, який знаходиться в прямокутній системі координат OXYZ, має початком точку A з координатами X_A, Y_A, Z_A, а кінцем – точку B з координатами X_B, Y_B, Z_B, то числа X_B - X_A, Y_B - Y_A, Z_B - Z_A називається його координатами: a(X_B - X_A; Y_B - Y_A; Z_B - Z_A).

Сумою векторів a(X_A; Y_A; Z_A) і b(X_B; Y_B; Z_B) називається вектор c(X_A + X_B; Y_A + Y_B; Z_A + Z_B).

Добутком вектора a(X_A; Y_A; Z_A) на число λ називається вектор λa(λX_A; λY_A; λZ_A).

Скалярним добутком векторів a та b, якщо відомі їх координати, є величина a•a = X_A•X_B + Y_A•Y_B + Z_A•Z_B.

12) Пряма і площина в просторі Умови перпендикулярності і паралельності

1. Дві площини називаються перпендикулярними, якщо двогранний кут між ними дорівнює 90 градусам. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.) Паралельними (рівнобіжними) прямими називають прямі, котрі лежать в одній площині і або збігаються, або не перетинаються. В деяких шкільних означеннях, щоправда, паралельні прямі не можуть збігатись, але тут цей факт не береться до уваги.

Властивості

1. Паралельність — Бінарне відношення еквівалентності, тому разбиває всю множину прямих на класи паралельних між собою.

2. Через довільну точку можна провести лише одну пряму, паралельную даній. Це властивість евклідової геометрії, в інших геометріях число 1 замінено іншими (в геометрії Лобачевского таких прямих минімум дві).

3. Дві паралельні прямі в просторі лежать в одній площині.

4. При перетині двох паралельних прямих третьою, т. зв. січною:

1. Січна обов'язково перетинає обидві прямі.

2. При перетині утворюється 8 кутів, при чому деякі характерні їх пари мають особливі назви та властивості:

1. Перехресні кути рівні.

2. Відповідні кути рівні.

3. Односторонні кути в сумі становлять 180°.

4. І, очевидно, суміжні кути в сумі становлять 180°, а вертикальні — рівні.

13)

Не нашли, что искали? Воспользуйтесь поиском: