
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Логарифм числа .Десятичный логарифм. Его свойства. Натуральный логарифм
Логарифм – показатель степени,в которую надо возвести в число «а», чтобы получить число «в».
Две операции обратные операции возведения в степень  = b
= b
1)  = b
= b
Действие,которое необходимо произвести, чтобы найти х = извлечение корня Х = 
2)  = b
= b
Действие, которое необходимо произвести, чтобы определить показатель степени, = нахождение логарифма числа b по основанию a
Свойство десятичных логарифмов:
1) Логарифм целого числа, изображенного как единица с послед. нулями, есть целое число равное числу нулей в избр числа
Lg10000000= 7
2) Логарифм десятичной дроби, изображенный как единица с предшествующими нулями,есть целое число равное количеству 0
Натуральный логарифм:
Натуральный логарифм – логарифм положительного числа M по основанию Е
10) Свойство логарифмов:
1) Отрицательные числа не имеют логарифмов (-м не сущест)
2)  = 1 a > 1; a ≠ 1
= 1 a > 1; a ≠ 1
Логарифмы чисел > 1 – положительны
Логарифмы чисел <1 – отрицательны
3) M > 1 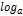 M > 0
M > 0
0 < M < 1  M < 0
M < 0
4) Большему числу соответствует больший логарифм (a > 1)
5) A > 0; a ≠ 1 M > 0; N > 0
a) 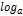 (M*N) =
(M*N) =  *M +
*M + 
б)  =
= 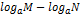
в) 
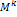 = k *
= k * 
6) Для любых чисел:
A > 0, a ≠ 1, M > 0 Выполняется соотношение: 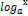 =
=  *
* 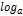 M
M
6) a > 0, a ≠ 1, M > 0
11) Логарифмическая функция. Свойства:
1) Область определения функции – множество всех чисел (0; +∞)
2) Область значения функции – множество всех действительных чисел (-∞;+∞)
A > 1
1)функция непрерывна и возрастает на промежутке (0; +∞)
2) если х стремится к +∞, то у тоже
3) если х стремится к 0, то у стремится к -∞
4) если 0 < x < 1, то y < 0
0 < a, 1
1) функция непрерывна и убывает на промежутке (0; -∞)
2) если х стремится к +∞, то у к -∞
3) Если х стремится к 0, то у стремится к +∞
4) Если x > 1, то у < 0
5) Если 0 < x < 1, то y > 0
12) Иррациональные уравнения, способы их решения:
- Называют уравнения,у которых неизвестная величина входит в подкоренное выражение.При решении иррационального уравнения необходимо учитывать:
А) если степень корня четное число, то подкоренное выражение должно быть больше или равно 0
Б) если степень корня нечетное число, то подкоренное выражение может быть любым действительным числом
Методы решения:
1) Возведение в одну и ту же степень обеих частей уравнения
2) Замена неизвестных
13) Показательные уравнения. Способы их решения:
Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени.
Способы:
1) приведение к одному основанию левой и правой частей, применяя свойства степеней:
2) метод вынесения общего множителя за скобки:
При решении неравенства такого типа применяется логарифмирование обеих частей неравенства по основанию а или b
14) Логарифмические уравнения. Способы их решения:
- такие уравнения, в которых неизвестная величина находится под знаком логарифма
А)  =
= 
Б) 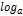 x =
x = 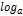 L, где L =
L, где L =  => x = L
=> x = L
15) Показательное неравенство. Методы их решения:
- называются неравенства содержащие переменные с показателем степени
Простейшими показательными неравенствами явл неравенства вида:

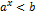 (a ≠ 1, a > 0)
(a ≠ 1, a > 0)
Методы решения:
1)  >
> 
a) Если a > 1, то исходное неравенство равносильно неравенству f(a) > g(a)
b) 0< a < 1 a в пределах от 0 до 1 сходное неравенство равносильно неравенству f(a) < g(a)
2)  >
> 
Не нашли, что искали? Воспользуйтесь поиском: