
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Алгебраические свойства векторного произведения. Для любых векторов , , и любого действительного числа :
Для любых векторов 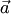 ,
, 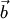 ,
, 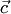 и любого действительного числа
и любого действительного числа 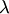 :
:
1.  ;
;
2. 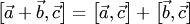 ;
;
3. 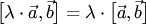 .
.
Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство "противоположно" закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.
Докажем первое свойство, предполагая, что векторы 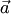 и
и 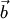 не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы
не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы 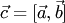 и
и 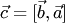 имеют равные длины
имеют равные длины  и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов
и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов 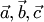 и
и 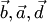 — правые, т.е. вектор
— правые, т.е. вектор 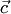 направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от 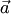 к
к 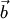 происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора
происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора 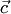 , а вектор
, а вектор 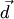 направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от 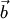 к
к 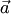 происходит в положительном направлении, если смотреть из конца вектора
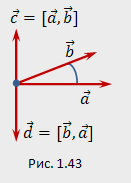
происходит в положительном направлении, если смотреть из конца вектора 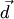 (рис. 1.43). Это означает, что векторы
(рис. 1.43). Это означает, что векторы 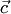 и
и 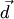 противоположно направлены. Следовательно,
противоположно направлены. Следовательно,  , что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).
, что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).
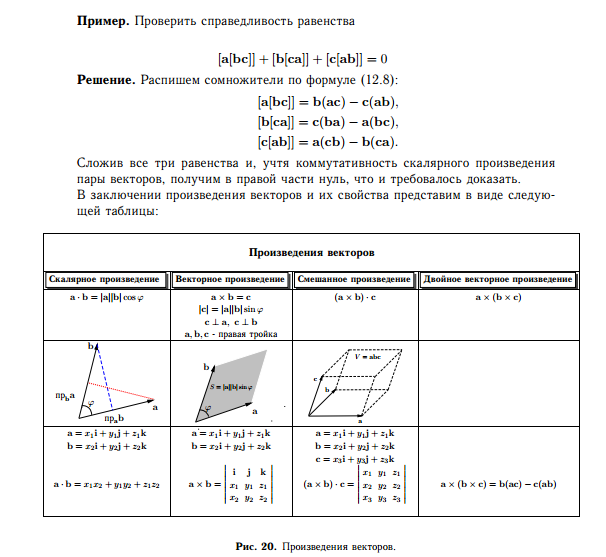
Координаты вектора с находим с помощью определителя матрицы:
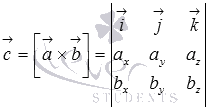
Рассчитываем определитель, приводим подобные, коэффициенты при I,J,k и будут координатами x, y, z соответственно.
Билет 12



Билет 13
Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём:
x + y = y + x − сложение коммутативно;
x + (y + z) = (x + y) + z − сложение ассоциативно;
x + 0 = x − существует единственный нулевой элемент 0 (x + 0 = x для любого x из L);
x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x (x + (−x) = 0 для любого x из L).
2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α· x, наываемый произведением α и x, причём:
α·(β · x) = (α·β) · x − умножнение на число ассоциативно:;
1 · x = x − для любого элемента x из L.
3. Операции сложения и умножения на число связаны соотношениями:
α·(x + y) = α· x + α· y − умножнение на число дистрибутивно относительно сложения элементов;
(α + β )· x = α· x + β · x − умножнение на вектор дистрибутивно относительно сложения чисел.
Набор векторов 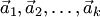 называется системой векторов.
называется системой векторов.
Система из 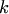 векторов
векторов 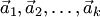 называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа 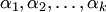 , не все равные нулю одновременно, что
, не все равные нулю одновременно, что
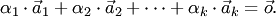
| (1.1) |
Система из 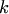 векторов
векторов 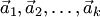 называется линейно независимой, если равенство (1.1) возможно только при
называется линейно независимой, если равенство (1.1) возможно только при  , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.
, т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.
Замечания 1.2
1. Один вектор  тоже образует систему: при
тоже образует систему: при 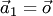 — линейно зависимую, а при
— линейно зависимую, а при 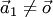 — линейно независимую.
— линейно независимую.
2. Любая часть системы векторов называется подсистемой.
Не нашли, что искали? Воспользуйтесь поиском: