Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.

4. Система из векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов 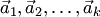линейно независима, а после присоединения к ней вектора 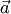оказывается линейно зависимой, то вектор 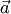можно разложить по векторам 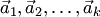, и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

Докажем, например, последнее свойство. Так как система векторов — линейно зависима, то существуют числа , не все равные 0, что. В этом равенстве . В самом деле, если , то . Значит, нетривиальная линейная комбинация векторов 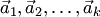равна нулевому вектору, что противоречит линейной независимости системы 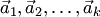. Следовательно, и тогда , т.е. вектор 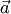есть линейная комбинация векторов 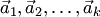. Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения и , причем не все коэффициенты разложений соответственно равны между собой (например, ).

Тогда из равенства получаем .

Следовательно, линейная комбинация векторов 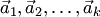равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов 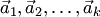. Полученное противоречие подтверждает единственность разложения.

Векторное пространство называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.

Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.

Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.

Совокупность n линейно независимых векторов n - мерного векторного пространства называется его базисом.

Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:

(x, y) = (y, x),

(α ·x, y) = α ·(x, y),

(x + y, z) = (x, z) + (y, z),

(x, x) > 0 при x ≠ 0, (0, 0) = 0,

то в пространстве L определено скалярное произведение (x, y).

Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.

Теорема 1 (неравенство Коши-Буняковского)

Для любых чисел .

Доказательство

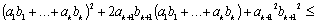При неравенство верно. Допустим, . Докажем, что . Перепишем это неравенство, частично раскрыв скобки: . Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство: А это и доказывает неравенство Коши-Буняковского.

Определение 2

1. Число 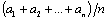называется средним арифметическим чисел . 2. Если , то число называется средним геометрическим чисел .

Теорема 3 (неравенство Коши)

Пусть , тогда . (1)

Доказательство

Шаг первый: сначала индукцией докажем это неравенство для натуральных чисел вида . При m=1 надо доказать, что . Это неравенство эквивалентно , то есть . Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть . (2) Докажем неравенство (1) для m=k+1, то есть докажем, что . В самом деле, . Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что 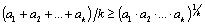, (3) и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим , тогда (3) будет иметь вид: После элементарных алгебраических преобразований получили: . Сократим неравенство на второй множитель правой части: . И, наконец, возведем обе части неравенства в степень : . Неравенство Коши доказано полностью.

Билет 14

Не нашли, что искали? Воспользуйтесь поиском: