Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.

Эллипсоид (рис. 4.18)

Каноническое уравнение:

- трехосный эллипсоид;

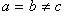- эллипсоид вращения вокруг оси Oz;

- эллипсоид вращения вокруг оси Oy;

- эллипсоид вращения вокруг оси Ox;

- сфера.

Сечения эллипсоида плоскостями - либо эллипс (окружность), либо точка, либо .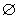

Конус второй степени (рис. 4.19)

Каноническое уравнение:

a = b - конус вращения (прямой круговой).

Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).

Эллиптический цилиндр (рис. 4.24)

Каноническое уравнение:

при a = b - круговой цилиндр.

Гиперболический цилиндр (рис. 4.25)

Каноническое уравнение:

Параболический цилиндр (рис. 4.26)

Каноническое уравнение:

Вопрос25 поверхности второго порядка (гиперболоиды, параболоиды) и их канонические уравнения.

Однополостный гиперболоид (рис. 4.20)

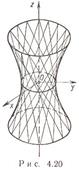
Каноническое уравнение:

a = b - однополостный гиперболоид вращения вокруг оси Oz.

Горловой эллипс: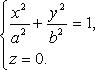

Асимптотический конус:

Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).

Двуполостный гиперболоид (рис. 4.21)

Каноническое уравнение:

a = b - двуполостный гиперболоид вращения вокруг оси Oz.

Асимптотический конус:

Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо .

Эллиптический параболоид (рис. 4.22)

Каноническое уравнение:

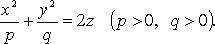
p = q - параболоид вращения вокруг оси Oz.

Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо .

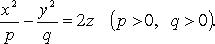
Гиперболический параболоид (рис. 4.23)

Каноническое уравнение:

Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).

Не нашли, что искали? Воспользуйтесь поиском: