
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решить систему матричным методом.


Составим матрицу системы.
 Составим матрицу свободных членов
Составим матрицу свободных членов 
Составим матрицу неизвестных 
Найдем обратную матрицу 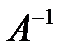
 ;
;  ;
;  ;
; 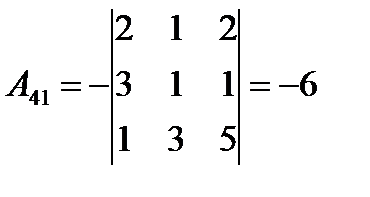
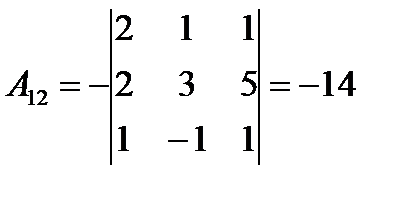 ;
;  ;
; 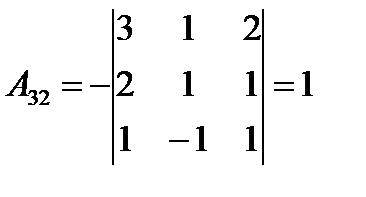

 ;
;  ;
;  ;
; 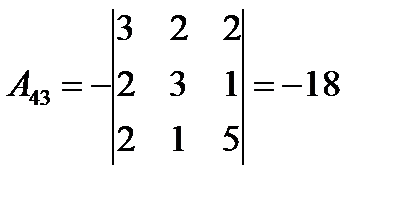
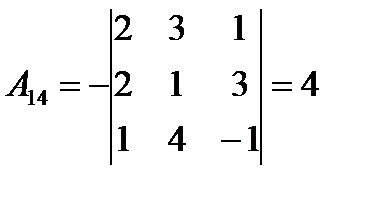 ;
;  ;
; 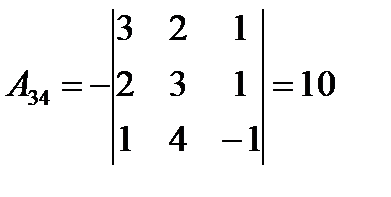 ;
; 




Решение.
Найти длину ребра А1А2




 и
и 
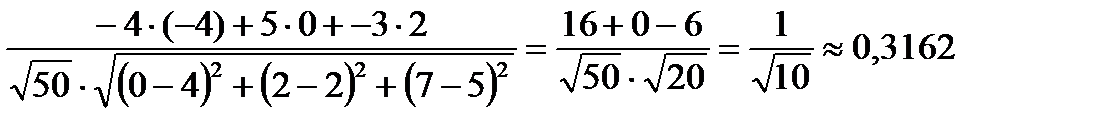
Следовательно,  ДОПИСАТЬ
ДОПИСАТЬ













6)



 После преобразований получим
После преобразований получим




 плоскости
плоскости  . И тогда уравнение высоты запишется в виде:
. И тогда уравнение высоты запишется в виде:



Задание №3

Решение. Пусть дан квадрат ABCD
Представим данное уравнение прямой в виде AB:  .
.
Тогда уравнение прямой, параллельной данной примет вид CD:  , где С необходимо найти.
, где С необходимо найти.
Теперь возьмём какую-нибудь точку на прямой AB. Например, R(2,1). Найдём точку Q, которая будет симметрична R относительно точки P(-1,0).
По определению центральной симметрии PQ = RP.
Отсюда P - середина отрезка QR. P(-1,0); Q(x,y); R(2,1)
-1 = (x + 2)/2,
0 = (y + 1)/2.
x + 2 = -2,
y + 1 = 0.
x = -4, y = -1.
Q(-4,-1)
Эта точка лежит на прямой  , то есть она удовлетворяет уравнению этой прямой.
, то есть она удовлетворяет уравнению этой прямой.

Получаем, что уравнение прямой CD: 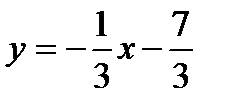 или
или 
Определим длину стороны квадрата, расстояние между параллельными прямыми АВ и CD (квадрат): получаем, что AB = BC = 12 (расстояние между прямыми AB и CD будет как раз 12, а это и есть сторона квадрата).
Прямые BC и AD перпендикулярны прямым AB и CD.
Используем утверждение о том, что перпендикулярные прямые имеют вид:
Ax + By + C = 0 и Bx - Ay + D = 0.
Уравнение прямой AB x+3y-5=0 => уравнение BC 3x-y+C=0;
AD 3x-y+D=0.
Получаем уравнения BC: 3x-y+C=0 и AD: 3x-y+C+12=0
(так как сторона квадрата равна 12).
Опять возьмём две симметричных точки относительно P.
На BC M(1,3+C), на AD N(x,y). P - середина MN
-1 = (1 + x)/2,
0 = (3 + C + y)/2.
x + 1 = -2,
3 + C + y = 0.
x = -3, y = -C - 3. N(-3,-C-3)
N лежит на прямой AD: 3x-y+C+12=0.
3*(-3) - (-C-3) + C + 12 = 0
-9 + C + 3 + C + 12 = 0
2*C = -6
C = -3
Ответ: AB x+3y-5=0
BC 3x-y-3=0
CD x+3y+7=0
AD 3x-y+9=0
Схематический чертеж.
| y | ||||||||||
| |||||||||||
| x | |||||||||||
| |||||||||||
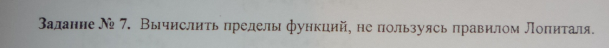


Решение.
а)

б)

в)



г)
 Вычислим предел показателя
Вычислим предел показателя


Таким образом


Решение.
а)

б)


в)

г)

д)

Продифференцируем обе части функции по х




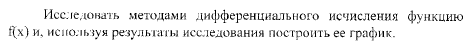

Решение.
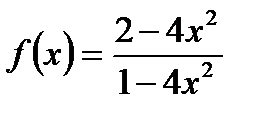
Воспользуемся общей схемой исследования функции.
1. Областью определения функции является множество  .
.
2. Точки разрыва: 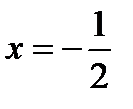 ,
,  . Определим род точки разрыва
. Определим род точки разрыва 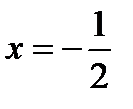 .
.


Точка 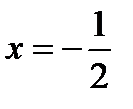 разрыва второго рода.
разрыва второго рода.
Следовательно, 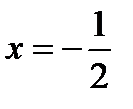 – является вертикальной асимптотой.
– является вертикальной асимптотой.
Определим род точки разрыва  .
.

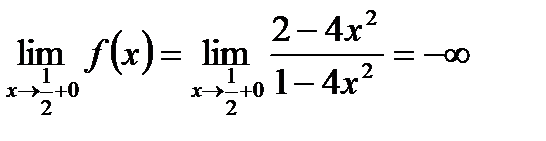
Точка 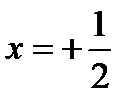 разрыва второго рода.
разрыва второго рода.
Следовательно, 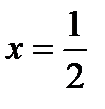 – является вертикальной асимптотой.
– является вертикальной асимптотой.
Определим точки пересечения с осями координат:
 А(0;2)
А(0;2)
 В
В  , С
, С 
3. Исследуем функцию на четность и нечетность.
Если  – функция четная
– функция четная
Если  – функция нечетная
– функция нечетная
 Функция является четной.
Функция является четной.

4. Исследуем функцию на монотонность и экстремумы.
| x |
| |
| + |
| -1/2 |
| 1/2 |
| |
| + |


Функция возрастает на интервале 
5. Определим интервалы выпуклости и точки перегиба

| x |
| |
| -1/2 |
| 1/2 |
| + |
| |

График функции выпуклый вверх на интервале 
График функции выпуклый вниз (вогнутый) на интервале 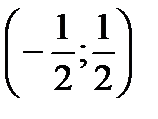
6. Найдем асимптоты графика функции.
y=kx+b




y=1 – горизонтальная асимптота.
7. Строим график.
| y | ||||||||||||||
| x | ||||||||||||||
Не нашли, что искали? Воспользуйтесь поиском: