
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Аксиомы стереометрии и их следствия
Периодичность
Функции  — периодические с периодом 2π, функции
— периодические с периодом 2π, функции  и
и  — c периодом π.
— c периодом π.
35.
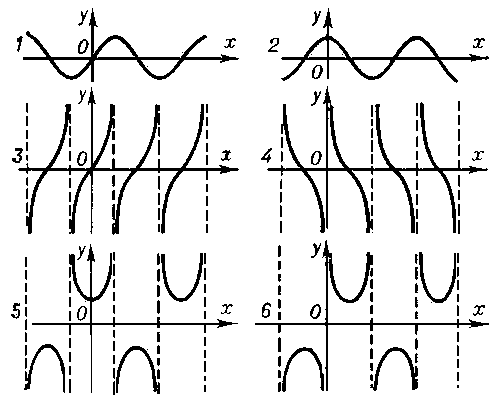
Рис. 2. Графики тригонометрических функций: 1 — синуса; 2 — косинуса; 3 — тангенса; 4 — котангенса; 5 — секанса; 6 — косеканса.
36. 

Арксинусом числа m называется такое значение угла x, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго возрастающей.
является строго возрастающей.
-
 при
при 
-
 при
при 
-
 (область определения),
(область определения), -
 (область значений).
(область значений).

Арккосинусом числа m называется такое значение угла x, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго убывающей.
является строго убывающей.
-
 при
при 
-
 при
при 
-
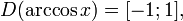 (область определения),
(область определения), -
 (область значений).
(область значений).

Арктангенсом числа m называется такое значение угла  , для которого
, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго возрастающей.
является строго возрастающей.
-
 при
при 
-
 при
при 
-

-
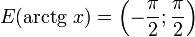

Арккотангенсом числа m называется такое значение угла x, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго убывающей.
является строго убывающей.
-
 при
при 
-
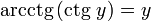 при
при 
-

-


37. Основной способ решения тригонометрических неравенств состоит в их сведении к неравенствам вида
| sin x Ú a, cos x Ú a, tg x Ú a, ctg x Ú a, |
где a Î R, символ "Ú" означает знак сравнения и заменяет любой из знаков ">", " ≥ ", "<", " ≤" и использовании следующих утверждений.
Утверждение 1. Множество решений неравенства
| sin x > a |
- R, если a < -1;
-
 (arcsin a + 2p k; p - arcsin a + 2p k), если -1 ≤ a < 1;
(arcsin a + 2p k; p - arcsin a + 2p k), если -1 ≤ a < 1; - Пустое множество, если a ≥ 1.

Утверждение 2. Множество решений неравенства
| sin x < a |
есть
- R, если a > 1;
-
 (-p - arcsin a + 2p k; arcsin a + 2p k), если -1 < a ≤ 1;
(-p - arcsin a + 2p k; arcsin a + 2p k), если -1 < a ≤ 1; - Пустое множество, если a ≤ -1.

Утверждение 3. Множество решений неравенства
| cos x > a |
есть
- R, если a < -1;
-
 (2p k - arccos a; 2p k + arccos a), если -1 ≤ a < 1;
(2p k - arccos a; 2p k + arccos a), если -1 ≤ a < 1; - Пустое множество, если a ≥ 1.

Утверждение 4. Множество решений неравенства
| cos x < a v |
есть
- R, если a > 1;
-
 (2p k + arccos a; 2p(k + 1) - arccos a), если -1 < a ≤ 1;
(2p k + arccos a; 2p(k + 1) - arccos a), если -1 < a ≤ 1; - Пустое множество, если a ≤ -1.

Утверждение 5. Множество решений неравенства
| tg x > a |
есть 

Утверждение 6. Множество решений неравенства
| tg x < a |
есть 

Утверждение 7. Множество решений неравенства
| ctg x > a |
есть  (p k; arcctg a + p k).
(p k; arcctg a + p k).

Утверждение 8. Множество решений неравенства
| ctg x < a |
есть  (arcctg a + p k; p(k + 1))
(arcctg a + p k; p(k + 1))

38. Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
| Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны. | 
|
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β, 
|

|
Аксиомы стереометрии и их следствия
Не нашли, что искали? Воспользуйтесь поиском: