Определение вектора. Основные операции с векторами и определения.

Определение вектор - упорядоченная пара точек пространства.

- Вектора называются коллинеарными а ║в, если прямые, которые через них проходят, параллельны.
- вектора называются прямоколлинеарными АВ ↑↑ CD, если точка А и С лежат по одну сторону от прямой, проходящей через B и D.
- вектора называются противоколлинеарными АВ ↑↓ CD, если точки А и С по разные стороны от прямой, проходящей через B и D.
Длина вектора - длина отрезка, определяющего вектор. Обозначается длина ׀а׀, │АВ│. Вектор а называется единичным, если ׀а׀ =1.
Два вектора называются равными, если они прямоколлинеарны и имеют одинаковую длину.
Векторы называются компланарны, если они параллельны одной плоскости.
Геометрический вектор - направленный отрезок. | AB |=| a | - длинна.
2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых.
Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях.
2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длину.

AB = CDPQ ≠ PREF ≠ GH
Действия над векторами
1) умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми:
а) А || В.
б) l>0, то А ­­ В, l<0, то А ­¯ В.
в)l>1, то А < В,)l<1, то А > В
2) Разделить вектор на число n значит умножить его на число, обратное n: а /n= a *(1/n).
3) Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора.
4) Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.

Операции с векторами.
Сложение векторов:
Свойства операции сложения:
1 ) коммутативность а + b = b + a;

2 ) ассоциативность (a + b) + c = a + (b + c);
Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить.
a + b + c = a + (b + c)
a + b + c = (a + b)+ c

Разность a − b

векторов а и b = вектору c который в сумме с вектором b
дает вектор а
3) а + 0 = а;
4) для любого вектора а существует противоположный вектор (-а), что а +(-а) = 0.
Умножение вектора на число
Произведение вектора a(a1; a2) на число λ называется вектор (λa1; λa2), т.е. (a1; a2) λ = (λa1; λa2).
Для любого вектора a и чисел λ, μ

Для любого вектора a и b и числа λ

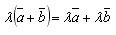
Свойства умножения на число:
5 ) 1*а = а;
6) ассоциативность по умножению чисел
λ (µа) = (λµ) а, λ, µ є Ɍ;
7) дистрибутивность по сложению чисел
(λ + µ) a = λa + µa, λ, µ є Ɍ;
8) дистрибутивность по сложению векторов
λ(a + b) = λa + λb, λ є Ɍ;
9) для любых векторов а и b существует такой вектор х, что а + х = b (называется разностью векторов а и b);
10 ) (-1) x a = - a.

Не нашли, что искали? Воспользуйтесь поиском: