Базис.Разложение по базису

Определение. Базисом в пространстве Rⁿ называется любая система из n -линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.
Пусть 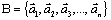– базис пространства Rⁿ и . Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что .
Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
Пример. Доказать, что векторы образуют базис в R³.
Решение. Покажем, что равенство 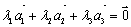возможно только при λ₁ = λ₂ = λ₃ =0:

или
Решив систему, получим λ₁=0, λ₂=0, λ₃=0. Так как все λ _i =0 (i =1,2,3), то 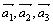- линейно независимы. Они могут составить базис в R³.
Очевидно, любой новый набор из векторов может тоже быть взятым в качестве базиса в R³. Итак, базис может быть выбран неединственным образом.
Пример. Разложить вектор по базису .
Решение. 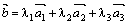. Подставим координаты всех векторов и выполним действия над ними:

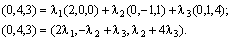
Приравняв координаты, получим систему уравнений:

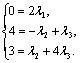
Решим ее: .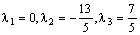
Таким образом, получим разложение: .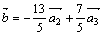
В базисе вектор имеет координаты .
Замечание. В каждом n -мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе.

Не нашли, что искали? Воспользуйтесь поиском: