Площадь многоугольника

Формулы для вычисления площади прямоугольника, треугольника, параллелограмма были выведены давно. В геометрии их обосновывают, исходя из определения площади, при этом численное значение площади называют площадью, а численное значение длины отрезка-длиной.

Теорема. Площадь прямоугольника равна произведению длин соседних его сторон.

Напомним, что слово «площадь» в этой формулировке означает численное значение площади, а слово «длина» - численное значение длины отрезка.

Доказательство. Если F- данный прямоугольник, а числа а, b -длины его сторон, то S(F) = а×b. Докажем это.

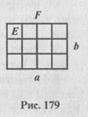Пусть а и b - натуральные числа. Тогда прямоугольник F можно разбить на единичные квадраты. (рис. 179): F= Е Å Е Å Е Å ... Å Е. Всего их а×b, так как имеем b рядов, в каждом из которых а квадратов. Отсюда S(F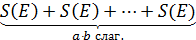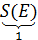) = )=a×b× =a×b.

Пусть теперь а и b - положительные рациональные числа: а = , где т, п,р,q - натуральные числа.

Приведем данные дроби к общему знаменателю: a = 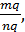b = 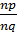. Разобьем сторону единичного квадрата Е на пq равных частей. Если через точки деления провести прямые, параллельные сторонам, то квадрат Е разделится на (пq)² более мелких квадратов. Обозначим площадь каждого такого квадрата Е _1. Тогда S(Е) = (пq)²×S(Е₁), а поскольку S(Е) = 1, то S(Е₁) = .

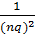Так как а = 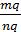, b = 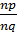, то отрезок длиной 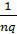укладывается на стороне а точно тq раз, а на стороне b - точно пр раз. Поэтому данный прямоугольник F будет состоять из тq×пр квадратов Е₁. Следовательно,

S(F) = mq×np×S(E₁)=mq×np× 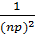= 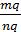× 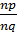= × = a×b.

Таким образом доказано, что если длины сторон прямоугольника выражены положительными рациональными числами а и b, то площадь этого прямоугольника вычисляется по формуле S (F) = а×b.

Случай, когда длины сторон прямоугольника выражаются положительными действительными числами, мы опускаем.

Из этой теоремы вытекает следствие: площадь прямоугольного треугольника равна половине произведения его катетов.

Теорема. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

Доказательство. Пусть АВСD - параллелограмм, не являющийся прямоугольником (рис. 180). Опустим перпендикуляр СЕ из вершины С на прямую АD. Тогда S(АВСD) = S(АВСD) + S(СDЕ).

Опустим перпендикуляр ВF из вершины В на прямую АD. Тогда S(АВСЕ) = S(ВСЕF) + S(АВF).

Так как треугольники АВF и СDЕ равны, то равны и их площади. Отсюда следует, что S(АВСD) = S(ВСЕF), т.е 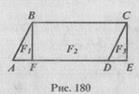. площадь параллелограмма АВСD равна площади прямоугольника ВСЕF и равна ВС×ВF, а так как ВС = АD, то S(АВСD) = АD×ВР.

Из этой теоремы вытекает следствие: площадь треугольника равна половине произведения его стороны на проведенную к ней высот

Заметим, что слова «сторона» и «высота» в данных утверждениях обозначают численные значения длин соответствующих отрезков.

Теорема. Площадь правильного многоугольника равна половине произведения его периметра на радиус вписанной окружности.

Если периметр правильного многоугольника обозначить буквой Р, радиус вписанной окружности - r, а площадь правильного многоугольника - S, то, согласно данной теореме, S = Р×r.

Доказательство. Разобьем правильный n -угольник на п треугольников, соединяя отрезками вершины n -угольника с центром вписанной окружности (рис. 181). Эти треугольники равны. Площадь каждого из них равна а_n × r, где а_n - сторона правильного n -угольника. Тогда площадь многоугольника равна а_n × r×п, но а_n×п = Р. Следовательно, S = Р×r.

Если F - произвольный многоугольник, то его площадь находят, разбивая многоугольник на треугольники (или другие фигуры, для которых известны правила вычисления площади). В связи с этим возникает вопрос: если один и тот же многоугольник по-разному разбить на части и найти их площади, то будут ли полученные суммы площадей частей многоугольника одинаковыми? Доказано, что условиями, сформулированными в определении площади, площадь всякого многоугольника определена однозначно.

Кроме равенства и равновеликости фигур в геометрии рассматривают отношение равносоставленности. С ним связаны важные свойства фигур.

Многоугольники F₁ и F₂ называются равносоставленными, если их можно разбить на соответственно равные части.

Например, равносоставлены параллелограмм АВСD и прямоугольник FВСЕ (рис. 180), так как параллелограмм состоит из фигур F₁ и Р₂, а прямоугольник - из фигур F₂ и F₃, причем F₁ = F₃.

Нетрудно убедиться в том, что равносоставленные фигуры равновелики.

Венгерским математиком Ф.Бойяи и немецким любителем математики П.Гервином была доказана теорема: любые два равновеликих многоугольника равносоставлены. Другими словами, если два многоугольника имеют равные площади, то их всегда можно представить состоящими из попарно равных частей.

Теорема Бойяи-Гервина служит теоретической базой для решения задач на перекраивание фигур: одну разрезать на части и сложить из нее другую. Оказывается, что если данные фигуры многоугольные и имеют одинаковые площади, то задача непременно разрешима.

Доказательство теоремы Бойяи-Гервина достаточно сложное. Мы докажем только утверждение о том, что всякий треугольник равносоставлен с некоторым прямоугольником, т.е. всякий треугольник можно перекроить в равновеликий ему прямоугольник.

Пусть дан треугольник АВС (рис. 182). Проведем в нем высоту ВD и среднюю линию КL. Построим прямоугольник, одной стороной которого является АС, а другая лежит на прямой КL. Так как пары треугольников АРК и КВТ, а также CLM и ТВL равны, то треугольник АВС и прямоугольник АРМС равносоставлены.

Упражнения

1. Воспроизведите доказательство теорем о площади прямоугольника и параллелограмма и покажите, какие свойства площади были при этом использованы.

2. Докажите, что площадь любого треугольника равна половине произведения его стороны на проведенную к ней высоту.

3. Площадь прямоугольника равна 12 см, длины его сторон выражаются натуральными числами. Сколько различных прямоугольников можно построить согласно этим условиям?

4. Прямые а и b параллельны. Точка В движется по прямой b, занимая положение В₁, В₂, В₃ и т.д., а точки А и С остаются неподвижными. Равновелики ли треугольники АВ,С, АВ₂С и т.д.?

5. Длины сторон параллелограмма 6 и 12 см, а высота его, проведенная к меньшей стороне, 10 см. Найдите высоту, проведенную к большей стороне параллелограмма.

6. Докажите, что всякая трапеция равносоставлена с прямоугольником, одна сторона которого равна средней линии трапеции, а другая ее высоте.

Не нашли, что искали? Воспользуйтесь поиском: