
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ДЕ 2. Дискретные случайные величины
1. А – случайное событие, U – дост. событие. Тогда вероятность P(A+U) равно: 1
2. В одной урне 5 белых и 3 чёрных шара, в другой – 3 белых и 5 черных шаров, из каждой урны извлекли по 1 шару. Вероятность того, что хотя бы один из них черный, равно: 
3. В одной урне 6 белых и 4 черных шаров, в другой 5 белых и 5 черных шаров. Событие А – извлечение белого шара из первой урны, событие В – извлечение белого шара из второй урны, Тогда А и В: независимые события.
4. В первой партии деталей 15% нестандартных, во второй партии 25%, вероятность того, что деталь, наудачу взятая из наудачу выбранной партии не является стандартной, равна: 0,20
5. В первой партии деталей 40% нестандартных, во второй партии 10%. Вероятность того, что деталь, наудачу взятая из наудачу выбранной партии, не является стандартной, равна: 0,25
6. В первой урне 2 белых и 8 черных шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули 1 шар. Тогда вероятность того, что этот шар окажется белым, равна: 0,25
7. В урне 10 белых и 5 черных шаров. Тогда вероятность P(A) события А – извлечения красного шара равна: 0
8. Вероятность достоверного события равна: 1
9. Вероятность любого события, принадлежащего промежутку: [0;1]
10. Вероятность невозможного события равна: 0
11. Вероятность попадания при каждом выстреле равна 0,2. Вероятность ровно 2 попаданий при 14 выстрелах равно: 0,25
12. Вероятность попадания при каждом выстреле равна 0,6. Вероятность ровно 3 попаданий при 4 выстрелах равно: 0,25
13. Вероятность события есть: число
14. Вероятность того, что при двух подбрасываниях монеты орел выпадет только один раз, равна: 0,5
15. Вероятность того, что при подбрасывании двух игральных кубиков произведение выпавших очков окажется равным 6, равно: 
16. Вероятность того, что при четырех подбрасываниях монеты герб выпадет ровно 3 раза равна: 0,25
17. Гипотезами называются: попарно несовместные события, образующие полную группу событий.
18. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,4 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна: 0,94
19. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,7 соответственно. Тогда вероятность того, что цель будет поражена, равна: 0,94
20. Для произвольных событий А и В имеет место равенство: P(A+B) = p(A) + p(B) – p(AB)
21. Из урны, содержащей 4 белых и 6 черных шаров, извлекают одновременно два шара. Тогда вероятность того, что оба шара будут черными, равна: 
22. На конвейер поступают детали из двух цехов (поровну). Вероятность выпускать брак для этих цехов равны 0,01 и 0,02. Взятая с конвейера деталь оказалась браком. Вероятность того, что эта деталь из второго цеха, равна: 
23. Событие, которое не может наступить в результате рассматриваемого опыта, называется: невозможным
24. Сумма вероятностей гипотез в формуле полной вероятности равна: 1
25. Сумма двух событий наступает тогда и только тогда, когда: наступает хотя бы одно из событий
26. Находится по формуле: Бейеса
27. Формула Бейеса используется для вычисления вероятности: Р( 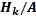 )
)
28. Формула полной вероятности: P(A)= 
29. Вероятность попадания при каждом выстреле равна 0,7. Тогда наивероятнейшее число попаданий при 6 выстрелах равно: 4
30. Для любых гипотез  и любого события А, имеющего положительную вероятность, справедливо равенство (k=1,…, n):
и любого события А, имеющего положительную вероятность, справедливо равенство (k=1,…, n): 
ДЕ 3 Дискретные и случайные величины (ДСВ)
№ 1 Дисперсия любой случайной величины: Не отрицательна.
№ 2 Закон распределения ДСВ- это таблица в которой представлены вероятности значений: принимаемые этой величиной.
№ 3 Закон распределения ДСВ- это таблица в которой представлены числовые значения: принимаемые этой величиной.
№ 4 Закон распределения случайной величины Х может быть представлена в таблице:
| Х | |||
| Р | 0,3 | 0,5 | 0,2 |
№ 5 значения принимаемые ДСВ: образуют конечное или счетное множество.
№ 6 Математическое ожидание каждой случайной величины: является действительным числом.
№ 7 монета подбрасываемая 2 раза закон распределения случайной величины Х, значение которой = числу выпавших решек, имеет вид:
| Х | |||
| Р | 
| 
| 
|
| Х | |||
| Р | а | b | с |
№ 8 Среди приведенных ниже распределений к ДСВ относятся: биномиальное.
№ 9 Среднее квадратичное отклонение любой случайной величины: не отрицательна.
№ 10 функция распределения произвольной случайной величины на всей вещественной оси: не убывает.
№ 12 функция распределения произвольной случайной величины на всей вещественной оси является: монотонной.
№ 13 ДСВ для закона таблицы:
| Х | |||
| Р | 0,1 | 0,5 | 0,4 |
№ 14: 0*0,1+1*0,5+2*0,4= 1,3
| Х | |||
| Р | 0,7 | 0,2 | 0,1 |
№ 15 Мат/ожид. ДСВ заданной табл. равно: 0,4
| Х | |||
| Р | m | 0,5 | 0,4 |
№ 16 = № 15
№ ДСВ заданно таблицей m равно: 0,1
№18=№15
№19=№17
№20=№15
№21=№17
№22=№17
№23: Fᶓ(х) 
| Х | |||
| ᶓ | 
| 
| 
|
№ 24 Ряд распределения случайной величины ᶓ значение которой = числу выпавших гербов, при подбрасывании монеты 2 раза имеет вид:
№ 25 Дисперсия мат/ожидания: D(X)= М(X2)- (M(X))2
№26 Дисперсия D(X) и мат/ожид M(X) случайной величины х связаны равенством: D(X)= М(X2)- (M(X))2
№ 27 Среднее квадратичное отклонение и дисперсия равны: δ(Х)= 
ДЕ 4. Непрерывные и случайные величины (НСВ).
№ 1 Дисперсия любой случайной величины: не отрицательна.
№ 2 Дисперсия постоянной величины равна: 0.
№ 3 Значения принимаемые любой НСВ: заполняет некоторый промежуток.
№ 4 Значения принимаемые любой НСВ: заполняет некоторый интервал.
№ 5 Мат/ожид каждой случайной величины: может быть любым действительным числом.
№ 6 Мат/ожид постоянной величины равно: самой постоянной.
№ 7 НСВ может иметь: равномерное распределение.
№ 8 НСВ может иметь: нормальное распределение.
№ 9 НСВ может иметь: экспоненциальное распределение.
№ 10 Для плотности распределения НСВ f(x) верно равенство: 
№ 11 Мат/ожид случайной величины с плотностью распределения f(x)={5е-5х} x>0 равно: 
№ 12 Кривая нормального распределения (график функции f(x)=  -
-  ): Гаусса.
): Гаусса.
№ 13 Дисперсия случайной величины распределенная по экспоненциальному закону с плотностью f(x)=  равна:
равна: 
№ 14 Мат/ожид случайной величины распределенная по экспоненциальному закону с плотностью f(x)=  равна:
равна: 
№ 15 Среднее квадратичное отклонение случайной величины распределенная по экспоненциальному закону с плотностью f(x)=  равна:
равна: 
№ 16 Функция плотности распределения нормального закона f(x)=  -
-  имеет max в точке: (m;
имеет max в точке: (m;  ).
).
№ 17 Среднее квадратичное отклонение случайной величины распределенная по равномерному закону f(x)= 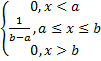 равно:
равно: 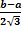
№ 18 НСВ ф-ция плотности которой задается выражением f(x)=  называется случайной величиной имеющей: показательное или экспоненциальное распределение.
называется случайной величиной имеющей: показательное или экспоненциальное распределение.
№ 19 Мат/ожид случайной величины распределенная по равномерному закону с плотностью f(x)= 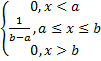 равно:
равно: 
№ 20 Дисперсия нормальной распределенной случайной величины с плотностью f(x)=  -
-  равно: δ2.
равно: δ2.
№ 21 Мат/ожид случайной величины с ф-цией распределения F(x)= 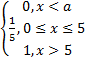 равно: 2,5
равно: 2,5
№ 22 Мат/ожид случайной величины с ф-цией распределения F(x)= 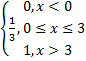 равно: 1,5
равно: 1,5
№ 23 Плотность распределения случайной величины f(x) b ее ф-ция распределения F(x) связанны формулами: f(x)=F´(x)
№ 24 Плотность вероятностей f(x)=  -
-  задается непрерывная случайная величина распределенная по: нормальному закону.
задается непрерывная случайная величина распределенная по: нормальному закону.
№ 25 Параметр m в формуле плотности распределения вероятность нормального закона f(x)=  -
-  : Мат/ожидание.
: Мат/ожидание.
№ 26 Параметр δ в формуле плотности распределения вероятность нормального закона f(x)=  -
-  : Среднее квадратичное отклонение.
: Среднее квадратичное отклонение.
№ 27 Плотность распределения НСВ f(x) имеет вид: f(x)=  тогда вероятность P(-0.1<X<0.1) равна: -0.0001
тогда вероятность P(-0.1<X<0.1) равна: -0.0001
№ 28 Случайная величина задаваемая плотностью вероятности P(x)= 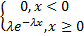 распределена по закону: экспоненциальному.
распределена по закону: экспоненциальному.
№ 29 Плотность вероятности Р(x)=  -
-  задается случайная величина по: нормальному закону(Гаусса).
задается случайная величина по: нормальному закону(Гаусса).
ДЕ 5.Статистика.
1. Выборка составляется таким образом, что случайно отбираемые из генеральной совокупности объекты возвращаются в эту совокупность и могут быть отобраны ещё: повторной
2. Выборка ….. объекты не возвращаются: бесповторные
3. Выборочное среднее выборки 0,25; 0,35; 0,45: 0,35
4. Выборочная дисперсия выборки 0,25; 0,35; 0,45 равна: 
5. Выборочное среднее выборки 3;5;6;14: 7
6. Выборочная дисперсия выборки 3;5;6;14: 17,5
7. Выборочное среднее выборки 5;3;0;1;4;2;5;4;1;5: 3
8. Выборочная дисперсия выборки 5;3;0;1;4;2;5;4;1;5: 3,2
9. Выборочное среднее постоянной равно: постоянной
10. Выборочное среднее: аналог математического ожидания
11. Гистограмма обычно строится для: непрерывно распределенного признака
12. Гистограмма является оценкой: плотности распределения
13. Гистограмма – это: ступенчатая фигура, состоящая из прямоугольников
14. Множество всех однотипных объектов, для которых проводится статистический анализ, называется: генеральной совокупностью
15. Множество отбираемых из генеральной совокупности объектов, называется: выборкой
16. Объемом выборки называется: число составляющих её значений
17. Относительная частота вариантов 5 в вариационном ряде 00012234444577: 
18. Относительная частота варианта 7: 
19. Полигон обычно строится для: дискретного статистического ряда
20. Полигон частот выборки: 5;3;0;1;4;2;5;4;1;5 – это ломанная линия, соединяющая точки и многоточия: (0;1),(1;2),(2;1)...
21. Полигон: ломаная линия
22. Ранжирование опытных данных называется: расположение опытных данных в порядке не убывания
23. Сумма S прямоугольников, составляющих гистограмму относительных частот: 1
24. Сумма S прямоугольников, составляющих гистограмму частот: объему выборки
25. Сумма частот всех вариантов равно: объему выборки
26. Частота вариантов 5 в вариационном ряде с номера 17 равно: 1
27. Эффективной называется оценка, которая при заданном объеме выборки имеет: минимальную дисперсию
28.  – выборка объема n.
– выборка объема n. 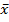 – выборочное среднее:
– выборочное среднее: 
29.  – выборка объема n. Выборочная дисперсия.
– выборка объема n. Выборочная дисперсия.  вычисляется по формуле:
вычисляется по формуле: 

30. Оценка  параметра ϴ является несмещенной, если её математическое ожидание М(
параметра ϴ является несмещенной, если её математическое ожидание М( ) равно: М(
) равно: М(  )= ϴ
)= ϴ
Не нашли, что искали? Воспользуйтесь поиском: