
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Набір завдань з геометрії, І рівень
1. При якому додатному значенні п модуль вектора  дорівнює 6?
дорівнює 6?
А) 8; Б) 2; В)  ; Г)
; Г) 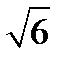 .
.
2. Величини двох кутів паралелограма відносяться як 8:7. Знайдіть більший кут паралелограма.
А) 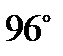 ; Б)
; Б) 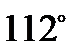 ; В)
; В)  ; Г)
; Г)  .
.
3. Знайдіть модуль вектора 
А) 8; Б) 30; В)  ; Г)
; Г)  .
.
4. Площини квадратів АВСD і ABKL перпендикулярні, АВ = 2 см. Знайти відстань між точками K і D.
А)  см; Б)
см; Б)  см; В) 4 см; Г)
см; В) 4 см; Г) 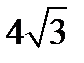 см.
см.
5. Сума довжин трьох сторін квадрата дорівнює 18 см. Знайти периметр квадрата.
А) 6 см; Б) 12 см; В) 18 см; Г) 24 см.
6. Сторона ромба дорівнює 13 см, а одна з його діагоналей – 24 см. Знайдіть довжину другої діагоналі ромба.
А)  см; Б)
см; Б)  см; В) 10 см; Г) 5 см.
см; В) 10 см; Г) 5 см.
7. Двогранний кут дорівнює  . На одній із його граней дано точку, розташовану на відстані 6 см від другої грані. Знайдіть відстань від цієї точки до ребра двогранного кута.
. На одній із його граней дано точку, розташовану на відстані 6 см від другої грані. Знайдіть відстань від цієї точки до ребра двогранного кута.
А) 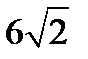 см; Б)
см; Б)  см; В) 6 см; Г) 3 см.
см; В) 6 см; Г) 3 см.
8. Точка, яка лежить на одній із граней двогранного кута, розташована на відстані 14 см від ребра і на відстані 7 см від другої грані. Знайдіть величину двогранного кута.
А)  Б)
Б)  ; В)
; В)  ; Г)
; Г)  .
.
9. Трикутник АВС подібний трикутнику KML,  . Знайти градусну міру кута С.
. Знайти градусну міру кута С.
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г) 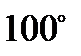 .
.
10. Сторони паралелограма дорівнюють 4 см і 7 см, а кут між ними  . Знайти довжину більшої діагоналі паралелограма.
. Знайти довжину більшої діагоналі паралелограма.
А)  см; Б)
см; Б)  см; В)
см; В) 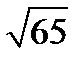 см; Г)
см; Г)  см.
см.
11. Діагональ прямокутника дорівнює 16 см і утворює з його стороною кут  . Знайдіть більшу сторону прямокутника.
. Знайдіть більшу сторону прямокутника.
А) 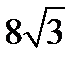 см; Б)
см; Б) 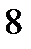 см; В)
см; В)  см; Г)
см; Г)  см.
см.
12. Обчисліть площу трикутника, дві сторони якого дорівнюють 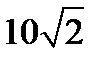 см і 9 см, а кут між ними −
см і 9 см, а кут між ними −  .
.
А) 45 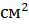 ; Б)
; Б) 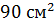 ; В)
; В) 
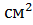 ; Г)
; Г) 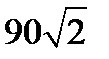
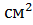 .
.
13. Коло задано рівнянням  . Яка з точок належить колу?
. Яка з точок належить колу?
А) (–3;3); Б) (–3;4); В) (5;1); Г) (0;6).
14. Прямокутник зі сторонами 5 см і 6 см обертається навколо більшої сторони. Знайдіть довжину діаметра утвореного циліндра.
А) 5 см; Б) 10 см; В) 6 см; Г) 12см.
15. Бічна сторона рівнобедреного трикутника дорівнює 15 см, а висота, проведена до основи, – 9 см. Знайдіть довжину основи рівнобедреного трикутника.
А) 6 см; Б) 12 см; В) 18см; Г) 24 см.
16. Сторона квадрата дорівнює 4 см. Знайдіть його діагональ.
А) 6 см; Б)  см; В)
см; В)  см; Г) 8 см.
см; Г) 8 см.
17. Яка з фігур є правильним многокутником?
А) трапеція; Б) квадрат;
В) прямокутний трикутник; Г) коло.
18. У прямокутній трапеції тупий кут утричі більший за гострий. Знайдіть градусну міру гострого кута трапеції.
А)  Б)
Б) 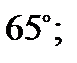 В)
В)  Г)
Г) 
19. Чотири точки А, В, С, D не лежать в одній площині. По якій прямій перетинаються площини А В С і А В D?
А) АВ; Б) ВС; В) СD; Г) АD.
20. Чотири точки А, В, С, D не лежать в одній площині. По якій прямій перетинаються площини А В D і В C D?
А) ВC; Б) ВD; В) AB; Г) АD.
21. Дано точку А, яка не належить прямій а. Скільки площин, паралельних а, можна провести через А?
А) Тільки дві; Б) Жодної;
В) Нескінчену множину; Г) Тільки одну.
22. Дано точку А, яка не належить площині  . Скільки площин, паралельних
. Скільки площин, паралельних  , можна провести через А?
, можна провести через А?
А) Тільки три; Б) Нескінчену множину;
В) Жодної; Г) Тільки одну.
23. Яка з наведених точок належить осі Оz прямокутної системи координат у просторі?
А)  Б)
Б)  В)
В)  Г)
Г) 
24. Яка з наведених точок лежить у площині Oxz прямокутної системи координат у просторі?
А)  Б)
Б)  В)
В)  Г)
Г) 
25. Виберіть правильне закінчення фрази: «Через точку, що не належить даній площині …»:
А) можна провести нескінченну множину площин, паралельних даній площині; Б) можна провести тільки одну площину, паралельну даній площині;
В) можна провести тільки дві площини, паралельні даній площині; Г) не можна провести жодної площини, паралельної даній площині.
26. Виберіть правильне закінчення фрази: «Через точку, що не лежить на даній прямій…»:
А) можна провести тільки одну площину, паралельну даній прямій; Б) можна провести нескінченну множину площин, паралельних даній прямій;
В) неможна провести жодної площини, паралельної даній прямій; Г) можна провести тільки дві площини, паралельні даній прямій.
27. У просторі дано пряму а і точку А поза нею. Скільки існує прямих, що є перпендикулярними до прямої а і проходять через точку А?
А) Жодної; Б) Нескінченна множина;
В) Одна; Г) Визначити неможливо.
28. З точки до площини проведено похилу, проекція якої на площину дорівнює 15 см, а відстань від цієї точки до площини становить 8 см. Знайдіть довжину похилої.
А) 17 см; Б) 23 см; В) 7 см; Г) 24 см.
29. З точки до площини проведено похилу завдовжки 10 см; відстань від цієї точки до площини дорівнює 8 см. Знайдіть проекцію похилої на площину.
А) 18 см; Б) 2 см; В) 6 см; Г) 25 см.
30. Дано куб  зі стороною 5 см. Знайдіть відстань між
зі стороною 5 см. Знайдіть відстань між  і
і 
А) 10 см; Б) 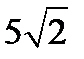 см; В) 5 см; Г) 25 см.
см; В) 5 см; Г) 25 см.
31. Дано куб  зі стороною 6 см. Знайдіть відстань між
зі стороною 6 см. Знайдіть відстань між  і
і  .
.
А) 12 см; Б) 3 см; В) 6 см; Г)  см.
см.
32. Похила завдовжки 12 м утворює з площиною кут  . Знайдіть довжину проекції цієї похилої на площину.
. Знайдіть довжину проекції цієї похилої на площину.
А) 6 м; Б) 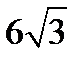 м; В) 24 м; Г)
м; В) 24 м; Г)  м.
м.
33. Похила АВ завдовжки  см утворює з площиною кут
см утворює з площиною кут  . Знайдіть відстань від кінця похилої до площини.
. Знайдіть відстань від кінця похилої до площини.
А) 8 см; Б) 6 см; В) 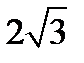 см; Г)
см; Г)  см.
см.
34. Дано куб  з ребром 8 см. Знайдіть відстань між прямими
з ребром 8 см. Знайдіть відстань між прямими  і
і 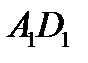 .
.
А) 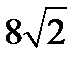 см; Б) 8 см; В) 6 см; Г) 10 см.
см; Б) 8 см; В) 6 см; Г) 10 см.
35. Дано куб  з ребром 5см. Знайдіть відстань між прямими
з ребром 5см. Знайдіть відстань між прямими  і
і 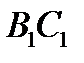 .
.
А) 10 см; Б) 5 см; В) 15 см; Г) 8см.
36. Яка з наведених точок належить осі Оz прямокутної системи координат у просторі?
А) 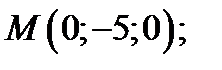 Б)
Б) 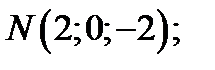 В)
В)  Г)
Г) 
37. Яка з наведених точок лежить у площині Oxz прямокутної системи координат у просторі?
А)  Б)
Б) 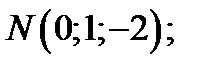 В)
В)  Г)
Г) 
38. Знайдіть модуль вектора 3  , якщо
, якщо  .
.
А) 6; Б) 9; В) 12; Г) 18.
39. Знайдіть основу рівнобедреного трикутника, периметр якого дорівнює 28 см, а основа на 8 см менша від бічної сторони.
А) 20 см; Б) 12см; В) 8 см; Г) 4см.
ІІ рівень
1. Один із катетів прямокутного трикутника дорівнює 30 см, а радіус описаного навколо нього кола – 17 см. Обчисліть площу даного трикутника.
2. Висота рівнобедреного трикутника, проведена до бічної сторони, ділить її на відрізки завдовжки 4 см і 16 см, рахуючи від вершини кута при основі. Знайдіть основу трикутника.
3. Висоти паралелограма дорівнюють 8 см і 12 см, а кут між ними  . Знайдіть площу паралелограма.
. Знайдіть площу паралелограма.
4. У рівнобічній трапеції ABCD основа ВС дорівнює 6 см, висота трапеції дорівнює  см, а бічна сторона утворює з основою AD кут
см, а бічна сторона утворює з основою AD кут  . Знайдіть основу AD трапеції.
. Знайдіть основу AD трапеції.
5. Розв’язати рівняння 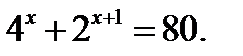
6. Розв’язати рівняння 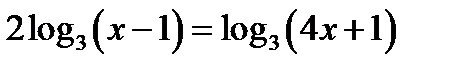 .
.
7. Знайти невизначений інтеграл 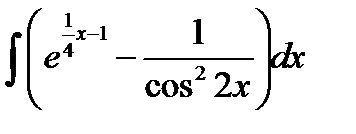 .
.
8. Відомо, що  Виразити
Виразити  через а і b.
через а і b.
9. Знайти площу фігури, обмеженої лініями  і
і  .
.
10. Знайти 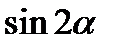 , якщо
, якщо  .
.
11. Знайти проміжки спадання функції 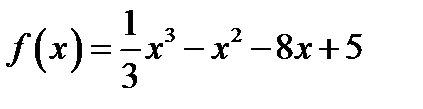 .
.
12. Розв’язати рівняння 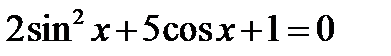 .
.
13. Розв’язати нерівність  .
.
14. Розв’язати рівняння 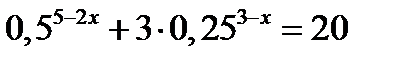 .
.
15. Знайдіть область визначення функції  .
.
16. Розв’яжіть рівняння 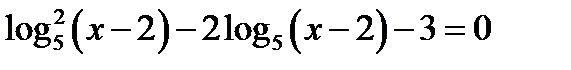 .
.
17. Знайдіть визначений інтеграл  .
.
18. Знайдіть х, якщо  .
.
19. Точка М знаходиться поза площиною прямокутного трикутника АВС, у якого  90
90  ; АС = 8 см; ВС = 6 см. Точка М знаходиться на однакових відстанях від вершин трикутника. Знайдіть цю відстань, якщо відстань від точки М до площини трикутника дорівнює 12 см.
; АС = 8 см; ВС = 6 см. Точка М знаходиться на однакових відстанях від вершин трикутника. Знайдіть цю відстань, якщо відстань від точки М до площини трикутника дорівнює 12 см.
20. Розв’яжіть нерівність 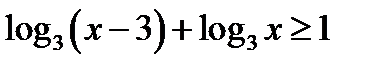 .
.
21. Знайдіть точки мінімуму функції 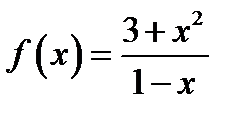 .
.
22. Розв’яжіть рівняння 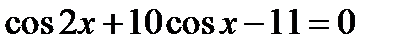 .
.
23. Розв’яжіть нерівність  .
.
24. Дано  і
і 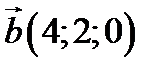 . Знайдіть модуль вектора
. Знайдіть модуль вектора 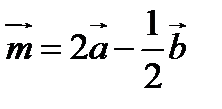 .
.
25. Розв’яжіть рівняння  .
.
26. Розв’яжіть рівняння 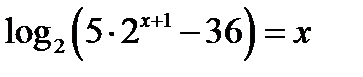 .
.
27. Точки  є вершинами трикутника. Знайдіть кут ABC.
є вершинами трикутника. Знайдіть кут ABC.
28. Обчисліть 
29. Тіло рухається прямолінійно зі швидкістю  (м/с). Зайдіть шлях, який пройшло тіло від початку до зупинки.
(м/с). Зайдіть шлях, який пройшло тіло від початку до зупинки.
30. Складіть рівняння дотичної до графіка функції  в точці з абсцисою
в точці з абсцисою  .
.
31. Розв’яжіть рівняння 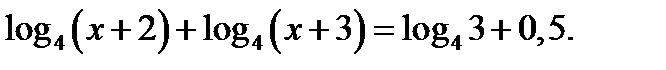
32. Знайдіть нулі функції 
33. Знайдіть площу фігури, обмеженої лініями  і
і 
34. Розв’яжіть рівняння 
35. Розв’яжіть рівняння 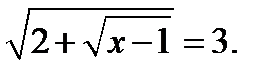
36. Знайдіть область визначення функції 
37. Обчисліть інтеграл 
38. Розв’яжіть рівняння 
39. З точки A до площини α проведено похилі AB і AC та перпендикуляр AK; AB =10 см; BK = 6 см; KC = 15 см. Знайдіть AC.
40. Знайдіть визначений інтеграл 
41. Знайдіть кут, що утворює дотична до графіка функції 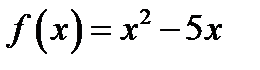 у точці з абсцисою 3 з додатним напрямом осі Ох.
у точці з абсцисою 3 з додатним напрямом осі Ох.
42. Знайдіть критичні точки функції 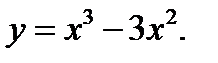
43. Знайти площу фігури, обмеженої лініями 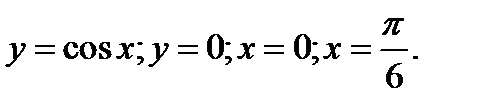
44. Для функції 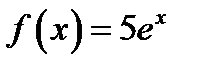 знайдіть первісну, графік якої проходить через точку М (0; – 2).
знайдіть первісну, графік якої проходить через точку М (0; – 2).
45. З точки A до площини α проведено похилі AB і AC та перпендикуляр AK; AB =10 см; BK = 6 см; KC = 15 см. Знайдіть AC.
46. Відстані від точки М до всіх вершин квадрата дорівнюють по 13 см, а до площини квадрата – 12 см. Знайдіть діагональ квадрата.
47. Похила утворює з площиною кут  . Знайти довжину похилої, якщо довжина її проекції на площину дорівнює
. Знайти довжину похилої, якщо довжина її проекції на площину дорівнює  см.
см.
48. На яких проміжках функція 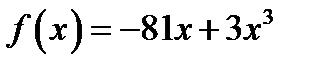 спадає?
спадає?
49. Знайдіть кутовий коефіцієнт дотичної до графіка функції  у точці
у точці 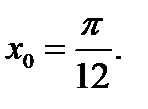
50. Знайдіть кутовий коефіцієнт дотичної до графіка функції 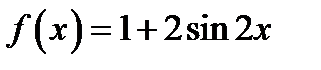 у точці
у точці 
51. Знайдіть кутовий коефіцієнт дотичної до графіка функції  у точці
у точці 
52. Розв’яжіть рівняння 
53. Розв’яжіть рівняння 
54. Розв’яжіть рівняння 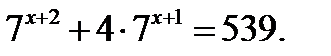
55. Знайдіть корені рівняння 
56. Знайдіть корені рівняння 
57. Розв’яжіть нерівність 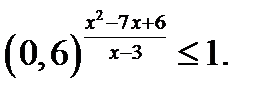
58. Розв’яжіть нерівність 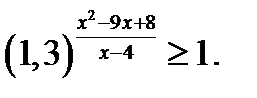
59. Розв’яжіть нерівність 
60. Спростіть вираз 
61. Спростіть вираз 
62. Спростіть вираз 
63. Спростіть вираз 
64. Розв’яжіть рівняння 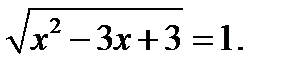
65. Розв’яжіть рівняння 
66. Розв’яжіть систему 
67. Розв’яжіть систему 
68. Знайдіть похідну функції 
69. Знайдіть похідну функції 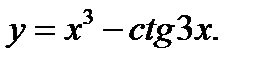
70. Знайдіть похідну функції 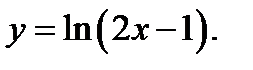
71. Розв’яжіть нерівність 
72. Розв’яжіть рівняння 
73. Розв’яжіть рівняння 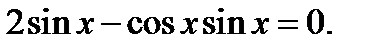
74. Знайдіть область визначення функції 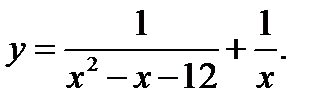
75. Знайдіть область визначення функції 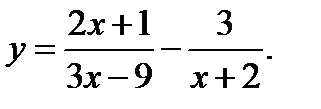
76. Знайдіть одну з первісних для функції 
77. Знайдіть одну з первісних для функції 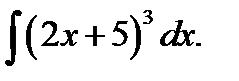
78. Із точки до площини проведено перпендикуляр і похилу. Довжина проекції похилої дорівнює 6 см. Знайдіть довжини перпендикуляра й похилої, якщо кут між ними дорівнює  .
.
79. З вершини С квадрата АВСD проведено пряму МС, перпендикулярну до площини квадрата. Обчисліть відстань від точки М до прямої ВD, якщо МС =1см, СD = 4 см.
80. Точка S рівновіддалена від сторін ромба АВСD і розташована на відстані 12 см від площини ромба. Знайдіть відстань від точки S до сторін ромба, якщо висота ромба дорівнює 10 см.
ІІІ рівень
1. Обчисліть значення виразу 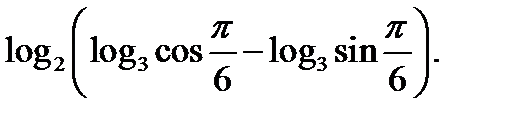
2. Знайти найменше та найбільше значення функції 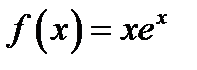 на проміжку
на проміжку 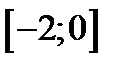 .
.
3. Знайдіть найбільше значення виразу  .
.
4. Знайти точки екстремуму функції 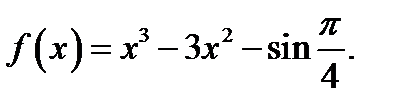
5. Знайдіть площу фігури, обмеженої лініями  та
та 
6. Знайдіть площу фігури, обмеженої лініями  та
та  .
.
7. Знайдіть похідну функції 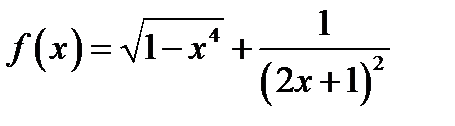
8. Розв’яжіть рівняння  .
.
9. Розв’яжіть рівняння 
10. Розв’яжіть рівняння 
11. Знайдіть проміжки зростання і спадання функції 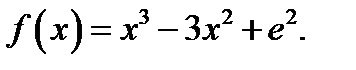
12. Порівняйте числа 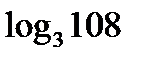 та
та  .
.
13. Обчисліть 
14. Обчисліть 
15. З точки А до площини проведено дві рівні похилі по 4 см кожна. Кут між похилими дорівнює 60  , а кут між їхніми проекціями – прямий. Знайдіть відстань від точки А до площини
, а кут між їхніми проекціями – прямий. Знайдіть відстань від точки А до площини  .
.
16. Розв’яжіть рівняння 
17. Для функції  знайдіть первісну, графік якої проходить через точку А
знайдіть первісну, графік якої проходить через точку А 
18. Дослідіть на монотонність та екстремум функцію: 
19. Знайдіть проміжки монотонності та точки екстремуму функції: 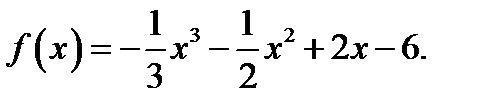
20. Знайдіть проміжки зростання функції 
21. Обчисліть: 
22. Обчисліть 
23. Знайти найменше та найбільше значення функції 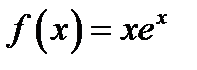 на проміжку
на проміжку 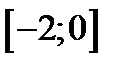 .
.
24. Знайдіть область визначення функції 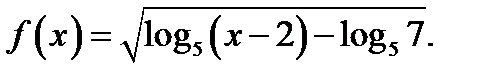
25. 3найдіть область визначення функції 
26. При яких значеннях х похідна функції  додатна?
додатна?
27. При яких значеннях х похідна функції  від’ємна?
від’ємна?
28. Відстані від точки М до всіх вершин квадрата дорівнюють по 13 см, а до площини квадрата – 12см. Знайдіть діагональ квадрата.
29. З точки А, взятої поза площиною α, проведено до неї дві похилі. Знайдіть довжини похилих, якщо одна з них на 13 см більша другої, а проекції похилих на площину α дорівнюють 6 і 20 см.
30. Із деякої точки проведено до даної площини дві похилі. Знайдіть довжини похилих, якщо проекції похилих дорівнюють 2 і 14 см, а похилі відносяться як 1:2.
31. Відстань від точки М до кожної вершини правильного трикутника дорівнює 10 см. Знайти відстань від точки М до площини трикутника, якщо медіана трикутника дорівнює 9 см.
32. Із точки, віддаленої від площини на відстані 10 см, проведено дві похилі, які утворюють з площиною кути в 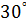 , а між собою кут в
, а між собою кут в  . Знайдіть відстань між кінцями похилих.
. Знайдіть відстань між кінцями похилих.
33. Із деякої точки простору проведено дві похилі, проекції яких дорівнюють 8 і 20 см. Знайти довжини похилих, якщо відомо що їх різниця дорівнює 8 см.
34. Відстані від точки S до всіх вершин правильного трикутника дорівнюють по 5 см, а до площини трикутника−3 см. Знайдіть висоту трикутника.
35. Дано координати точок А(0;2;-4), В(1;7;-2), С(2;4;-7). Знайти кут між векторами 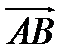 і
і  .
.
36. Дано координати точок А(0;3;-1), В(0;2;-1), С(2;4;-3). Знайти кут між векторами 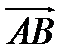 і
і  .
.
37. Точка S рівновіддалена від сторін квадрата ABCD і розташована на відстані 2 см від площини квадрата. Знайдіть відстань від точки S до сторони квадрата, якщо сторона квадрата дорівнює 2 см.
38. Відстань від точки М до всіх вершин квадрата дорівнює 5 см. Знайдіть відстань від точки М до площини квадрата, якщо діагональ квадрата дорівнює 6 см.
39. Площа рівностороннього трикутника дорівнює  . Знайдіть відстань від площини трикутника до точки, віддаленої від усіх його вершин на 13 см.
. Знайдіть відстань від площини трикутника до точки, віддаленої від усіх його вершин на 13 см.
40. Знайдіть довжину перпендикуляра, якщо довжина похилої становить 17 см, а її проекція на площину – 15 см.
41. Верхні кінці двох вертикальних стовпів, розташованих на відстані 1 м один від одного, з’єднані поперечиною. Висота одного стовпа дорівнює 3,4 м, а другого – 1м. знайдіть довжину поперечини.
42. Точка F розташована на відстані 6 см від вершин прямокутника й на відстані 4 см від його площини. Знайдіть сторони прямокутника, якщо одна з них у два рази більша за іншу.
43. Менша основа прямокутної трапеції дорівнює 9 см, більша діагональ – 17 см, а висота – 8 см. Чому дорівнює периметр трапеції?
44. Основи трапеції дорівнюють 16 см і 10 см. Чому дорівнює відстань між серединами її діагоналей?
45. Сторони трикутника дорівнюють 29 см, 25 см і 6 см. Знайдіть висоту трикутника, проведену до його меншої сторони.
Не нашли, что искали? Воспользуйтесь поиском: