
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ. Разделы и темы для самостоятельного изучения Виды и содержание самостоятельной работы 1 курс Тема 1
| Разделы и темы для самостоятельного изучения | Виды и содержание самостоятельной работы |
| 1 курс | |
| Тема 1. Предел и непрерывность функции | Тема 1. Предел и непрерывность функции.
§1. Множество действительных чисел. Понятие функции. Способы задания функций. Элементарные функции. Простейшие неэлементарные функции.
Литература:[1, гл. 5], [2, гл. VI], [3, гл. V], [4, § 1.1 – 1.2, стр. 5–9] [5, гл. V, § 1],
[7, гл. 1, гл. 4, §1].
Упражнения:[5, упр. 679, 700],
[6, упр. 1.1. 1), 2), 5) – 7), 1.2. 1) – 3)], [7, гл. 4, упр. 73, 75, 83, 99, 139, 191].
§2. Числовая последовательность и ее предел. Предел функции. Основные теоремы о пределах. Бесконечно малые и бесконечно большие функции. Односторонние пределы. Два замечательных предела.
Литература:[1, гл. 6, § 4 – 10], [2, гл. VII, § 1 – 13], [3, гл. VI, § 24 – 28], [4, § 1.2 – 1.6, стр. 9–19], [5, гл. V, § 2 – 7, 10], [7,гл. 4 § 2].
Упражнения:[5, упр. 730, 734, 736, 742, 743, 763, 770, 779, 782 – 785], [6, упр. 1.20 – 1.25, 136 – 139, 146 – 149],
[7, гл. 4, упр. 228, 234 – 241, 264 – 267, 289].
§3. Приращение функции. Возрастание и убывание функции. Непрерывность функции. Точки разрыва функции и их классификация. Свойства непрерывных функций.
Литература:[1, гл. 6, § 1 – 3], [2, гл. VIII],
[3, гл. VI, § 29], [4, § 1.7, стр. 19–24],
[5, гл. V, § 8], [7, гл. 4, § 2]
Упражнения:[5, упр. 814 – 816], [6, упр. 1.72, 1.81, 1.83, 1.86], [7, гл. 4, упр. 225 – 226].
контрольные вопросы
Тема 1..Сформулируйте определение понятия функции. Что называется областью определения функции?
2. Какие функции называются элементарными?
3. Какой вид имеют графики функций 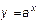 при при 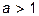 , , 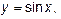 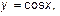  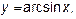 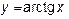 ? Укажите области определения и множества значений этих функций. Какие из этих функций являются чётными?
4. При каких условиях число ? Укажите области определения и множества значений этих функций. Какие из этих функций являются чётными?
4. При каких условиях число 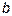 называется пределом функции называется пределом функции 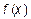 при стремлении при стремлении  к числу 2, к бесконечности к числу 2, к бесконечности 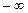 , , 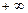 ? Прочитайте формулы ? Прочитайте формулы  , , 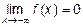 и объясните их смысл.
5. Пределом какой функции при и объясните их смысл.
5. Пределом какой функции при  является число является число 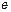 ? Найдите в учебнике значение числа ? Найдите в учебнике значение числа 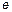 с двумя знаками после запятой. Как называется и обозначается логарифм числа с двумя знаками после запятой. Как называется и обозначается логарифм числа 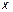 по основанию по основанию 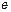 ? Какому числу равен предел ? Какому числу равен предел  ?
7. Какие правила применяются при вычислении пределов суммы, разности и отношения двух функций?
8. Как определяется непрерывность функции ?
7. Какие правила применяются при вычислении пределов суммы, разности и отношения двух функций?
8. Как определяется непрерывность функции 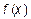 в точке в точке 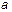 ? ?
|
| Тема 2. Дифференциальное исчисление функций одной переменной | Тема 2. Дифференциальное исчисление функции одной переменной §1. Определение производной. Дифференцируемость и непрерывность функций. Геометрический, физический и экономический смысл производной. Свойства производной. Правила дифференцирования (включая производные сложной и обратной функции). Литература:[1, гл. 7], [2, гл. IX, X], [3, гл. VII, § 30 – 37], [4, § 1.8, 1.10, 1.11, стр. 25–27, 30–40], [5, гл. VI, § 1, 2,4 – 6, 8–10; гл. VII, § 1], [7, гл. 5, § 1, 2]. Упражнения:[5, упр. 849, 850, 852–854, 874–877, 937–939, 980–985, 1090–1092], [6, упр. 2.1, 2.2, 2.7–2.17, 2.21–2.24, 2.76–2.79, 2.111, 2.112, 2.231, 2.232], [7, гл. 5, упр. 1, 11 – 13, 25–30, 33–36, 45–50, 136, 137]. § 2. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя. Литература:[1, гл. 9, § 1], [2, гл. XI, упр. 1, 2, 5], [3, гл. VIII, § 40, 41], [4, § 1.13, 1.14.1, стр. 41–45], [5, гл. VII, § 2, 3] [7, гл. 5, § 6]. Упражнения:[5, упр. 1101–1107, 1122–1134], [6, упр. 2.162–2.164, 2.166–2.168, 2.171, 2.173–2.183], [7, гл. 5, § 6, упр. 225–234, 241, 244, 246, 260]. §3. Дифференциал функции, его связь с производной. Геометрический смысл дифференциала и его использование в приближенных вычислениях. Производные и дифференциалы высших порядков. Литература:[1, гл. 8], [2, гл. XII], [3, гл. VII, § 38], [4, § 1.9, 1.12, 1.14.4, стр. 27–30, 39–40, 55–56], [5, гл. VI, § 11] [7, гл. 5, § 3, 4]. Упражнения:[5, упр. 1064, 1070, 1071, 1021, 1022], [6, упр. 2.122–2.124, 2.134–2.137, 2.146, 2.147, 2.156], [7, гл. 5, упр. 146, 160, 161, 163–167, 174, 175, 179, 198, 199]. §4. Исследование функций с помощью дифференциального исчисления. Условия возрастания и убывания функций. Экстремум функции. Необходимые и достаточные условия существования экстремума. Литература:[1, гл. 9, § 2 –5], [2, гл. XI, § 2, упр. 3 – 5, §7, упр. 6 – 14], [3, гл. VII, § 42 – 44], [4, § 1.14.2, стр. 46–55] [5, гл. VII, § 4, 5], [7, гл. 5, § 7]. Упражнения:[5, упр. 1158, 1160–1162, 1176], [6, упр. 2.203] [7, гл. 5, упр. 282]. §5. Выпуклость графика функции. Точки перегиба и их нахождение. Асимптоты. Общая схема исследования функции. Литература:[1, гл. 9, § 6 –8], [2, гл. XI, § 8, 10, упр. 15 – 27], [3, гл. VII, § 45, 46], [5, гл. VII, § 6; гл. V, §9], [7, гл. 5, § 7]. Упражнения:[6, упр. 2.204–2.207, 2.224–2.226, 2.233, 2.234], [7, гл. 5, упр. 297–300, 324–327]. §6. Формулы Тейлора и Маклорена. Примеры разложения элементарных функций по формуле Маклорена. Литература:[4, § 1.4.14, стр. 56–57], [7, гл. 5, § 6]. Упражнения:[7, гл. 5 упр. 269–271]. контрольные вопросы Тема 2.. Сформулируйте определение производной. Каков геометрический смысл производной? 2. Функция имеет производную в данной точке. Следует ли отсюда, что она непрерывна в этой точке? 3. Сформулируйте теоремы Ролля и Лагранжа. Каков геометрический смысл этих теорем? Сформулируйте теорему Коши. 4. В чем заключается правило Лопиталя? При каких условиях применяется правило Лопиталя? Перечислите различные типы неопределённостей, для раскрытия которых может быть использовано это правило. Приведите примеры. 5. Что называется дифференциалом функции? Приведите примеры. 6. Каковы признаки возрастания и убывания функции? 7. Что такое экстремум функции? Каковы необходимые и достаточные условия экстремума? Приведите примеры. 8. Приведите пример, показывающий, что обращение производной в нуль не является достаточным условием экстремума. 9. Как найти интервалы выпуклости и точки перегиба графика функции? Приведите примеры. |
Продолжение табл.
| Тема 3. Дифференциальное исчисление функций нескольких переменных | Тема 3. Дифференциальное исчисление функций нескольких переменных Понятие функции нескольких переменных. Предел и непрерывность функций нескольких переменных. Полное и частное приращение функций. Частные производные. Дифференцируемость и дифференциал функции. Геометрический смысл дифференцируемости функций двух переменных. Производная по направлению. Градиент и его свойства. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие для случая двух независимых переменных. Нахождение наибольшего и наименьшего значения функции нескольких переменных. Условный экстремум. Метод множителей Лагранжа. Метод наименьших квадратов. Литература:[1, гл. 10], [2, гл. XX], [4, гл. 3, стр. 58–72], [5, гл. XI, § 1 – 3, 6, 11, 12], [7, гл. 11, 12]. Упражнения:[5, 1858‑1861, 1884, 1885, 1927, 1931, 1947, 2018, 2025, 2030–2033, 2036, 2037], [6, 3.1, 3.4, 3.4–3.7, 3.14–3.17, 3.23–3.26, 3.29–3.33, 3.36, 3.38–3.39, 3.40–3.46, 3.51–3.53], [7, гл. 12 упр. 1–4, 34, 46, 51, 59, 109–111]. Тема 3. 1. Сформулируйте определение частных производных. 2. Что называется полным приращением и полным дифференциалом функции двух переменных? Приведите примеры. 3. Каковы достаточные условия минимума (максимума) функции двух переменных. Что такое условный экстремум? |
| Тема 4. Интегралы | Тема 4. Интегралы
§1. Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов. Основные методы интегрирования: замена переменной, интегрирование по частям.
Литература:[1, гл. 11], [2, гл. XIII], [3, гл. IX], [4, § 2.1 – 2.5, стр. 73–82], [5, гл. VIII, § 1 – 8, 10], [7, гл. 6, § 1–3].
Упражнения:[5, 1263‑1267, 1279–1284, 1291–1296, 1301, 1305, 1307, 1309, 1330, 1340, 1362, 1363, 1375–1379, 1383, 1428, 1444], [6, 4.1–4.5, 4.19–4.22, 4.61–4.65, 4.68–4.72, 4.80, 4.96–4.99, 4.104, 4.105], [7, гл. 6 упр. 1–5, 37–40, 56–59, 102–105, 107–110, 118, 119, 126].
§2. Определенный интеграл как предел интегральных сумм. Свойства определенного интеграла. Формула Ньютона‑Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.
Литература:[1, гл. 12, §5], [2, гл. XIV, §12, упр. 10], [3, гл. X, §59], [4, § 2.6 – 2.9, стр. 82–88], [5, гл. IX, § 7], [7, гл. 6, § 4].
Упражнения:[5, 1593‑1596, 1601], [6, 4.117, 4.118, 4.120–4.124, 4.129, 4.130, 4.136], [7, гл. 6 упр. 254–257, 268–270].
§3. Геометрические приложения определенного интеграла: площадь плоской фигуры, объем тела вращения. Приближенные методы вычисления определенного интеграла: формулы прямоугольников, трапеций, Симпсона.
Литература:[1, гл. 12, §6, 8], [2, гл. XV], [3, гл. X, § 58], [4, § 2.10, 2.12, стр. 88–92, 95–97], [5, гл. IX, § 2–3], [7, гл. 6, § 5].
Упражнения:[5, упр. 1625, 1653, 1654, 1669, 1670], [6, 4.138, 4.142 ‑‑ 4.146, 4.158], [7, гл. 6 упр. 290, 292–294, 219, 221, 388, 391].
§4. Несобственные интегралы. Понятие о кратных интегралах.
Литература:[1, гл. 12, §5], [2, гл. XIV, §12, упр. 10], [3, гл. X, §59], [4, § 2.11, 2.13, стр. 92–95, 97–99], [5, гл. IX, § 7], [7, гл. 6, § 6].
Упражнения: [5, упр. 1748, 1752], [6, упр. 4.171], [7, гл. 6 упр. 355–358].
Тема 4. 1. Сформулируйте определение первообразной функции. Докажите, что любые две первообразные одной и той же функции отличаются на константу.
2. Что называется неопределённым интегралом?
3. Какие правила применяются для вычисления неопределённого интеграла суммы функций, для вычисления 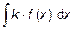 ?
4. Выведите формулу интегрирования по частям.
5. Что называется интегральной суммой функции ?
4. Выведите формулу интегрирования по частям.
5. Что называется интегральной суммой функции 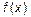 на отрезке на отрезке 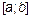 . Какая фигура называется криволинейной трапецией? По какой формуле вычисляется её площадь?
6. Напишите формулу Ньютона-Лейбница.
7. Какие свойства определённого интеграла Вам известны?
8. В чём состоят определение и геометрический смысл несобственного интеграла с бесконечным пределом интегрирования? . Какая фигура называется криволинейной трапецией? По какой формуле вычисляется её площадь?
6. Напишите формулу Ньютона-Лейбница.
7. Какие свойства определённого интеграла Вам известны?
8. В чём состоят определение и геометрический смысл несобственного интеграла с бесконечным пределом интегрирования?
|
| Тема 5. Дифференциальные уравнения | Тема 5. Дифференциальные уравнения
§1. Понятие о дифференциальном уравнении. Примеры торгово-экономических задач, приводящие к дифференциальным уравнениям. Порядок дифференциального уравнения. Семейство решений. Теорема существования и единственности решения (без доказательства). Задача Коши. Геометрическое истолкование решения. Общее и частное решение дифференциального уравнения.
Уравнения с разделяющимися переменными. Линейное уравнение первого порядка. Возможные случаи понижения порядка дифференциального уравнения (на примере уравненийвторогопорядка), когда в его записи отсутствуют независимая переменная или искомая функция.
Литература:[1, гл. 13, § 5], [2, гл. XXI, §1 – 5, 9], [3, гл. XVI, §79], [4, § 2.14 – 2.17, стр. 99–108], [5, гл. XII, § 1 –3, 7, 10], [7, гл. 14, § 1.1–1.3].
Упражнения: [5, упр. 2051, 2057, 2058, 2061, 2115, 2116], [6, упр. 5. 14–5.18, 5.21], [7, гл. 6, упр. 1–4, 10–13, 20–23, 43–46].
§2. Линейные дифференциальные уравнения второго порядка. Структура общего решения. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение. Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Подбор частных решений при специальном виде правой части.
Литература:[1, гл. 14], [2, гл. XXII, § 7, 11 – 13], [3, гл. XVI, §80], [4, § 2.18–2.21, стр. 108–118], [5, гл. XII, § 8, 9], [7, гл. § 2].
Упражнения:
[5, упр. 2184 – 2187, 2213 – 2216, 2218], [6, упр. 5.22, 5.23, 5.25, 5.27, 5.29, 533, 5.37–5.39], [7, гл. 6, упр. 78‑‑79, 84–87, 98–101, 104–106].
Тема 5. 1. Что называется решением дифференциального уравнения? Что является неизвестной в дифференциальном уравнении? Что называется порядком дифференциального уравнения?
2. Как из общего решения дифференциального уравнения первого (второго) порядка можно получить его частное решение? Каков геометрический смысл начальных условий дифференциальных уравнений первого и второго порядка?
3. В чем заключается смысл теоремы о существовании и единственности решения для дифференциального уравнения первого порядка? Приведите пример дифференциального уравнения первого порядка, графики двух различных решений которого пересекаются в некоторой точке. Выполняются ли в этой точке условия теоремы существования и единственности?
4. При каких условиях дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными?
5. Как решаются линейные дифференциальные уравнения первого порядка?
6. В каких случаях линейное дифференциальное уравнение второго порядка называется однородным, неоднородным?
7. Напишите характеристический многочлен уравнения 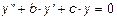 . Пусть . Пусть 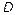 – дискриминант характеристического многочлена. Какой вид имеет общее решение этого дифференциального уравнения при – дискриминант характеристического многочлена. Какой вид имеет общее решение этого дифференциального уравнения при 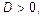 при при 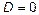 и при и при 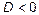 ?
8. Какова структура общего решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами? ?
8. Какова структура общего решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?
|
| Тема 6. Ряды | Тема 6. Ряды
§1. Числовые ряды. Сходимость ряда. Сумма ряда Свойства рядов. Необходимое условие сходимости ряда. Теорема сравнения.Признаки сходимости Даламбера, Коши. Знакочередующиеся ряды. Абсолютная и условная сходимость. ПризнакЛейбница.
Литература:[1, гл. 15], [2, гл. XXI, § 1 – 7], [3, гл. XI], [4, § 2.22 – 2.26, стр. 118–130], [5, гл. XIV, § 1], [7, гл. 8, § 1–3].
Упражнения: [5, упр. 2422–2424, 2432, 2433, 2435, 2437], [6, упр. 6.1, 6.15–6.18, 6.24, 6.39–6.42], [7, гл. 8, упр. 31‑‑34, 43–48].
§2. Степенные ряды. Радиус, интервал и область сходимости. Разложение элементарных функций в ряд Маклорена или Тейлора.
Литература:[1, гл. 16, § 1 – 5], [2, гл. XXI, § 8 – 12, 14], [3, гл. XII, 65 – 68], [4, § 2.27 – 2.29, стр. 130–137], [5, гл. XIV, § 3 – 4], [7, гл. 8, § 4].
Упражнения: [5, упр. 2483 – 2486, 2492. 2), 3)], [6, упр. 6.77–6.80, 6.97, 6.111, 6.115, 6.98], [7, гл. 8, упр. 103‑‑106, 119–122].
§3. Использование рядов для приближенных вычислений.
Литература:[1, гл. 16, § 6], [2, гл. XXI, § 13], [3, гл. XII, § 69], [4, § 2.29, стр. 137–139], [5, гл. XIV, § 5].
Упражнения: [5, упр. 2512, 2518, 2520], [6, упр. 6.125–6.127].
Тема 6. 1. Что называется суммой сходящегося степенного ряда?
2. Почему при исследовании сходимости ряда можно отбрасывать любое конечное число его членов?
3. Можно ли утверждать, что ряд сходится, если предел его общего члена равен нулю?
4. Сформулируйте признак Даламбера и интегральный признак Коши сходимости ряда. Сформулируйте теорему сравнения рядов.
5. Какие знакопеременные ряды называются абсолютно сходящимися и какие – условно сходящимися? Сформулируйте признак Лейбница.
6. Приведите примеры степенных рядов, имеющих нулевой, конечный и бесконечный радиус сходимости.
7. Выпишите разложения в ряд Маклорена функций: 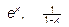 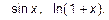 Каковы области сходимости получившихся рядов? Каковы области сходимости получившихся рядов?
|
| Тема 7. Векторная алгебра | Проработка учебной и научной литературы [[1,4,6,9,10,12,13,14,15] Решение задач, упражнений из учебно-методической литературы:[2] Упр.1.2.1, 1.2.2, 1.2.3, 1.2.4, 1.2.5, 1.2.8, 1.2.10 |
| Тема 8. Элементы аналитической геометрии | Проработка учебной и научной литературы [1,4,6,9,10,12,13,14,15] Решение задач, упражнений из учебно-методическая литературы [2] Упр.2.1.1, 2.2.2, 2.2.3, 2.2.4, 2.2.5, 2.2.8, 2.2.10 |
| Тема 9. Матрицы и определители | Проработка учебной и научной литературы [1,4,6,9,10,12,13,14,15] Решение задач, упражнений из учебно-методической литературы [2] Упр.1.26, 1.2.7,1.3.7, 1.3.8, 1.3.9, 1.3.10, |
| Тема 10. Системы линейных уравнений (СЛУ) | Проработка учебной и научной литературы [1,4,6,9,10,12,13,14,15] Решение задач, упражнений из учебно-методическая литературы [2] Упр.1.3.15, 1.3.16 |
| Тема 11. Системы линейных неравенств | Проработка учебной и научной литературы литературы [1,4,6,9,10,12,13,14,15] Решение задач, упражнений из учебно-методической литературы:[2,3,4] |
| Тема 12. Основные понятия теории вероятностей. Случайные события | Проработка учебной и научной литературы [2,3,4,7,16,17,19,21,23,24,25] Решение задач, упражнений из учебно-методической литературы:[2] Упр.3.1.1, 3.1.2, 3.1., 3.1.4, 3.1.5, 3.1..8, 3.1.10 |
| Тема 13. Случайные величины и их числовые характеристики | Проработка учебной и научной литературы [2,3,4,7,16,17,19,21,23,24,25] Решение задач, упражнений из учебно-методической литературы:[2] Упр.3.2.1, 3.2.2, 3.2.3, 3.2.4, 3.2.5, 3.2.8, 3.2.10 |
| Тема 14. Основные распределения случайных величин | Проработка учебной и научной литературы [2,3,4,7,16,17,19,21,23,24,25] Решение задач, упражнений из учебно-методической литературы:[2] Упр.3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5, 3.4.8, 3.4.10 |
| Тема 15. Функция случайной величины | Проработка учебной и научной литературы [2,3,4,7,16,17,19,21,23,24,25] Решение задач, упражнений из учебно-методической литературы:[2] Упр.3.6.1, 3.6.2, 3.6.3, 3.6.4, 3.6.5, 3.6.7, 3.6.10 |
| Тема 16. Случайные векторы | Проработка учебной и научной литературы [2,3,4,7,16,17,19,21,23,24,25] Решение задач, упражнений из учебно-методической литературы:[2] Упр.3.7.1, 3.7.2, 3.7.3, 3.7.4, 3.7.5, 3.7.7, 3.7.10 |
| Тема 17. Закон больших чисел и предельные теоремы | Проработка учебной и научной литературы [2,3,4,7,16,17,19,21,23,24,25] Решение задач, упражнений из учебно-методической литературы:[2] Упр.3.8.1, 3.8.2, 3.8.3, 3.8.4, 3.8.5, |
| 2 курс | |
| Тема 18. Задача линейного программирования | Проработка учебной и научной литературы:
[4, 5, 8, 11]
Решение задач, упражнений из учебно-методической литературы
[ 3.4]
Контрольные вопросы для проверки усвоения материала
1. Как записать уравнение отрезка прямой?
2. Что такое выпуклая линейная комбинация точек?
3. Что такое угловая точка множества?
4. Какое множество называется выпуклым, замкнутым. ограниченным?
5. Что такое многоугольник и многогранник?
6. Сформулировать теорему о выпуклости многоугольника.
7. Сформулировать теорему о виде области допустимых решений задачи.
8. Сформулировать теорему об экстремуме целевой функции.
9. Какое решение называется опорным и что называется его базисом?
10. Сформулировать теоремы о взаимосвязи опорного решения и угловых точек области допустимых решений.
11. В чём состоит идея симплексного метода.
12. Как найти начальное опорное решение и перейти от одного опорного решения к другому.
Примеры
Пример 1. 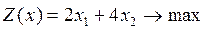
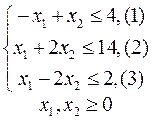 Пример 2.
Пример 2. 
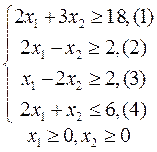 Пример 3.
Пример 3. 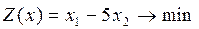
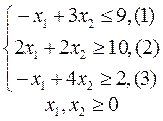 4.
4. 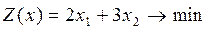
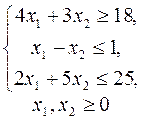 5.
5. 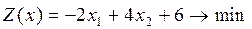
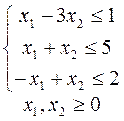 6.
6. 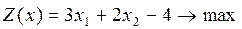
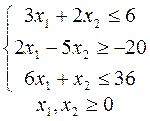 7.
7. 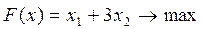
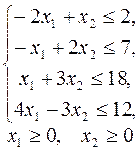 8.
8. 
 9.
9. 
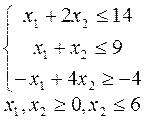 10.
10. 
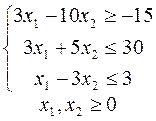 11.
11. 
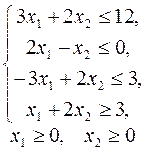 12.
12. 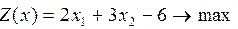
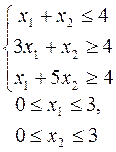 13.
13. 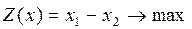
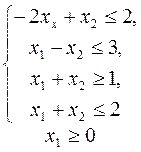 14.
14. 
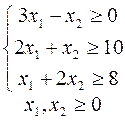 15.
15. 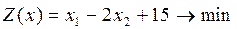
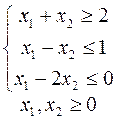 16.
16. 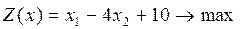
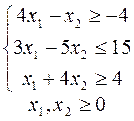 17.
17. 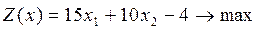
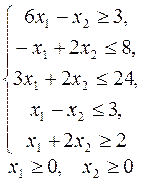 Задача с n-переменными
Упражнения
1.
Задача с n-переменными
Упражнения
1.
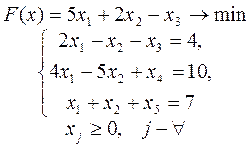 2.
2.
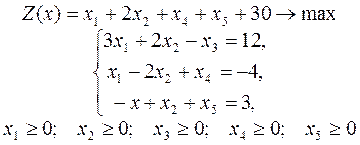 3.
3.
 4.
4.
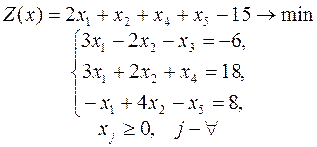 5.
5.
 6.
6.
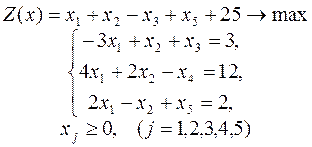
|
| Тема 19. Симплексный метод линейного программирования |
Проработка учебной и научной литературы:
[4, 5, 8, 11]
Решение задач, упражнений из учебно-методической литературы
[ 3.4]
Контрольные вопросы для проверки усвоения материала
1. Вывести формулу преобразования целевой функции при переходе от одного опорного решения к другому.
2. Записать формулу для расчёта оценок разложений векторов условий по базису опорного решения в координатном и векторном виде. к оптимальному решению.
3. Записать условие для наискорейшего приближения
4. Записать признак оптимальности опорного решения.
5. Записать условие существования единственного оптимального решения.
6. Записать условие существования бесконечного множества оптимальных решений.
7. Записать условие отсутствия оптимального решения ввиду неограниченности целевой функции.
8. В чём состоит алгоритм симплексного метода?
Пример. 1.Решить симплекс-методом задачу:
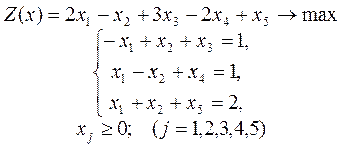 Пример 2
Пример 2
 3.
3.
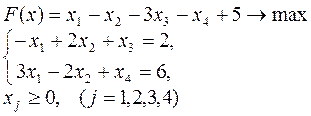 4.
4.
 5.
5.
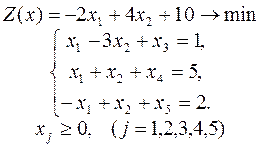 6.
6.
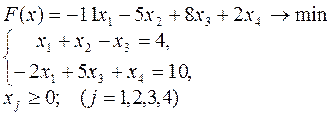 7.
7.
 8.
8.
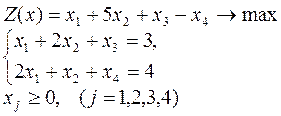 9.
9.
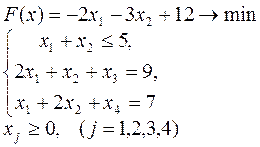 10.
10.
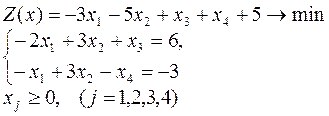 11.
11.
 Литература:
[4, 5, 8, 11]
Учебно-методическая литература [ 3.4]
Литература:
[4, 5, 8, 11]
Учебно-методическая литература [ 3.4]
|
| Тема 20. Двойственность в линейном программировании | Проработка учебной и научной литературы: [4, 5, 8, 11] Решение задач, упражнений из учебно-методической литературы [ 3.4] Упр.4.1.1, 4.1.2, 4.1.3, 4.1.4, 4.1.5, 4.1.8, 4.1.10 Контрольные вопросы для проверки усвоения материала 1. Что такое двойственные (сопряженные) задачи линейного программирования? 2. Привести пример составления пары двойственных задач. 3. Почему переменные двойственной задачи называются оценками? 4. Сформулировать правило составления математической модели двойственной задачи. 5. Записать симметричные и несимметричные пары двойственных задач. 6. Сформулировать первую теорему двойственности. 7. Записать формулы для нахождения оптимального решения двойственной задачи по результатам нахождения оптимального решения исходной задачи. 8. Сформулировать вторую теорему двойственности. 9. Записать условие оптимальности допустимых решений пары двойственных задач. 10. Каким образом связаны координаты оптимального решения исходной задачи и уравнения системы ограничений двойственной задачи. |
| Тема 21. Транспортная задача | Проработка учебной и научной литературы: [4, 5, 8, 11] Решение задач, упражнений из учебно-методической литературы [ 3.4] Контрольные вопросы для проверки усвоения материала 1. Дать текстовую формулировку транспортной задачи. 2. Записать математическую модель транспортной задачи. 3. Сформулировать необходимые и достаточные условия разрешимости тзлп. 4. Чему равен ранг системы векторов условий транспортной задачи? 5. Что такое цикл и как он связан с опорным решением? 6. Как проверить линейную независимость векторов условий тзлп. 7. Доказать то, что решения, построенные по методу северо-западного угла и минимальной стоимости являются опорными. 8. Сформулировать теорему о существовании и единственности цикла. 9. Как построить цикл? 10. Что такое означенный цикл и сдвиг по циклу? 11. В чём состоит распределительный метод и критерий его оптимальности? 12. Доказать признак оптимальности метода потенциалов. 13. В чём особенности решения задачи с неправильным балансом? 14. Как решается тзлп с ограничениями на пропускные возможности? Литература (3,4) Упр.3.1.1, 51.2, 5.1.3, 5.1.4, 5.1.5, 5.1.8, 5.1.10 |
| Тема 22. Матричные игры | Проработка учебной и научной литературы: [4, 5, 8, 11] Решение задач, упражнений из учебно-методической литературы [ 3.4] Упр.6.1.1, 6.1.2, 6.1.3, 6.1.4, 6.1.5, 6.1.8, 6.1.10 Вопросы для самопроверки 1.Опишите условия риска и неопределенности. 2.Приведите примеры конфликтов в коммерческой сфере. 3.Поясните, в чем состоит природа столкновения в торговле. 4.Поясните построение платежной матрицы. 5.Объясните построение матрицы рисков. 6. Назовите критерии принятия решения в условиях риска и неопределенности. |
| Тема 23. Потоки событий | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.7.1.1, 7.1.2, 7.1.3, 7.1.4, 7.1.5 ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 1. Перечислите задачи планирования в торговле. 2. Приведите существующие методы планирования в торговле. 3. Приведите пример экономико-математической постановки задачи планирования перевозки товаров. 4. Назовите категории оптимального планирования. 5. Приведите варианты изображения моделей постановки задач оптимального планирования. 6. Перечислите этапы моделирования по формированию оптимальных планов торговли. |
| Тема 24. Уравнения Колмогорова | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.1.1.1, 1.1.2, 1.1.3 |
| Тема 25. Системы массового обслуживания | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.1.1.10, 1.1.12, 1.1.13, 1.1.14, 1.1.15 Вопросы для самопроверки 1. Перечислите задачи обслуживания в торговле, критику и показатели успеха. 2. Приведите основные понятия, определения и показатели СМО. 3. Назовите структуры и классификации СМО. 4. Перечислите показатели эффективности СМО. 5. Назовите этапы экономико -математического моделирования задач обслуживания. 6. Представьте коммерческие организации и предприятия в виде СМО. 7. Приведите основные показатели и модели СМО с ограниченной длиной очереди. 8. Приведите основные показатели и модели СМО с ожиданием. 9. Представьте коммерческую сеть в виде совокупности СМО. |
| Тема 26. Задача динамического программирования | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.2.1.1, 2.1.2, 2.1.3, |
| Тема 27. Основы теории графов | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.3.1.1, 3.1.2, 3.1.3, 3.1.4 |
| Тема 28. Задача о коммивояжере | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.2.1.5, 2.1. 7 |
| Тема 29. Задача об оптимальном потоке | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.2.1.9 |
| Тема 30. Задача о назначениях | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.2.1.10 |
| Тема 31. Задача сетевого планирования | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] Упр.3.1.1, 3.1.2, 3.1.3, 3.1.4, 3.1.5 Вопросы для самопроверки 1. Назовите основные термины и определения СПУ. 2. Дайте определение критического пути. 3. Назовите критерии оптимизации сетевой модели. 4.Перечислите правила построения сетевого графика. 5. Что включает анализ сетевой модели? 6. В чем состоит содержание оптимизации сетевого графика? 7. Какой сетевой план является оптимальным? 8. Перечислите задачи коммерческой деятельности, пригодные для решения методами СПУ. |
| Тема 32. Эластичность и экономический анализ | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] |
| Тема 33. Функции полезности | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методи-ческой литературы:[6] |
| Тема 34. Производственные функции | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методи-ческой литературы:[6] |
| Тема 35. Функции спроса | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] |
| Тема 36. Моделирование экономического равновесия и динамики | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методической литературы:[6] |
| Тема 37. Модели управления запасами | Проработка учебной и научной литературы: [4,11] Решение задач, упражнений из учебно-методи-ческой литературы:[6] |
7. ТЕМЫ КОНТРОЛЬНЫХ РАБОТ
И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ
Не нашли, что искали? Воспользуйтесь поиском: