
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольные задания. 1–10. Даны координаты вершин пирамиды А1А2А3А4
1–10. Даны координаты вершин пирамиды А 1 А 2 А 3 А 4. Найти: 1) уравнение прямой, на которой лежит ребро А 1 А 2; 2) уравнение плоскости, на которой лежит грань А 1 А 2 А 3; 3) угол между ребром А 1 А 4 и гранью А 1 А 2 А 3; 4) площадь грани А 1 А 2 А 3; 5) объём пирамиды.
1. А 1(7, 7, 6), А 2(5, 10, 6), А 3(5, 7, 12), А 4(7, 10, 4).
2. А 1(6, 1, 1), А 2(4, 6, 6), А 3(4, 2, 0), А 4(1, 2, 6).
3. А 1(8, 7, 5), А 2(10, 6, 6), А 3(5, 7, 9), А 4(8, 11, 8).
4. А 1(7, 7, 3), А 2(6, 5, 8), А 3(3, 5, 8), А 4(8, 4, 1).
5. А 1(4, 2, 5), А 2(0, 7, 2), А 3(0, 2, 7), А 4(1, 5, 0).
6. А 1(4, 4, 10), А 2(4, 10, 2), А 3(2, 8, 4), А 4(9, 8, 9).
7. А 1(4, 6, 5), А 2(6, 9, 4), А 3(2, 10, 10), А 4(7, 5, 9).
8. А 1(3, 5, 4), А 2(8, 7, 4), А 3(5, 10, 4), А 4(4, 7, 8).
9. А 1(10, 6, 6), А 2(-2, 8, 2), А 3(6, 8, 9), А 4(7, 10, 3).
10. А 1(2, 9, 3), А 2(6, 3, 7), А 3(6, 8, 5), А 4(5, 11, 10).
11–20. Установить, какие линии определяются данными уравнениями. Изобразить линии на чертеже.
11. а)  , б)
, б) 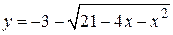 .
.
12. а)  , б)
, б)  .
.
13. а)  , б)
, б)  .
.
14. а)  , б)
, б) 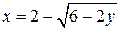 .
.
15. а)  , б)
, б) 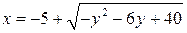 .
.
16. а)  , б)
, б)  .
.
17. а)  , б)
, б)  .
.
18. а)  , б)
, б)  .
.
19. а)  , б)
, б)  .
.
20. а)  , б)
, б) 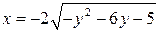 .
.
21–30. 1) Записать число  в алгебраической форме; 2) изобразить его на координатной плоскости; 3) записать число
в алгебраической форме; 2) изобразить его на координатной плоскости; 3) записать число  в тригонометрической и показательной формах; 4) вычислить
в тригонометрической и показательной формах; 4) вычислить 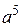 ; 5) найти все корни уравнения
; 5) найти все корни уравнения 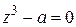 .
.
21. 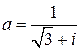 . 22.
. 22.  .
.
23.  . 24.
. 24.  .
.
25.  . 26.
. 26.  .
.
27. 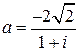 . 28.
. 28.  .
.
29.  . 30.
. 30.  .
.
31–40. Найти пределы, используя замечательные пределы и эквивалентные бесконечно малые функции.
31. а)  , б)
, б)  . 32. а)
. 32. а) 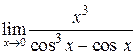 , б)
, б)  .
.
33. а)  , б)
, б)  . 34. а)
. 34. а)  , б)
, б)  .
.
35. а)  , б)
, б)  . 36.а)
. 36.а)  ,б)
,б)  .
.
37. а)  , б)
, б) 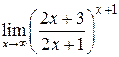 . 38. а)
. 38. а)  , б)
, б)  .
.
39. а)  , б)
, б)  . 40. а)
. 40. а)  , б)
, б)  .
.
41–50. Дано уравнение 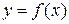 кривой, точка
кривой, точка 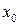 и уравнение прямой
и уравнение прямой  . Требуется: 1) составить уравнения касательной и нормали к данной кривой
. Требуется: 1) составить уравнения касательной и нормали к данной кривой 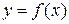 в точке с абсциссой
в точке с абсциссой 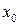 ; 2) найти точку на кривой
; 2) найти точку на кривой 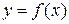 , в которой касательная параллельна прямой
, в которой касательная параллельна прямой  .
.
41. 


42. 

43. 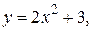

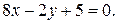
44. 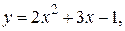


45. 
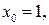

46. 

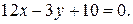
47. 
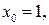

48. 


49. 
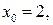

50. 
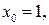

51–60. Найти производные  данных функций.
данных функций.
51. а)  , б)
, б) 

52. а)  , б)
, б)  .
.
53. а)  , б)
, б)  .
.
54. а)  , б)
, б)  .
.
55. а) 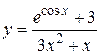 , б)
, б) 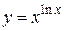 .
.
56. а)  , б)
, б)  .
.
57. а)  , б)
, б)  .
.
58. а) 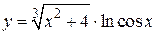 , б)
, б)  .
.
59. а)  , б)
, б)  .
.
60. а)  , б)
, б)  .
.
61–70. Вычислить пределы, используя правило Лопиталя.
61. а) 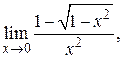 б)
б) 
62. а) 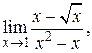 б)
б) 

63. а)  б)
б) 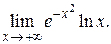
64. а)  б)
б) 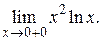

65. а)  б)
б) 
66. а) 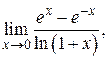 б)
б) 
67. а)  б)
б) 
68. а)  б)
б) 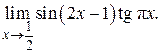
69. а)  б)
б) 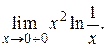
70. а)  б)
б) 
71–80. Исследовать функции с помощью производных первого и второго порядков. Найти асимптоты. Построить графики функций.
71. а)  , б)
, б)  . 72. а)
. 72. а)  , б)
, б)  .
.
73. а) 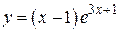 , б)
, б) 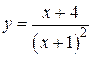 . 74. а)
. 74. а)  , б)
, б)  .
.
75. а) 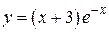 , б)
, б) 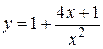 . 76. а)
. 76. а)  , б)
, б) 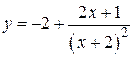 .
.
77. а)  , б)
, б)  . 78. а)
. 78. а) 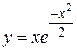 , б)
, б)  .
.
79. а) 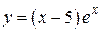 , б)
, б)  . 80. а)
. 80. а)  , б)
, б)  .
.
81–90. Найти неопределённые интегралы.
81. а)  , б)
, б)  , в)
, в) 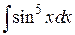 , г)
, г)  .
.
82. а)  , б)
, б) 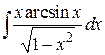 , в)
, в)  , г)
, г)  .
.
83. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
84. а)  , б)
, б)  , в)
, в)  , г)
, г) 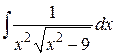 .
.
85. а)  , б)
, б) 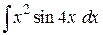 , в)
, в)  , г)
, г) 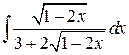 .
.
86. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
87. а)  , б)
, б) 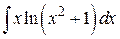 , в)
, в)  , г)
, г)  .
.
88. а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
89. а) 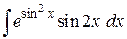 , б)
, б) 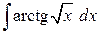 , в)
, в) 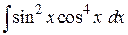 , г)
, г)  .
.
90. а)  , б)
, б) 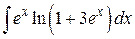 , в)
, в)  , г)
, г)  .
.
91–100. Вычислить несобственный интеграл или установить его расходимость.
91. 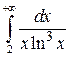 . 92.
. 92.  . 93.
. 93. 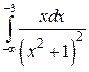 . 94.
. 94.  . 95.
. 95.  . 96.
. 96.  . 97.
. 97.  . 98.
. 98. 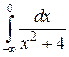 . 99.
. 99. 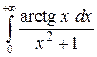 . 100.
. 100.  .
.
101–110. Найти общие решения дифференциальных уравнений.
101. а)  , б)
, б)  . 102. а)
. 102. а)  , б)
, б) 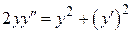 .
.
103. а) 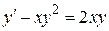 , б)
, б)  . 104. а)
. 104. а) 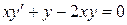 , б)
, б) 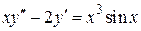 .
.
105. а) 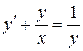 , б)
, б)  . 106. а)
. 106. а)  , б)
, б)  .
.
107. а)  , б)
, б)  . 108. а)
. 108. а)  , б)
, б)  .
.
109. а)  , б)
, б)  . 110. а)
. 110. а)  , б)
, б) 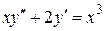 .
.
111–120. Найти общее решение неоднородного линейного дифференциального уравнения.
111. 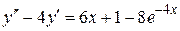 . 112.
. 112.  .
.
113.  . 114.
. 114. 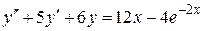 .
.
115.  . 116.
. 116. 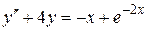 .
.
117. 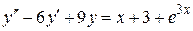 . 118.
. 118.  .
.
119.  . 120.
. 120.  .
.
121–130. Исследовать сходимость числового ряда.
121.  . 122.
. 122. 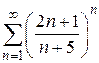 . 123.
. 123.  . 124.
. 124.  .
.
125.  . 126.
. 126.  . 127.
. 127. 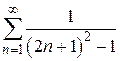 . 128.
. 128.  .
.
129.  . 130.
. 130. 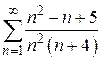 .
.
131–140. Найти область сходимости степенного ряда.
131.  . 132.
. 132.  . 133.
. 133.  . 134.
. 134.  .
.
135.  . 136.
. 136.  . 137.
. 137.  . 138.
. 138.  .
.
139.  . 140.
. 140. 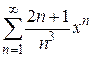
141–150. Вычислить определённый интеграл с точностью до 0,001, используя разложение подынтегральной функции в ряд Маклорена.
141.  . 142.
. 142.  . 143.
. 143. 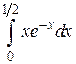 . 144.
. 144.  .
.
145.  . 146.
. 146.  . 147.
. 147.  . 148.
. 148.  .
.
149.  . 150.
. 150.  .
.
151–160. Найти точки экстремума функции  .
.
151. 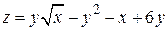 . 152.
. 152.  .
.
153.  . 154.
. 154. 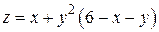 .
.
155.  . 156.
. 156.  .
.
157.  . 158.
. 158.  .
.
159.  . 160.
. 160.  .
.
161–170. Найти наименьшее m и наибольшее M значения функции  в замкнутой области D, заданной системой неравенств. Сделать чертёж
в замкнутой области D, заданной системой неравенств. Сделать чертёж
области D.
161. 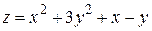 ,
,  .
.
162.  ,
,  .
.
163.  ,
,  .
.
164.  ,
,  .
.
165. 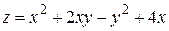 ,
,  .
.
166. 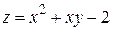 ,
,  .
.
167.  ,
,  .
.
168.  ,
,  .
.
169.  ,
,  .
.
170.  ,
,  .
.
171–180. Даны функция  , точка
, точка  и вектор
и вектор 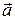 . Найти: 1) наибольшую скорость возрастания функции в точке А; 2) скорость изменения функции в точке А по направлению вектора
. Найти: 1) наибольшую скорость возрастания функции в точке А; 2) скорость изменения функции в точке А по направлению вектора 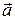 .
.
171. 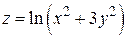 , А (1, 1),
, А (1, 1),  .
.
172.  , А (1, 1),
, А (1, 1),  .
.
173.  , А (2, 1),
, А (2, 1),  .
.
174.  , А (1, 1),
, А (1, 1),  .
.
175.  , А (-1, 2),
, А (-1, 2),  .
.
176. 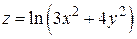 , А (1, 3),
, А (1, 3),  .
.
177.  , А (1, 2),
, А (1, 2),  .
.
178. 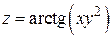 , А (2, 3),
, А (2, 3),  .
.
179. 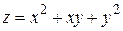 , А (1, 1),
, А (1, 1),  .
. 
180.  , А (2, 1),
, А (2, 1),  .
.
181–190. Задана пластина неравенствами в декартовой системе координат и  – плотностью материала, из которого изготовлена пластина. Найти массу пластины.
– плотностью материала, из которого изготовлена пластина. Найти массу пластины.
181.  ,
, 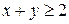 ;
;  . 182.
. 182.  ,
,  ;
; 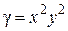 .
.
183.  ;
;  . 184.
. 184. 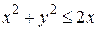 ,
,  ;
;  .
.
185.  ;
;  . 186.
. 186.  ,
,  ;
; 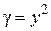 .
.
187.  ,
,  ;
;  . 188.
. 188.  ;
;  .
.
189.  ;
;  . 190.
. 190.  ;
;  .
.
191–200. Вычислить с помощью тройного интеграла объём тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на координатную плоскость ХОУ.
191.  . 192.
. 192. 
193.  . 194.
. 194.  .
.
195.  196.
196.  .
.
197.  . 198.
. 198. 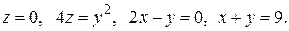
199. 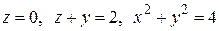 . 200.
. 200.  .
.
201–210. Найти поток векторного поля  через верхнюю сторону (в положительном направлении оси OZ) части плоскости Р, отсекаемой координатными плоскостями.
через верхнюю сторону (в положительном направлении оси OZ) части плоскости Р, отсекаемой координатными плоскостями.
201.  , Р:
, Р:  .
.
202.  , Р:
, Р:  .
.
203.  , Р:
, Р:  .
.
204.  , Р:
, Р: 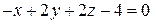 .
.
205.  , Р:
, Р:  .
.
206. 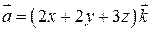 , Р:
, Р: 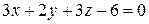 .
.
207. 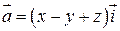 , Р:
, Р: 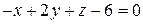 .
.
208. 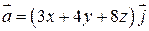 , Р:
, Р:  .
.
209.  , Р:
, Р:  .
.
210. 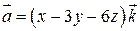 , Р:
, Р:  .
.
211–220. Найти поток векторного поля  : а) через внешнюю сторону замкнутой поверхности
: а) через внешнюю сторону замкнутой поверхности  , образованной поверхностью
, образованной поверхностью  и плоскостью Р; б) через верхнюю сторону (в положительном направлении оси OZ) части плоскости Р, вырезаемой поверхностью
и плоскостью Р; б) через верхнюю сторону (в положительном направлении оси OZ) части плоскости Р, вырезаемой поверхностью  ; в) через внешнюю сторону части поверхности
; в) через внешнюю сторону части поверхности  , отсекаемой плоскостью Р.
, отсекаемой плоскостью Р.
211. 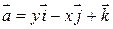 ,
,  :
:  , Р:
, Р:  .
.
212. 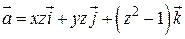 ,
,  :
:  , Р:
, Р:  .
.
213. 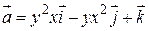 ,
,  :
:  , Р:
, Р:  .
.
214.  ,
,  :
:  , Р:
, Р:  .
.
215.  ,
,  :
:  , Р:
, Р:  .
.
216.  ,
,  :
: 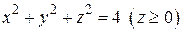 , Р:
, Р:  .
.
217.  ,
,  :
: 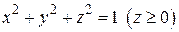 , Р:
, Р:  .
.
218. 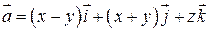 ,
,  :
: 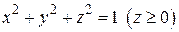 , Р:
, Р:  .
.
219.  ,
,  :
: 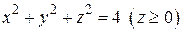 , Р:
, Р:  .
.
220. 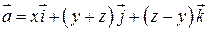 ,
,  :
:  , Р:
, Р:  .
.
221–230. Найти работу силы  при перемещении материальной точки
при перемещении материальной точки 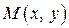 вдоль линии
вдоль линии  от точки А к точке В.
от точки А к точке В.
221.  , L: отрезок АВ,
, L: отрезок АВ,  ,
,  .
.
222. 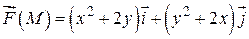 , L: отрезок АВ,
, L: отрезок АВ,  ,
,  .
.
223. 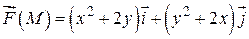 , L:
, L:  ,
,  ,
,  .
.
224.  , L:
, L:  ,
,  ,
,  .
.
225.  , L:
, L: 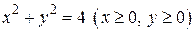 ,
,  ,
,  .
.
226.  , L:
, L:  ,
,  ,
,  .
.
227. 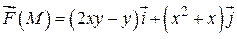 , L:
, L: 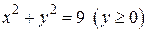 ,
,  ,
,  .
.
228.  , L:
, L:  ,
, 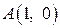 ,
, 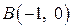 .
.
229. 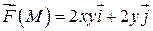 , L:
, L:  ,
, 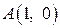 ,
,  .
.
230.  , L:
, L:  ,
,  ,
, 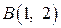 .
.
231–240. Проверить, является ли векторное поле  потенциальным и соленоидальным. В случае потенциальности поля
потенциальным и соленоидальным. В случае потенциальности поля  найти его потенциал.
найти его потенциал.
231.  .
.
232.  .
.
233.  .
.
234.  .
.
235.  .
.
236.  .
.
237. 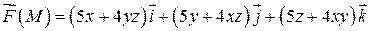 .
.
238.  .
.
239.  .
.
240.  .
.
241–250.
241. Три стрелка произвели по одному выстрелу по одной и той же мишени в одинаковых и независимых условиях. Вероятность поражения мишени первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что а) только один из стрелков попал в мишень; б) только два стрелка попали в мишень; в) все три стрелка попали в мишень.
242. В лотерее разыгрываются 10 билетов, из которых 5 выигрышных. Найти вероятность того, что среди 3 наудачу взятых билетов все оказались выигрышными.
243. В двух урнах находятся шары, отличающиеся только цветом. В первой урне – 5 белых, 11 чёрных и 8 красных шаров, во второй – соответственно 10, 8 и 6. Из каждой урны извлекают по одному шару. Найти вероятность того, что оба шара окажутся одного цвета.
244. В коробке 5 изделий, из которых 3 бракованные. Наудачу извлекаются
2 изделия. Найти вероятность того, что среди них окажется хотя бы одно бракованное изделие.
245. Студент знает ответы на 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что студент, взявший экзаменационный билет ответит: а)на все три вопроса; б) на два вопроса из трёх; в) только на один вопрос экзаменационного билета.
246. Для производственной практики 20 студентам предоставлено 15 мест в Екатеринбурге и 5 – в Челябинске. Найти вероятность того, что два определённых студента попадут на практику в один город.
247. Два стрелка произвели по одному выстрелу по одной и той же мишени в одинаковых и независимых условиях. Вероятность поражения мишени первым стрелком равна 0,7, вторым – 0,8. Найти вероятность того, что а) мишень поражена; б) мишень поражена только одним из стрелков; в) мишень поражена дважды.
248. Экспедиция отправила газеты в два почтовых отделения. Вероятность своевременной доставки газет в каждое отделение равна 0,9. Найти вероятность того, что а) оба почтовых отделения получат газеты вовремя; б) только одно почтовое отделение получит газеты вовремя; в) хотя бы одно почтовое отделение получит газеты вовремя.
249. На 12 человек выделили путёвки в 4 дома отдыха: 3 путёвки в первый дом отдыха, 3 – во второй, 2 – в третий и 4 – в четвёртый. Найти вероятность того, что 3 определённых человека поедут в один дом отдыха.
250. Для аварийной сигнализации установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0, 95, третье – 0,85. Найти вероятность того, что при аварии сработает а) только одно устройство; б) только два устройства; в) все три устройства.
251–260. Вероятность наступления события А в каждом из независимых испытаний равна р. Найти вероятность того, что событие А наступит к раз в n испытаниях.
251. а)  б)
б) 
252. а)  б)
б) 
253. а) 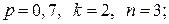 б)
б) 
254. а)  б)
б) 
255. а)  б)
б) 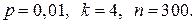
256. а)  б)
б) 
257. а)  б)
б) 
258. а)  б)
б) 
259. а) 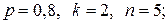 б)
б) 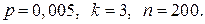
260. а) 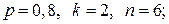 б)
б) 
261–270. Известны математическое ожидание а и среднее квадратическое отклонение  нормально распределённой случайной величины Х. Найти плотность вероятности и функцию распределения этой случайной величины. Найти вероятность попадания её на отрезок
нормально распределённой случайной величины Х. Найти плотность вероятности и функцию распределения этой случайной величины. Найти вероятность попадания её на отрезок  .
.
261. 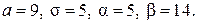 262.
262. 
263.  264.
264. 
265. 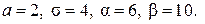 266.
266. 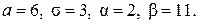
267.  268.
268. 
269.  270.
270. 
271–280. Из генеральной совокупности, распределённой по нормальному закону, взята выборка. Найти: а) выборочную среднюю 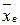 ; б) выборочное среднее квадратическое отклонение
; б) выборочное среднее квадратическое отклонение  ; в) с надёжностью
; в) с надёжностью 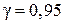 доверительный интервал для оценки математического ожидания а генеральной совокупности при известной дисперсии
доверительный интервал для оценки математического ожидания а генеральной совокупности при известной дисперсии  .
.
271.
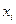
| 10,6 | 15,6 | 20,6 | 25,6 | 30,6 | 35,6 | 40,6 |

|
272.
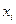
| |||||||

|
273.
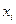
| |||||||

|
274.
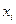
| |||||||

|
275.
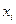
| 12,4 | 16,4 | 20,4 | 24,4 | 28,4 | 32,4 | 36,4 |

|
276.
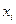
| |||||||

|
277.
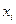
| |||||||

|
278.
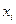
| |||||||

|
279.
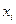
| 12,5 | 13,0 | 13,5 | 14,0 | 14,5 | 15,0 | 15,5 |

|
280.
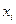
| 10,2 | 10,9 | 11,6 | 12,3 | 13,0 | 13,7 | 14,4 |

|
281–290. Из системы векторов выделить максимальную линейно независимую подсистему векторов, и остальные векторы выразить через них.
281.  ,
, 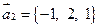 ,
,  ,
,  .
.
282.  ,
,  ,
,  ,
,  .
.
283.  ,
,  ,
,  ,
,  .
.
284. 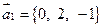 ,
,  ,
, 
 .
.
285.  ,
,  ,
,  ,
,  .
.
286. 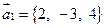 ,
, 
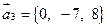 ,
,  .
.
287.  ,
, 
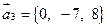 ,
,  .
.
288. 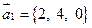 ,
,  ,
,  ,
,  .
.
289.  ,
, 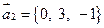 ,
,  ,
, 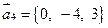 .
.
290. 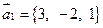 ,
,  ,
, 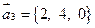 ,
,  .
.
291–300. Даны матрицы А, В и  . Решить систему
. Решить систему  :
:
а) методом Гаусса; б) по формулам Крамера.
291.  292.
292. 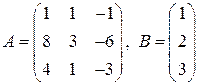
293.  294.
294. 
295. 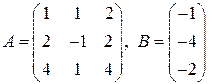 296.
296. 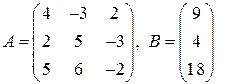
297.  298.
298. 
299.  300.
300. 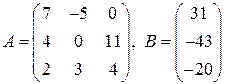
301–310. Найти собственные значения и собственные вектора линейного оператора, заданного в некотором базисе матрицей А.
Не нашли, что искали? Воспользуйтесь поиском: