
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
2 страница. 1. Знайти область визначення функції .
№ 5
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б) 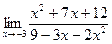 ;
;
в)  ;г)
;г)  ; д)
; д) 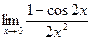 .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 6
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 7
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 8
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 9
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 10
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б) 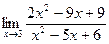 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 11
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б) 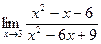 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 12
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 13
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 14
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 15
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  г)
г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 16
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 17
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б) 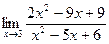 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 18
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в) 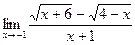 ; г)
; г)  ; д)
; д) 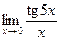 .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 19
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 20
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ;г)
;г)  ;
;
д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 21
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в) 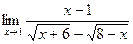 ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 22
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 23
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  г)
г) 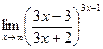 ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 24
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 25
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 26
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 27
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 28
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 29
1. Знайти область визначення функції  .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

№ 30
1. Знайти область визначення функції 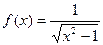 .
.
2. Знайти границі функцій:
a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
3. Дослідити функцію на неперервність і побудувати її графік:

Cамостійна робота № 3. Похідна та її застосування
№1
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б)  в)
в) 
г)  д)
д) 
2. Обчислити наближено  .
.
3. Із дроту довжиною  виготовляють модель прямокутного паралелепіпеда з квадратною основою. Якою повинна бути довжина сторони основи, щоб повна поверхня паралелепіпеда була найбільшою?
виготовляють модель прямокутного паралелепіпеда з квадратною основою. Якою повинна бути довжина сторони основи, щоб повна поверхня паралелепіпеда була найбільшою?
№ 2
1. Користуючись правилами диференціювання, знайти похідні
y'x заданих функцій:
а)  б)
б)  в)
в) 
г)  д)
д) 
2. Знайти рівняння дотичної і нормалі до кривої  в точці з абсцисою
в точці з абсцисою 

3. Знайти найбільший об’єм конуса при заданій довжині  його твірної.
його твірної.
№ 3
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
в)  г)
г)  д)
д) 
2. Обчислити наближено 
3. Периметр осьового перерізу циліндра дорівнює 6а. Знайти найбільший об’єм такого циліндра.
№ 4
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
в)  г)
г)  д)
д) 
2. Знайти рівняння дотичної і нормалі до кривої  в точці з абсцисою
в точці з абсцисою 

3. Знайти прямокутний трикутник найбільшої площі, гіпотенуза якого дорівнює с.
№ 5
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
в)  г)
г)  д)
д) 
2. Обчислити наближено 
3. Розкласти число 20 на два доданки так, щоб їх добуток був найбільшим.
№ 6
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а) 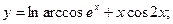 б)
б)  в)
в) 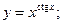
в) 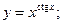 г)
г)  д)
д) 
2. Знайти рівняння дотичної і нормалі до кривої  в точці абсцисою
в точці абсцисою 

3. Сіткою довжиною 120м потрібно огородити прилеглу до будинку прямокутну ділянку найбільшої площі. Визначити розміри цієї ділянки.
№ 7
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
в)  г)
г)  д)
д) 
2. Обчислити наближено 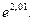
3. Довести, що з усіх прямокутників, вписаних у заданий круг, найбільшу площу має квадрат.
№ 8
1.Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
в)  г)
г)  д)
д) 
2. Знайти рівняння дотичної і нормалі до кривої  в точці з абсцисою
в точці з абсцисою 

3. Показати, що з усіх рівнобедрених трикутників, вписаних у заданий круг, найбільший периметр має рівносторонній трикутник.
№ 9
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а) 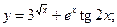 б)
б) 
в)  г)
г)  д)
д) 
2. Обчислити наближено 
3. Внутрішня поверхня баку із квадратною основою без кришки рівна 108 дм3. Якими повинні бути розміри баку, щоб його об’єм був найбільшим?
№ 10
1.Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
в)  г)
г)  д)
д) 
2. Знайти рівняння дотичної і нормалі до кривої  в точці
в точці 
3. Показати, що з усіх трикутників із заданою основою та заданим кутом при протилежній вершині, найбільший периметр буде мати рівнобедрений трикутник.
№ 11
1. Користуючись правилами диференціювання, знайти похідні y'x заданих функцій:
а)  б)
б) 
Не нашли, что искали? Воспользуйтесь поиском: