
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
5 страница. 2. Обчислити невласні інтеграли або довести їх розбіжність:
y = x2+ 4 x, y = x+ 4.
№ 28
1. Знайти інтеграли:
а)  б)
б)  в)
в) 
2. Обчислити невласні інтеграли або довести їх розбіжність:
а)  б)
б) 
3. Обчислити площу фігури, обмеженої лініями
y = x2, y2 = x.
№ 29
1. Знайти інтеграли:
а)  б)
б)  в)
в) 
2. Обчислити невласні інтеграли або довести їх розбіжність:
а)  б)
б) 
3. Обчислити площу фігури, обмеженої лініями
y = 
 .
.
№ 30
1. Знайти інтеграли:
а)  б)
б)  в)
в) 
2. Обчислити невласні інтеграли або довести їх розбіжність:
а) 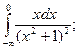 б)
б) 
3. Обчислити площу фігури, обмеженої лініями
y= 3 - 2 x, 
Cамостійна робота №6. Звичайні диференціальні рівняння
Проінтегрувати диференціальні рівняння:
№ 1
1.  2.
2. 
3.  4.
4. 
5. 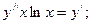 6.
6. 
№ 2
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 3
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 4
1.  2.
2. 
3.  4.
4. 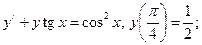
5.  6.
6. 
№ 5
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 6
1.  2.
2. 
3.  4.
4. 
5. 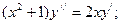 6.
6. 
№ 7
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 8
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 9
1.  2.
2. 
3. 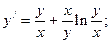 4.
4. 
5.  6.
6. 
№ 10
1.  2.
2. 
3.  4.
4. 
5. 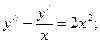 6.
6. 
№ 11
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 12
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 13
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 14
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 15
1. 
2.  3.
3. 
4.  5.
5. 
6. 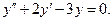
№ 16
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 17
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 18
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 19
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 20
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 21
1.  2.
2. 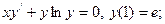
3.  4.
4. 
5.  6.
6. 
№ 22
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 23
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 24
1. 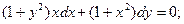 2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 25
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 26
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 27
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 28
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
№ 29
1.  2.
2. 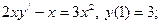
3.  4.
4. 
5.  6.
6. 
№ 30
1.  2.
2. 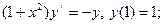
3.  4.
4. 
5. 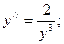 6.
6. 
Відповіді до окремих завдань
Частина1
1.1
1. а)  б)
б)  в) несумісна;
в) несумісна;
г)  д) несумісна;
д) несумісна;
е) 
2. а) 10; б) -56; в) 10,5; г) 
3.а)  =(-1;2;1),
=(-1;2;1),  ;
; 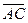 =(0;1;-2),
=(0;1;-2),  б)
б)  ;
;
в)  . 4. α = -3.
. 4. α = -3.
5.а) АВ: 
АС:  б)
б) 
в)  г)
г) 
 (лін.од.);
(лін.од.);
д)  е) 1.
е) 1.  2.
2.  є)
є)  .
.
6.  . 7.
. 7.  .
.
8. а =3, b =2, F 1(0;-  ),
),  (0;
(0;  ), ε=
), ε=  . 9.
. 9.  .
.
10. F 1(-5;0), F 2(5;0), ε= 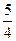 , y=±
, y=±  x. 11. (2;1), (-6;9).
x. 11. (2;1), (-6;9).
12. а)  – коло;
– коло;
б)  – еліпс; в)
– еліпс; в)  – гіпербола; г)
– гіпербола; г)  – парабола.
– парабола.
1.2
1. а)  ; б)
; б) 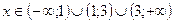 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
2. а)  ; б) 0; в) ∞; г)
; б) 0; в) ∞; г)  ; д)
; д)  ; е)
; е)  ; є)
; є)  ; ж)
; ж)  ; з)
; з)  .
.
3. х= 1 – точка розриву І-го роду.
1.3
1. а)  ;
;
б)  ;
;
в)  ; г) -1;
; г) -1;
д)  .
.
2. а) -0,1; б) 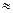 1,994. 3. х+у- 4 =0; х-у= 0. 4.
1,994. 3. х+у- 4 =0; х-у= 0. 4.  .
.
1.4
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ; 5.
; 5.  ;
;
6.  ; 7.
; 7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  ; 13.
; 13.  ;
;
14. 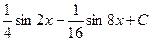 ; 15.
; 15.  ; 16.
; 16.  .
.
1.5
1. а) 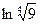 ; б)
; б)  ; в)
; в)  . 2. а) π; б) розбіжний.
. 2. а) π; б) розбіжний.
3. а) 4,5 кв.од.; б) 12 кв.од.
1.6
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
11. 
Використана та рекомендована література
1. Антонюк Р.А. Вища математика. Навчальний посібник. – Рівне: НУВГП, 2005. – 246 с.
2. Антонюк Р.А. Вища математика. Інтерактивний комплекс навчально-методичного забезпечення. – Рівне: НУВГП, 2007. – 70 с.
3. Бараненков Г.С. и др. Задачи и упражнения по математическому анализу / Под ред. Демидовича Б.П. – М.: Наука, 1972. – 480 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 1,2. – М.: Высшая школа, 1986.
5. Каплан И.А. Практические занятия по высшей математике. Ч.1-3. – Харьков, ХГУ, 1972.- 946 с.
6. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. – 240 с.
7. Лубенська Т.В., Чупаха Л.Д. Вища математика в таблицях: Довідник. – К.: МАУП, 1999. – 88 с.
8. Пискунов Н.С. Дифференциальное и интегральное исчисление. – Т. 1,2. – М.: Наука, 1987.
Не нашли, что искали? Воспользуйтесь поиском: