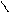ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ферма, Ролль, Лагранж теоремалары 1 страница
Ферма теоремасы. х0 нүктесі y=f(x) функциясының экстремум нүктесі болып ж-е осы нүктедегі f’(x0)функция туындысы бар болса, онда f’(x)=0. Бұл теореманың геометриялық мағынасы: теорема шартын қанағаттандыратын нүктеде функция графигіне жүргізілген жанама абсцисса осіне параллель болады.
Лагранж теоремасы. Егер (x0,y0) нүкте z=f(x,y) функциясының g(x,y)=0 шартын қанағаттандыратын шартты экстремум нүктесі болса, онда қандай да бір λ0 табылады да,(x0,y0,z0) нүкте L (x,y,λ) функциясының экстремум нүктесі болады.
Ролль теоремасы — дифференциалдық есептеудің негізгі теоремаларының бірі. Егер f(x) функциясы axb аралығында үзіліссіз болып, осы аралықтың әрбір ішкі нүктесінде дифференциалданса және шеткі нүктелеріндегі мәндері тең болса, яғни f(a)=f(b), онда (a, b) интервалында f¢(x) функциясы нөлге айналатын кем дегенде бір с нүктесі болады: a<c<b; f¢(с)=0. Ролль теоремасын алғаш рет 1690 ж. француз математигі М.Ролль (1652 — 1719) алгебралық көпмүшеліктер үшін тұжырымдаған
28. Туындының экономикалық қолданыстары. Функция иілгіштігі
Айталық y=f(x) функциясы өндірілген өнім х көлемінен оған кеткен у шығын арасындағы байланысты сипаттасын.
Егер өндіріс көлемін х -тен  -ке арттырсақ, яғни
-ке арттырсақ, яғни  бірлікке, онда жұмсалған шығын да
бірлікке, онда жұмсалған шығын да  бірлікке көбейеді.
бірлікке көбейеді.
Ал  қатынас өндіріс көлемін
қатынас өндіріс көлемін  бірлікке өзгерткендегі орташа шығынды береді.
бірлікке өзгерткендегі орташа шығынды береді.  жағдайдағы
жағдайдағы  қатынастың шегі, яғни
қатынастың шегі, яғни 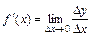 , өндірістің шектік шығынын береді.
, өндірістің шектік шығынын береді.
 шаманы аз деп есептесек
шаманы аз деп есептесек 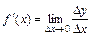 формуланы мынадай түрде жазуға болады:
формуланы мынадай түрде жазуға болады:
 ,осыдан
,осыдан  немесе
немесе  .
.
Егер х өте үлкен шама деп, ал  шаманы аз деп, айталық
шаманы аз деп, айталық  деп есептесек, онда
деп есептесек, онда  немесе
немесе  . Сонымен, өндірістің шектік шығыны өндіріс көлемін
. Сонымен, өндірістің шектік шығыны өндіріс көлемін  бірлікке өзгерткендегі үстеме өнім өндіруге кеткен қосымша шығынға тең болады.
бірлікке өзгерткендегі үстеме өнім өндіруге кеткен қосымша шығынға тең болады.
Мысалы, y=f(x) функциясы қандай да бір уақыт мезетінде х жұмысшының у өндірілген өнім көлемі арасындағы байланысты сипаттасын. Айталық, фирма тағы бір адамды жұмысқа қабылдады. Онда 
шама жаңадан келген жұмысшының өндірген өнім көлемі.
Егер С- өнім бірлігі (бағасы), ал р – фирманың жұмысшыға уақыт мезетінде төлейтін жалақысы болса, онда  болған кезде фирмаға тағы бір жұмысшыны алуға болады, себебі жұмысшының фирмаға түсіретін пайдасы одан алатын жалақысынан көп. Осы ара қатынасты экономиканың алтын заңы дейді.
болған кезде фирмаға тағы бір жұмысшыны алуға болады, себебі жұмысшының фирмаға түсіретін пайдасы одан алатын жалақысынан көп. Осы ара қатынасты экономиканың алтын заңы дейді.
y=f(x) функциясы қандай да бір уақыт мезетінде у өндірілген өнім көлемінің х адам еңбегінен тәуелділігін сипаттаса, онда  шаманы х нүктесіндегі шектік еңбек өнімділігі деуге болады.
шаманы х нүктесіндегі шектік еңбек өнімділігі деуге болады.
Функция иілгіштігі. y=f(x) функциясы у шаманың х шамадан тәуелділігін білдірсін. Тәуелсіз аргумент 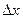 шамаға өзгергенде тәуелді айнымалы да
шамаға өзгергенде тәуелді айнымалы да  шамаға өзгереді. Мынадай сұрақ туындайды, у тәуелді айнымалының х аргумент өзгерісіне деген иілгіштігін қалай өлшеу керек. Бір айнымалының екінші айнымалыға әсерін сипаттайтын шама ретінде туындыны алуға болады. Ол функцияның аргумент өзгерісіне қатысты өзгеріс жылдамдығын сипаттайды. Бірақ экономикада бұл қолайсыздау, себебі ол шамаларды немен өлшейтінімізге байланысты. Мысалы, қандай да бір затқа деген q сұраныс функциясының оның p бағасынан тәуелділігін алсақ, онда туынды
шамаға өзгереді. Мынадай сұрақ туындайды, у тәуелді айнымалының х аргумент өзгерісіне деген иілгіштігін қалай өлшеу керек. Бір айнымалының екінші айнымалыға әсерін сипаттайтын шама ретінде туындыны алуға болады. Ол функцияның аргумент өзгерісіне қатысты өзгеріс жылдамдығын сипаттайды. Бірақ экономикада бұл қолайсыздау, себебі ол шамаларды немен өлшейтінімізге байланысты. Мысалы, қандай да бір затқа деген q сұраныс функциясының оның p бағасынан тәуелділігін алсақ, онда туынды  мәні (баға теңгемен өлшенгенде) сұраныс немен өлшенетіндігіне байланысты. Егер кг өлшенсе, туынды кг/тг, ал центенермен өлшенсе ц/тг болады. Баға бірдей болғанымен, туынды мәндері әртүрлі. Сондықтан экономикада бір айнымалының екінші айнымалы өзгерісіне деген сезімталдығын өрнектейтін өлшем бірліксіз шама енгізіледі. Ондай шама ретінде айнымалылардың абсолюттік өзгерістерінің
мәні (баға теңгемен өлшенгенде) сұраныс немен өлшенетіндігіне байланысты. Егер кг өлшенсе, туынды кг/тг, ал центенермен өлшенсе ц/тг болады. Баға бірдей болғанымен, туынды мәндері әртүрлі. Сондықтан экономикада бір айнымалының екінші айнымалы өзгерісіне деген сезімталдығын өрнектейтін өлшем бірліксіз шама енгізіледі. Ондай шама ретінде айнымалылардың абсолюттік өзгерістерінің  қатынасы емес, олардың салыстырмалы немесе проценттік өзгерістерінің қатынасын алады, яғни
қатынасы емес, олардың салыстырмалы немесе проценттік өзгерістерінің қатынасын алады, яғни
29.Функцияның экстремумның қажетті және жеткілікті шарты. х0 нүктесінің  - маңайы табылып, (х0-
- маңайы табылып, (х0-  х0+
х0+  ), осы маңайдағы барлық х
), осы маңайдағы барлық х  х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясының максимум нүктесі деп аталады. Функцияның минимум және максимум нүктелерін экстремум нүктелері деп атайды. Осы нүктелердегі функция мәндерін функция экстремумдары дейді. Ферма теоремасы. х0 нүктесі y=f(x) функциясының экстремум нүктесі болып және осы нүктедегі
х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясының максимум нүктесі деп аталады. Функцияның минимум және максимум нүктелерін экстремум нүктелері деп атайды. Осы нүктелердегі функция мәндерін функция экстремумдары дейді. Ферма теоремасы. х0 нүктесі y=f(x) функциясының экстремум нүктесі болып және осы нүктедегі  функция туындысы бар болса, онда
функция туындысы бар болса, онда  =0. Экстремумның бірінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір
=0. Экстремумның бірінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір  - маңайында функция туындысы бар болсын (х0 нүктесінде туынды болмауы мүмкін). Онда,1)егер х аргумент х0 нүкте арқылы өткенде
- маңайында функция туындысы бар болсын (х0 нүктесінде туынды болмауы мүмкін). Онда,1)егер х аргумент х0 нүкте арқылы өткенде  таңбасын оңнан теріске өзгертсе, онда х0 нүкте максимум нүктесі болады;2)егер х аргумент х0 нүкте арқылы өткенде
таңбасын оңнан теріске өзгертсе, онда х0 нүкте максимум нүктесі болады;2)егер х аргумент х0 нүкте арқылы өткенде  таңбасын терістен оңға өзгертсе, онда х0 нүкте минимум нүктесі болады; 3)егер х аргумент х0 нүкте арқылы өткенде
таңбасын терістен оңға өзгертсе, онда х0 нүкте минимум нүктесі болады; 3)егер х аргумент х0 нүкте арқылы өткенде  таңбасын өзгертпесе, онда х0 нүкте экстремум нүктесі емес. Экстремумның екінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір
таңбасын өзгертпесе, онда х0 нүкте экстремум нүктесі емес. Экстремумның екінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір  - маңайында екі рет дифференциалдансын. Сонымен қатар
- маңайында екі рет дифференциалдансын. Сонымен қатар 
 болса, онда 1)егер
болса, онда 1)егер  болса, онда х0 нүкте f(x) функциясының максимум нүктесі болады;2)егер
болса, онда х0 нүкте f(x) функциясының максимум нүктесі болады;2)егер  болса, онда х0 нүкте f(x) функциясының минимум нүктесі болады.
болса, онда х0 нүкте f(x) функциясының минимум нүктесі болады.
30. Функция графигінің дөңестегі, ойыстығы және иілу нүктелері. y=f(x) функция графигі (а,в) интервалының кез келген нүктесінде жүргізілген жанамадан төмен жатса, онда функция дөңес (дөңестігі жоғары қараған) деп, ал жанамадан жоғары жатса, онда функция ойыс (дөңестігі төмен қараған) деп аталады. атайды.Функция графигінің дөңес және ойыс бөліктерін бөліп тұратын нүктені функцияның иілу нүктесі деп атайды. Функция дөңестігінің жеткілікті шарты. (а,в) интервалында y=f(x) функциясының екінші ретті туындысы теріс таңбалы болса, функция графигі осы аралықта дөңес, ал екінші туындысы оң таңбалы болса, функция графигі осы аралықта ойыс болады. Иілу нүктесі бар болуының қажетті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының (x0, f(x0)) нүктесі иілу нүктесі болса, онда 
31. Асимптота. Фун-ны зерттеп, график салудың жалпы сүлбесі. Анықтама. Егер y=f(x) функциясы үшін  және
және  шектерінің ең болмағанда біреуі шексіздікке тең болса, онда
шектерінің ең болмағанда біреуі шексіздікке тең болса, онда  функция графигінің тік асимптотасы деп аталады (6а-сурет).у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса (6б-сурет).
функция графигінің тік асимптотасы деп аталады (6а-сурет).у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса (6б-сурет).


|
Көлбеу асимптотаның дербес жағдайы
(k=0) горизонталь асимптота болады: y=b Көлбеу асимптотаны мынадай теорема көмегімен табуға болады. Теорема. у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы болуы үшін мынадай шектердің бар болуы қажетті және жеткілікті:  ,
,  . Функцияны зерттеп оның графигін салуды мынадай ретпен жүргізген жөн:
. Функцияны зерттеп оның графигін салуды мынадай ретпен жүргізген жөн:
1. Функцияның анықталу облысын табу;
2. функцияны жұп, тақтылыққа зерттеу;
3. функцияны периодтылыққа зерттеу;
4. функцияны үзіліссіздікке зерттеп, үзіліс нүктелерін табу;
5. күдікті нүктелерін табу;
6. монотонды аралығы мен экстремумдарын табу;
7. ойыс, дөңес аралықтарын, иілу нүктелерін табу;
8. функция графигінің асимптоталарын табу;
9. функция графигінің координаталар осімен қилысу нүктелерін;
10. зерттеулерге сүйеніп график салу.
32. Интеграл қасиеттері. Интегралдар кестесі.
. f(x) және F(x) функциялары ақырлы немесе ақырсыз Х аралықта анықталған функциялар болсын. Анықтама. Х аралығында дифференциалданатын  функциясы теңдігін қанағаттандырса,
функциясы теңдігін қанағаттандырса,  функциясы f(х) функциясының алғашқы функциясы деп аталады Берілген функцияның алғашқы функциясын табу амалы функцияны интегралдау деп аталады. Функцияны интегралдау амалы дифференциалдау амалына кері амал. Интеграл анықтамасынан мынадай қасиеттер шығады.
функциясы f(х) функциясының алғашқы функциясы деп аталады Берілген функцияның алғашқы функциясын табу амалы функцияны интегралдау деп аталады. Функцияны интегралдау амалы дифференциалдау амалына кері амал. Интеграл анықтамасынан мынадай қасиеттер шығады.
1.  .
.
2.  .
.
3.  = F(x) + C.
= F(x) + C.
4. Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x) + g(x) функциясының да алғашқы функциясы бар болады және 

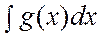
5. 
 .
.
6. Егер  = F(x) + C болса, онда
= F(x) + C болса, онда  =
= 
F(ax+b) + C
7. Егер интеграл астындағы функцияның алымы бөлімнің туындысы болса, онда интеграл бөлімнің абсолют шамасының наткрал логарифміне тең, яғни  , мұндағы u=u(x).
, мұндағы u=u(x).
ИНТЕГРАЛДАР КЕСТЕСІ
 = C
= C  = x + C
= x + C  =
= 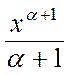 + C, x>0,
+ C, x>0, 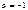
 = ln| x |+ C, x
= ln| x |+ C, x  0
0  =
=  + C,
+ C, 
 =
=  + C
+ C 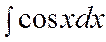 = sinx + C
= sinx + C
 =- cosx + C
=- cosx + C 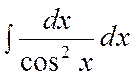 = tgx + C,
= tgx + C, 
 =- ctgx + C,
=- ctgx + C, 
 = arcsinx + C, -1<x<1
= arcsinx + C, -1<x<1  = arctgx + C
= arctgx + C  =
= 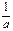 artg
artg  + C
+ C
 =
= 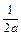 ln
ln  + C
+ C  ln
ln  +C
+C
33. Айнымалыларды алмастыру және бөліктеп интегралдау әдісі.
I=  интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және
интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және 
 . Бұләдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интегралды бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Мысалдар қарастырайық.
. Бұләдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интегралды бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Мысалдар қарастырайық.


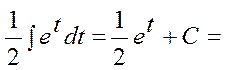
 +С
+С 

 arctgt+C= =
arctgt+C= = 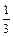 arctgx3+C
arctgx3+C
В 

 ln|t|+C=ln|1+lnx|+с. Бөліктеп интегралдау әдісі. Бұл әдіс мынадай қатынасқа негізделген: d(uv) = udv + vdu
ln|t|+C=ln|1+lnx|+с. Бөліктеп интегралдау әдісі. Бұл әдіс мынадай қатынасқа негізделген: d(uv) = udv + vdu 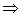 udv = d(uv) – vdu
udv = d(uv) – vdu
мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ,  , осыдан
, осыдан 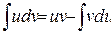 .Бұл әдісті қолданғанда u және v функцияларын
.Бұл әдісті қолданғанда u және v функцияларын  интеграл
интеграл 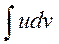 интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық. а)
интегралға қарағанда оңай алынатындай етіп таңдайды. Мысалдар қарастырайық. а) 

 +С =
+С =  +C.б)
+C.б) 




 . J=
. J=  (cosx+sinx)-J
(cosx+sinx)-J 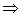 J=
J= 
 (cosx+sinx)+C. Төмендегі интегралдар тобы тек бөліктеп интегралдау әдісімен есептелінеді:
(cosx+sinx)+C. Төмендегі интегралдар тобы тек бөліктеп интегралдау әдісімен есептелінеді:  ;
;  ;
;  ;
;  .
.
34. Қарапайым рационал функцияларды интегралдау
 түріндегі өрнекті n– дәрежелі көпмүшелік деп атайды. Мұндағы
түріндегі өрнекті n– дәрежелі көпмүшелік деп атайды. Мұндағы  - нақты сандар (
- нақты сандар ( , n >0). Көпмүшеліктердің қатынасы түрінде берілген өрнек рационал өрнек болады. Мысалы
, n >0). Көпмүшеліктердің қатынасы түрінде берілген өрнек рационал өрнек болады. Мысалы  , бөлшектер раци
, бөлшектер раци  онал өрнектер. Егер бөлшектің алымындағы көпмүшеліктің дәрежесі бөліміндегі көпмүшелік дәрежесінен кем болса, бөлшек дұрыс деп, ал кем болмаса бөлшек бұрыс деп аталады. Мысалдағы біріншісі бөлшек - дұрыс, ал екіншісі – бұрыс бөлшек. Кез келген бұрыс бөлшекті алымын бөлімге бөлу арқылы дұрыс бөлшекке келтіріп алуға болады. Мысалы,
онал өрнектер. Егер бөлшектің алымындағы көпмүшеліктің дәрежесі бөліміндегі көпмүшелік дәрежесінен кем болса, бөлшек дұрыс деп, ал кем болмаса бөлшек бұрыс деп аталады. Мысалдағы біріншісі бөлшек - дұрыс, ал екіншісі – бұрыс бөлшек. Кез келген бұрыс бөлшекті алымын бөлімге бөлу арқылы дұрыс бөлшекке келтіріп алуға болады. Мысалы,  бөлшекті дұрыс бөлшекке келтірейік:
бөлшекті дұрыс бөлшекке келтірейік:  Сонымен, берілген бөлшектің бүтін бөлігін бөліп дұрыс бөлшекке келтірдік:
Сонымен, берілген бөлшектің бүтін бөлігін бөліп дұрыс бөлшекке келтірдік:  .Мектеп курсынан көпмүшеліктің мынадай қасиеті белгілі: Кез келген көпмүшелікті
.Мектеп курсынан көпмүшеліктің мынадай қасиеті белгілі: Кез келген көпмүшелікті  және
және  түріндегі көбейткіштерге жіктеуге болады. Мынадай тұжырым дұрыс болады: Егер дұрыс рационал бөлшек бөлімі
түріндегі көбейткіштерге жіктеуге болады. Мынадай тұжырым дұрыс болады: Егер дұрыс рационал бөлшек бөлімі  және
және  түріндегі көбейткіштерге жіктелген болса, онда бөлшектімынадай қарапайым бөлшектердің қосындысына жіктеуге болады:
түріндегі көбейткіштерге жіктелген болса, онда бөлшектімынадай қарапайым бөлшектердің қосындысына жіктеуге болады: 

 , мұндағы, Р(х) – белгілі көпмүшелік,
, мұндағы, Р(х) – белгілі көпмүшелік, 
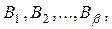
 - белгісіз коэффициенттер. Ол коэффициенттерді табу үшін белгісіз коэффициенттер әдісін пайдаланамыз: теңдіктің оң жағын ортақ бөлімге келтіреміз; екі бөлшектің бөлімдері тең болатындықтан, алымдарын теңестіреміз; теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз; осы жүйені шешіп белгісіз коэффициенттерді табамыз. Мысалы
- белгісіз коэффициенттер. Ол коэффициенттерді табу үшін белгісіз коэффициенттер әдісін пайдаланамыз: теңдіктің оң жағын ортақ бөлімге келтіреміз; екі бөлшектің бөлімдері тең болатындықтан, алымдарын теңестіреміз; теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз; осы жүйені шешіп белгісіз коэффициенттерді табамыз. Мысалы  бөлшегін қарапайым бөлшектер қосындысына жіктейік Бөлшек дұрыс, сондықтан (2) формула бойынша бөлшекті жіктейміз,
бөлшегін қарапайым бөлшектер қосындысына жіктейік Бөлшек дұрыс, сондықтан (2) формула бойынша бөлшекті жіктейміз,  Белгісіз коэффициенттерді табу үшін теңдіктің оң жағын ортақ бөлімге келтіріп жазайық:
Белгісіз коэффициенттерді табу үшін теңдіктің оң жағын ортақ бөлімге келтіріп жазайық:  .Теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз:
.Теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз:  Төрт белгісізді, төрт теңдеуден тұрған жүйені шешіп, белгісіз коэффициенттерді табамыз:
Төрт белгісізді, төрт теңдеуден тұрған жүйені шешіп, белгісіз коэффициенттерді табамыз:  .Табылған мәндерді теңдіктегі орнына қойып, бөлшектің қарапайым жіктелуін аламыз:
.Табылған мәндерді теңдіктегі орнына қойып, бөлшектің қарапайым жіктелуін аламыз:  . Енді осы рационал бөлшекті интегралдайық.
. Енді осы рационал бөлшекті интегралдайық. 
 Әр интегралды жеке қарастырайық. 1)
Әр интегралды жеке қарастырайық. 1) 
 , мұнда бөлшектің алымы бөлімінің туындысы болғандықтан 7-қасиетті пайдаландық. 2)
, мұнда бөлшектің алымы бөлімінің туындысы болғандықтан 7-қасиетті пайдаландық. 2) 

 + С=
+ С=  +C=
+C=  +C; 3)
+C; 3) 


 +4=
+4=  +
+ 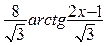 +C, мұнда бірінші қосылғышты алымы бөлімінің туындысы болғандай етіп түрлендірдік те 7-қасиетті пайдаландық. Ал екінші қосылғышта бөлімінің толық квадратын бөліп алып, интегралдар кестесіндегі 14-формуланы пайдаландық. Сонымен,
+C, мұнда бірінші қосылғышты алымы бөлімінің туындысы болғандай етіп түрлендірдік те 7-қасиетті пайдаландық. Ал екінші қосылғышта бөлімінің толық квадратын бөліп алып, интегралдар кестесіндегі 14-формуланы пайдаландық. Сонымен, 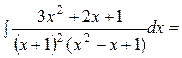
 ln| x+1 |-
ln| x+1 |- 

 +
+  +C.
+C.
Не нашли, что искали? Воспользуйтесь поиском: