
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Составляем симплексную таблицу, соответствующую исходной задаче
| X1 | X2 | … | Xn-1 | Xn | b | |
| F | -a0,1 | -a0,2 | … | -a0,n-1 | -a0,n | -b0 |
| Xn+1 | a1,1 | a1,2 | …. | a1,n-1 | a1,n | b1 |
| Xn+2 | a2,1 | a2,2 | … | a2,n-1 | a2,n | b2 |
| … | … | … | … | .. | … | … |
| Xn+m | am,1 | am,2 | … | am,n-1 | am,n | bm |
Шаг 1. Проверка на допустимость. Шаг 2. Проверка на оптимальность. Правила преобразований симплексной таблицы. При составлении новой симплекс-таблицы в ней происходят следующие изменения: Вместо базисной переменной xk записываем xl; вместо небазисной переменной xl записываем xk. ведущий элемент заменяется на обратную величину ak,l'= 1/ak,l все элементы ведущего столбца (кроме ak,l) умножаются на -1/ak,l все элементы ведущей строки (кроме ak,l) умножаются на 1/ak,l оставшиеся элементы симплекс-таблицы преобразуются по формуле ai,j'= ai,j- ai,lx ak,j/ ak,l
25.Формулировка двойственной задачи линейного программирования.Пары двойственных задач и их свойства. Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Если задана каноническая задача ЛП 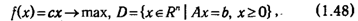 то задача ЛП
то задача ЛП  называется двойственной по отношению к ней. Свойства двойственных задач Теорема 1. Для пары двойственных задач верно соотношение
называется двойственной по отношению к ней. Свойства двойственных задач Теорема 1. Для пары двойственных задач верно соотношение 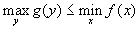 Следствие 1. Если в одной задаче из пары двойственных задач целевая функция неограничена, то во второй задаче допустимая область пуста.Следствие 2. Если для планов и исходной и двойственной задач выполняется соотношение
Следствие 1. Если в одной задаче из пары двойственных задач целевая функция неограничена, то во второй задаче допустимая область пуста.Следствие 2. Если для планов и исходной и двойственной задач выполняется соотношение  то они являются оптимальными планами соответствующих задач.Теорема 2. Для пары двойственных задач имеет место соотношение
то они являются оптимальными планами соответствующих задач.Теорема 2. Для пары двойственных задач имеет место соотношение  Теорема 3. (В формулировке для несимметричной двойственной задачи) Если i-ая компонента оптимального плана исходной задачи строго положительна, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана превращается в строгое равенство
Теорема 3. (В формулировке для несимметричной двойственной задачи) Если i-ая компонента оптимального плана исходной задачи строго положительна, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана превращается в строгое равенство 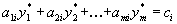 Если i-ая компонента оптимального плана исходной задачи равна нулю, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана имеет вид.
Если i-ая компонента оптимального плана исходной задачи равна нулю, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана имеет вид.
26.Экономическая трактовка транспортной задачи и ее математическая модель. Транспортная задача является частным типом задачи линейной Общая характеристика транспортной задачи Условие:Однородный груз сосредоточен у m поставщиков в объемах a1, a2,... am.Данный груз необходимо доставить n потребителям в объемах b1, b2... bn.Известны Cij, i=1,2,...m; j=1,2,...n — стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю.Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, и суммарные затраты на перевозку всех грузов являются минимальными. Исходные данные транспортной задачи записываются в виде таблицы:  Исходные данные задачи могут быть представлены в виде: вектора А=(a1,a2,...,am) запасов поставщиков,вектора B=(b1,b2,...,bn) запросов потребителей,матрицы стоимостей:
Исходные данные задачи могут быть представлены в виде: вектора А=(a1,a2,...,am) запасов поставщиков,вектора B=(b1,b2,...,bn) запросов потребителей,матрицы стоимостей: 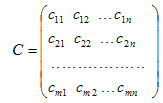 Математическая модель транспортной задачи Переменными (неизвестными) транспортной задачи являются xij, i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю.Эти переменные могут быть записаны в виде матрицы перевозок:
Математическая модель транспортной задачи Переменными (неизвестными) транспортной задачи являются xij, i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю.Эти переменные могут быть записаны в виде матрицы перевозок:  Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:
Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:  По условию задачи требуется обеспечить минимум суммарных затрат.Следовательно, целевая функция задачи имеет вид:
По условию задачи требуется обеспечить минимум суммарных затрат.Следовательно, целевая функция задачи имеет вид: 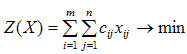 Система ограничений задачи состоит из двух групп уравнений.Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:
Система ограничений задачи состоит из двух групп уравнений.Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:  Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:
Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:  Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом:
Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом: 
27.Нахождение оптимального плана перевозок методом потенциалов. Метод потенциалов Наиболее простым методом ТЗ является метод потенциалов. Потенциалами называются условные числа Ui,Vj, приписанные определённым образом каждому поставщику и потребителю. Теорема(условия оптимального плана): Для того чтобы допустимый план перевозок 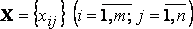 в транспортной задаче был оптимальным, необходимо и достаточно, чтобы существовали такие числа
в транспортной задаче был оптимальным, необходимо и достаточно, чтобы существовали такие числа 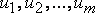 и
и  , что
, что  (1.1)
(1.1)  (1.2.) числа
(1.2.) числа  и
и 
 называют потенциалами пунктов отправления
называют потенциалами пунктов отправления  и
и 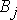 назначения соответственно. Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план. Для этого плана, в котором m + n – 1 базисных клеток, можно определить потенциалы
назначения соответственно. Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план. Для этого плана, в котором m + n – 1 базисных клеток, можно определить потенциалы  и так, чтобы выполнялось условие (1.1). Поскольку система (1.1) содержит m + n – 1 уравнений и m + n неизвестных, то одну из них можно задать произвольно (например, приравнять к нулю). После этого из m + n – 1 уравнений (1.1) определяются остальные потенциалы и для каждой из свободных клеток вычисляются величины
и так, чтобы выполнялось условие (1.1). Поскольку система (1.1) содержит m + n – 1 уравнений и m + n неизвестных, то одну из них можно задать произвольно (например, приравнять к нулю). После этого из m + n – 1 уравнений (1.1) определяются остальные потенциалы и для каждой из свободных клеток вычисляются величины  . Если оказалось, что
. Если оказалось, что 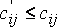 , то план оптимален.Если же хотя бы в одной свободной клетке
, то план оптимален.Если же хотя бы в одной свободной клетке 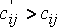 , то план не является оптимальным и может быть улучшен путем переноса по циклу, соответствующему данной свободной клетке.Циклом в таблице условий транспортной задачи, называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.Процесс улучшения плана продолжается до тех пор, пока не будут выполнены условия(1.2)
, то план не является оптимальным и может быть улучшен путем переноса по циклу, соответствующему данной свободной клетке.Циклом в таблице условий транспортной задачи, называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.Процесс улучшения плана продолжается до тех пор, пока не будут выполнены условия(1.2)
28. Постановка задачи динамического программирования. Динамическое программирование представляет собой метод оптимизации многошаговых процессов принятия решении, позволяющий указать пути исследования целого класса экстремальных задач. Постановку задачи динамического программирования рассмотрим на примере инвестирования, связанного с распределением средств между предприятиями. В результате управления инвестициями система последовательно переводится из начального состояния S0 в конечное Sn. Предположим, что управление можно разбить на n шагов и решение принимается последовательно на каждом шаге, а управление представляет собой совокупность n пошаговых управлений. На каждом шаге необходимо определить два типа переменных: переменную состояния системы Sk и переменную управления xk. Переменная Sk определяет, в каких состояниях может оказаться система на рассматриваемом k-м шаге. В зависимости от состояния S на этом шаге можно применить некоторые управления, которые характеризуются переменной xk, которые удовлетворяют определенным ограничениям и называются допустимыми.Допустим, X = (x1, x2, …, xk, …, xn) – управление, переводящее систему из состояния S0 в состояние Sn, a Sk – есть состояние системы на k-м шаге управления. Тогда последовательность состояний системы можно представить в виде графа, изображенного на рис. 1. x1 x2 xk-1 xk xk+1 xn S0 → S1 →... → Sk-1 → Sk →... → Sn Рисунок 1 – График состояний системы Применение управляющего воздействия xk на каждом шаге переводит систему в новое состояние S1(S, xk) и приносит некоторый результат Wk (S, xk). Для каждого возможного состояния на каждом шаге среди всех возможных управлений выбирается оптимальное управление х*k, такое, чтобы результат, который достигается за шаги с k-го по последний n-й, оказался бы оптимальным. Числовая характеристика этого результата называется функцией Беллмана Fk (S) и зависит от номера шага k и состояния системы S.Задача динамического программирования формулируется следующим образом: требуется определить такое управление Х*, переводящее систему из начального состояния S0 в конечное состояние Sn, при котором целевая функция принимает наибольшее (наименьшее) значение F(S0, X*) → extr. В основе метода динамического программирования лежит принцип оптимальности, впервые сформулированный в 1953 г. американским математиком Р. Э. Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая выигрыш на данном шаге. При решении задачи на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Если считать все шаги независимыми, тогда оптимальным управлением будет то управление, которое обеспечит максимальный выигрыш именно на данном шаге.
29.Постановка задачи нелинейного программирования. Общая задача нелинейного программирования (ОЗНП) определяется как задача нахождения максимума (или минимума) целевой функции f(x1, х2,..., xn) на множестве D, определяемом системой ограничений  где хотя бы одна из функций f или gi является нелинейной.
где хотя бы одна из функций f или gi является нелинейной.
По аналогии с линейным программированием ЗНП однозначно определяется парой (D, f) и кратко может быть записана в следующем виде  Перечислим свойства ЗНП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования:1. Множество допустимых планов D может иметь очень сложную структуру (например, быть невыпуклым или несвязным).2. Глобальный максимум (минимум) может достигаться как внутри множества D, так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов).3. Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа.
Перечислим свойства ЗНП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования:1. Множество допустимых планов D может иметь очень сложную структуру (например, быть невыпуклым или несвязным).2. Глобальный максимум (минимум) может достигаться как внутри множества D, так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов).3. Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа.
| <== предыдущая лекция | | | следующая лекция ==> |
| В трехмерном пространстве в декартовой системе координат любое линейное уравнение определяет плоскость | | |
Не нашли, что искали? Воспользуйтесь поиском: