Начала математического анализа

1. Постройте касательную к параболе:

а. 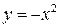в точке ;

б. в точке .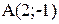

2. Найдите производную функции:

а. ;

б. ;

в. ;

г. ;

д. ;

е. .

3. Найдите производную функции:

а. в точке ;

б. в точке .

4. Запишите уравнение касательной к графику функции:

а. в точке ;

б. 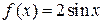в точке с абсциссой .

5. Найдите промежутки монотонности функции:

а. ;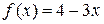

б. ;

в. ;

г. .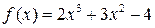

6. Найдите точки экстремума и экстремумы функции:

а. ;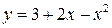

б. .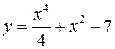

7. Вычислите интеграл:

а. ;

б. .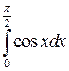

8. Найдите площадь фигуры, ограниченной линиями:

а. ;

б. .

Геометрия

1. Изобразите куб 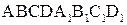и укажите:

а. прямые, параллельные прямой ;

б. прямые, пересекающиеся с прямой ;

в. прямые, скрещивающиеся с прямой ;

г. плоскость, параллельную плоскости .

2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые:

а. пересекаться;

б. быть параллельными;

в. быть скрещивающимися?

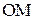3. Через точку пересечения диагоналей прямоугольника проведена прямая , перпендикулярная плоскости прямоугольника. Найдите длину отрезка , если , , .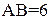

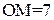4. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми . Найдите наклонную и её проекцию на плоскость, если длина перпендикуляра 5 см.

5. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны 7, 9 и .

6. В правильной четырёхугольной пирамиде сторона основания равна 4 см, а угол наклона боковой грани к плоскости основания равен . Найдите площадь боковой поверхности пирамиды.

7. Основанием прямой призмы является равносторонний треугольник со стороной 6 см. Высота призмы равна 4 см. Найдите площадь поверхности призмы.

8. Апофема правильной шестиугольной пирамиды равна 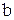, а радиус описанной около основания окружности равен . Найдите площадь боковой поверхности этой пирамиды.

9. Что представляет собой сечение цилиндра плоскостью, проходящей:

а. через две образующие;

б. через некоторую точку поверхности перпендикулярно оси?

10. Что представляет собой сечение конуса плоскостью, проходящей:

а. через ось конуса;

б. через точку поверхности перпендикулярно оси;

в. через две образующие?

11. Сколько квадратных метров листовой жести пойдёт на изготовление трубы длиной 3 м и диаметром 40 см, если на швы необходимо добавить 2% площади её боковой поверхности?

12. Найдите высоту конуса, если площадь его осевого сечения равна 10 см²,а площадь основания равна 6 см².

13. Игрушечное ведёрко имеет форму усечённого конуса, радиусы оснований которого равны 7 см и 13 см, а образующая равна 10 см. Найдите:

а. высоту ведёрка;

б. массу краски, необходимой для окраски этого ведёрка с обеих сторон, если на окраску 1 см² требуется 0,2 г краски.

14. Площадь сечения сферы, проходящего через её центр равна 7 дм². Найдите площадь поверхности сферы.

15. Диагональ прямоугольного параллелепипеда равна 12 см и составляет угол с плоскостью основания и с ребром основания. Найдите объём параллелепипеда.

16. Найдите объём правильной треугольной пирамиды:

а. высота которой 10 см, а сторона основания 6 см;

б. апофема которой равна 8 см и составляет с плоскостью основания.

17. Какова вместимость цистерны, имеющей форму цилиндра с диаметром 4 м и длиной 10 м?

18. Найдите объём конуса, имеющего высоту h, равную диаметру основания.

19. Стороны оснований правильной усечённой четырёхугольной пирамиды равны 10 см и 18 см, апофема равна 5 см. Найдите объём усечённой пирамиды.

20. Найдите массу метеорита, имеющего форму шара радиуса 1 м, если плотность составляющего её вещества равна 3 г/см³.

Cтохастика (комбинаторика, теория вероятностей и математическая статистика)

1. Сколько различных смешанных пар для игры в теннис можно образовать из 5 юношей и 6 девушек?

2. Записать всевозможные двузначные числа, образованные с помощью цифр 0, 4, 8.

3. Найдите: ; ; .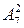

4. Сколькими способами можно обозначить вершины данного треугольника, используя буквы А, В, С, D, E, F?

5. Сколько различных шестизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 2, 3, 4, 5, 6 и 7 так, чтобы:

а. последней была цифра 2;

б. запись каждого из них начиналась с 65?

6. Сколько различных букетов из трёх цветков можно составить, выбирая из имеющихся 10 цветков?

7. Бросается игральный кубик, грани которого пронумерованы числами от 1 до 6. Какова вероятность того, что выпадет:

а. число 5;

б. чётное число;

в. число 8;

г. натуральное число;

д. число, не меньшее 5?

8. Бросаются для игральные кости. Какова вероятность того, что сумма выпавших очков равна 4?

9. Вероятность попадания по цели стрелком при одном выстреле равна 0,91. Какова вероятность того, что этот стрелок промахнётся, сделав один выстрел?

10. Стрелок попал в цель 38 раз, сделав 50 выстрелов. Найдите частоту попадания стрелком в цель рассмотренной серии выстрелов.

11. Из колоды в 36 карты наугад вынимают три карты. Какова вероятность того, что все вынутые карты трефовой масти?

12. В октябре учитель записал число полных лет каждого учащегося выпускного класса: 16, 17, 16, 15, 16, 17, 16, 16, 16, 15, 16, 17, 14, 16, 16, 17, 16, 17, 16, 16. Составить частотную таблицу полных лет учащихся. Полученные результаты представить в виде полигона частот. Найдите средний возраст учащихся класса.

13. Найдите среднее арифметическое, моду, медиану и размах выборки:

а. 5, 5, 5, 6, 7, 7;

б. 2, 3, 1, 4, 2, 1, 5.

[1] Издания, отмеченный знаком *, имеются в фондах библиотеки РАП.

[2] Задания, отмеченные знаком * не подлежат обязательному контролю

Не нашли, что искали? Воспользуйтесь поиском: