ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Вказівки до розв’язування задач

⇐ Предыдущая 86 87 88 89 90 91 92 93 9495

Типового варіанту

До задачі 1

Варіант 0:

Розв’язання. а) Позначимо рівняння системи:

Вписуємо елементи системи в обчислювальну таблицю (див. 1.1, табл.1, або приклад 1, табл.2)

Nп/п	X₁	X₂	X₃	Вільни члені	Суми	Контроль
			-1	-5	-2
			-5	-3	-3
	-2	-1
		-7	-2
				-9	-3	-3

Зворотний хід. Виписуємо трикутну систему згідно з рядками1, 4, 6, куди входять провідні елементи

З другого рівняння трикутної системи

З першего рівняння

Відповідь:

б) Обчислимо визначники: За формулами Крамера:

в) Позначення А — матриця системи, В — стовпець вільних членів, Х — стовпець невідомих:

Матричний вигляд системи: АХ=В. Розв’язання цього рівняння (за умови існування оберненої матриці А ^-1):

Формула оберненої матриці:

якщо то

де D ¹ 0 - визначник матриці А; А _ij — алгебраїчне доповнення до елементу а _ij матриці А.

У цій задачі D = 3 Þ А ^-1 існує. Обчислюємо А _ij:

До задачі 2

Варіант 0:

Відповіді і вказівки.

(12)Використати скалярний добуток векторів (умову ортогональності). Відповідь: t =

(13)Три вектори утворюють базис тільки тоді, коли визначник, складений з кординат цих векторів, відмінний від 0:

Нехай - координати у новому базисі: .

Виконуючи дії з координатами, перепишемо цю рівність у координатному вигляді:

Розв’язок системи:

Відповідь

До задачі 3

Варіант 0:

Відповіді та вказівки.

(8) Розглянути вектори

За властивістю бісектриси відстані довільної її точки N (x,y) до сторін АВ і АС рівні: Відомо, якщо то або . Тому слід розглянути два випадки: Одна з цих прямих — бісектриса внутрішнього кута, а друга —зовнішнього. Відп.: х + 3 у = 4. Див. рис. 1.

Рис. 1

До задачі 4

Варіант 0:

Розв’язання та відповіді. (1) Див. Рис. 2.

Масштаб на Ох удвічі менше, ніж на Оy і Oz.

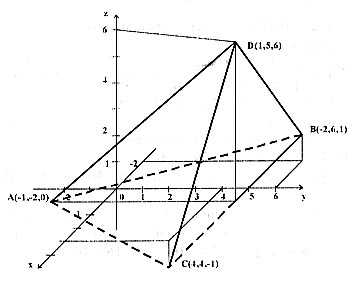
Рис. 2.

(5) Дослідження загального рівняння площини. Відп.: площина АВС паралельна вісі Оy.

(6) Нормальний вектор площини (Р) — векторний добуток напрямного вектора прямої ВС та нормального вектора площини xOy. Відп.: x + 3 y = 16. Інший спосіб. Скористатися рівнянням площини, що продить через три точки D, С і С ₁ (4,4,0).

— нормальний вектор площини (Q); скласти рівняння площини за точкою А та вектором . Вiдп.:

(11)Очевидно, відстань між АD і BC дорівнює відстані від точки B до (Q). Відп.:

(12)

(13) — прекції точок В і С на хОy. Рівняння прямої ,

Відповідь

Інший спосіб. Оскільки то проекція – перетин площин

(Р) і xOy:

Як бачимо, параметричні рівняння можуть бути подані у різному вигляді. Пропонуємо з’ясувати, чи належить точка Е до прямої В ₁ С ₁.

(14)

До задачі 5

Варіант 0:

Розв’язання. а) Парабола. Рівняння перетворити до вигляду:

Точка (- 2;1) — вершина параболи. Визначити напрям віток. Для точнішої побудови лінії додатково обчислити декілька точок, наприклад, та ін. Пряма х = - 2 — вісь симетрії. Див. рис. 3.

б) Гіпербола. Канонічне рівняння

Півосі Фокуси на осі Оy. Рівняння асимптот Визначити вершини гіперболи. Використовуючи формулу додатково обчислити декілька точок лінії, наприклад, та ін. (При побудові прийняти:

) Див. Рис. 4.

Рис. 4.

в) Еліпс. Канонічне рівняння Півосі а = 2, b = 4. Фокуси на осі Oy. Визначити вершини еліпса. Використовуючи формулу , додатково знайти декілька точок еліпса, наприклад, та ін. Див. Рис. 5.

До задачі 6

Розв’язання. а) Оскільки то рівняння зводиться до вигляду:

— еліпсоїд з центром у точці (0,3,0) і півосями а = 1, b = 4, c =1; див. Рис. 6.

б) Гіперболічний циліндр, див. рис. 7. У площині xOy побудувати гіперболу . Поверхня, утворена твірними паралельними вісі Oz. Що проходять через дану гіперболу.

в) Гіперболічний параболоїд, див. рис. 8. Прямі UT і RS — перерізи поверхні площиною xOy. Знайти рівняння цих прямих (у площині xOy). Упевнитися, що перерізи площинами yOz і xOz — параболи APOLB і COD. Ці параболи дотикаються осей Oy і Oz. Які лінії утворюють перерізи площинами ? Визначити тип цих ліній. Довести, що перерізи площинами — гіперболи KLM, NPQ та GCH, FDE.

Рис.8

До задачі 7

Варiант 0:

Розв'язання. а) Тіло обмежене параболічними циліндрами

площиною , паралельною осі Ox, і площиною xOy; див. рис. 9.

б) Тіло обмежене конусом , площиною x + z = 1, паралельною осі Oy, і координатними площинами xOy (z = 0), yOz (x = 0), xOz (y = 0); див. Рис. 10. Звернути увагу нав переріз конуса площиною x + z = 1.

Рис.10

До задачі 8

Варіант 0:

Розв’язання. а) Знайдемо для якого

Можна упевнитися, що при

Далі складемо таблицю значень

	0,6		1,3	1,5	1,9	...	0,3
	-10					...

Для задовільної побудови лінії таблиця повинна мати достатню кількість значень.

Нехай Ох — полярна вісь. Масштаб: 1.

Будуємо точки лінії: на стороні кута відкладаємо 0,6, на Ох — 1, на стороні кута і т. д. Одержані точки сполучаємо плавною лінією. Промені і дотикаються лінії у точці О. Див. мал. 14.