Методы определения исходного базисного решения

I. Метод «северо-западного угла»

Распределение поставок начинают от первого поставщика к первому потребителю . Если , то весь груз от поставляют , а затем от второго поставщика доставляют недостающий груз потребителю . Оставшийся груз от поставляют второму потребителю и т.д. Если , то полностью удовлетворяют потребности первого потребителя . Оставшийся груз поставляют второму потребителю , стараясь полностью удовлетворить его потребности. В противном случае недостающий груз поставляют от второго поставщика и т.д. Распределение груза производится до тех пор, пока не будет вывезен весь груз, а все потребители не будут полностью удовлетворены. Величину поставки от - ого поставщика к - му потребителю записывают в нижнем правом углу соответствующей клетки. Заполненные клетки в распределительной таблице соответствуют базисным переменным, а свободные клетки – свободным переменным, они перечеркиваются. Заполненных клеток в опорном решении должно быть , так как в системе ограничений такое количество линейно независимых уравнений. Если получим заполненных клеток меньше, чем , то решение будет вырожденным. Чтобы этого не было, искусственно загружают одну (недостающую) клетку нулевым грузом.

Определение. Циклом в матрице (таблице) будем называть ломаную с вершинами в клетках и звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющей условиям:

1) ломаная должна быть связной, то есть из любой её вершины можно попасть в любую другую вершину по звеньям ломаной;

2) в каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, другое – по столбцу.

Пример 1.

Опорный план: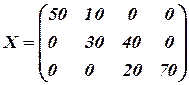

.

Следовательно, закрытая модель транспортной задачи.

Заполненных клеток в данном случае , т.е. решение не вырожденное. Стоимость перевозок при этом плане

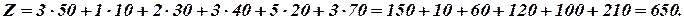
II. Метод «наименьшей стоимости»

Суть метода заключается в том, что каждый раз заполняется клетка с наименьшей издержкой .

В таблице выбирается клетка с наименьшей издержкой . Если 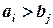в этой клетке, то и потребности потребителя удовлетворены полностью, т.е. все остальные клетки j- го столбца вычеркиваются.

Если 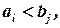то и ресурсы поставщика полностью израсходованы, т.е. все остальные клетки i - ой строки вычеркиваются.

Далее в таблице опять выбирается свободная и не вычеркнутая клетка с наименьшей издержкой . Она аналогично заполняется, но теперь еще с учетом системы ограничений задачи (т.е. сумма по строкам должна быть равна , сумма по столбцам − ).

Заполненных клеток должно быть . Если их меньше, то одновременно на некотором шаге были удовлетворены и поставщик и потребитель , и одновременно были вычеркнуты и i - ая строка и j -ый столбец. В этом случае дается нулевая (фиктивная) поставка в произвольную, но не вычеркнутую клетку соответствующего столбца или соответствующей строки, которые должны быть вычеркнутыми на этом шаге.

Пример 2.

Опорный план: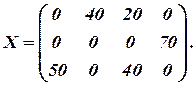

Заполненных клеток оказалось 5: исходное решение вырожденное, т.е. мы должны были дать фиктивную поставку, когда заполняли клетку 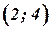и были вычеркнуты одновременно и строка и столбец.

Стоимость перевозок при этом плане:

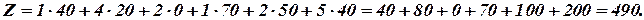
Это меньше, чем по методу «северо-западного угла» ().

Критерий оптимальности. Метод потенциалов

Для того чтобы допустимое решение было оптимальным необходимо и достаточно, чтобы существовала совокупность действительных чисел 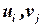, которые удовлетворяли бы условиям:

для заполненных клеток

для свободных (вычеркнутых) клеток.

Числа 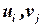называются потенциалами.

Оценить опорное решение с помощью потенциалов можно следующим образом: первоначально одному из потенциалов или дается значение 0. Затем находятся остальные потенциалы из равенств (по заполненным базисным клеткам).

Оценки свободных клеток вычисляются по формуле: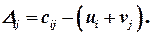

Если все 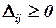, то задача решена и исходное опорное решение оптимальное. Если есть хотя бы одна отрицательная оценка, то решение можно улучшить, перейдя к другому опорному решению. Новое опорное решение нужно вновь оценить с помощью потенциалов.

Пример 3 (по методу «северо-западного угла»).

50               40                     −2 −1 −3

Матрица оценок для данного решения имеет вид

.

Так как , то решение не оптимально. При переходе к другому опорному решению необходимо выполнить однократное замещение одной из базисных переменных на свободную переменную.

Нас не устраивает оценка клетки , поэтому введем в базис свободную переменную . Соответственно при этом клетка должна быть заполненной. Пусть поставка в ней будет . Тогда нарушается баланс в третьей строке и первом столбце. Восстановить его можно, уменьшив поставки и (поставку не затрагиваем, так как нарушенный баланс в четвертой строке восстановить не удастся). Получим новые поставки и . Далее нарушается баланс в первой строке и третьем столбце. Для его восстановления изменяем на единиц поставки в клетках и , а именно . Аналогично нарушается баланс во второй строке и во втором столбце, который может быть восстановлен путем изменения поставки 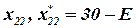. Таким образом, добавляя поставку к клеткам , получим другое решение задачи:

.

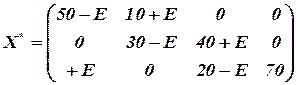В таблице или отдельно вычерчивается контур, по которому распределяются поставки . Полученный контур является замкнутым многоугольником у которого:

1) все углы прямые;

2) четное число вершин;

3) в вершинах расположены заполненные клетки, кроме одной, которую решили заполнить числом ;

4) при движении по контуру вершины, в которых добавляется и вычитается поставка , чередуются.

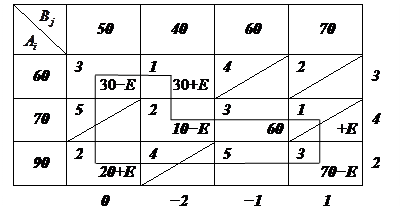
В качестве поставки выбирается минимум среди поставок, из которых E вычиталось. В нашем случае . Тогда мы получим новое опорное решение, которое вновь оценим

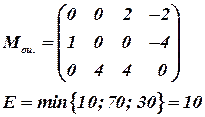
На следующем шаге будем иметь

	20−E     +E         60       30+E     60−E       −2

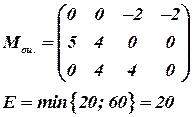
В итоге получим

	60                     −2

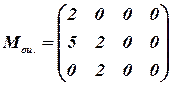
Критерий оптимальности выполнен: .

Следовательно, минимальная стоимость перевозок будет

Открытая модель транспортной задачи

Если 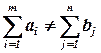, то транспортная задача называется открытой, математическая модель такой задачи не каноническая.

I случай. Если , т.е. производится больше, чем потребляется, тогда модель транспортной задачи будет иметь вид: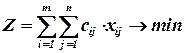

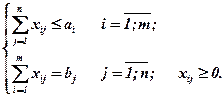
II случай. Если , т.е. потребность больше, чем производство, тогда модель задачи: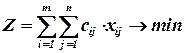

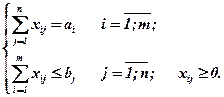
Чтобы решить открытую задачу, нужно привести ее к каноническому виду.

В I случае вводят фиктивного потребителя , потребности которого . Во II случае вводят фиктивного поставщика , запасы которого

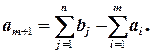
Транспортные издержки клеток, соответствующих фиктивному поставщику или потребителю, принимают наибольшей из всех транспортных издержек или равным 0.

Пример 4.

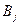
потребляется меньше, чем производится

Следовательно, вводим фиктивного потребителя , для которого . Методом наименьшей стоимости найдем первое решение.

I шаг

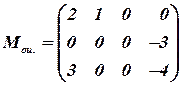
Строим цикл для клетки

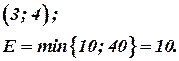
II шаг

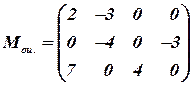
Строим цикл для клетки

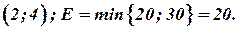
III шаг

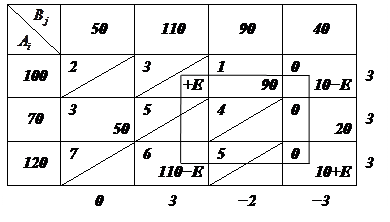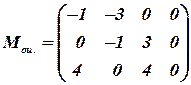
Строим цикл для клетки

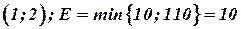
IV шаг

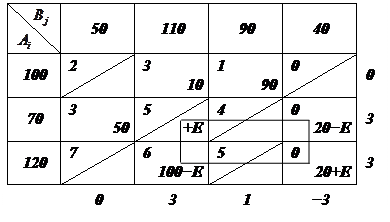
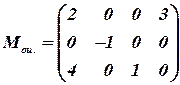
Строим цикл для клетки

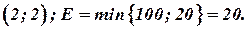
V шаг

	−4

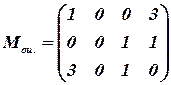
Критерий оптимальности выполнен.

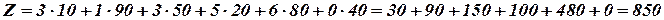
Список используемой литературы

Не нашли, что искали? Воспользуйтесь поиском: