Условные обозначения логических связок

Связка	Операция	Обозначение	Правила чтения	Пример А, В – преподаватель ведет практику
Не	Отрицание		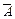Не А	­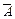– преподаватель не читает лекции, – Преподаватель не ведет практику
И	Конъюнкция		А и В	– Преподаватель читает лекции и (преподаватель) ведет практику
Или	Дизъюнкция		А или В	– Преподаватель читает лекции или (преподаватель) ведет практику
Если…, то …	Импликация		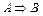Если А, то В	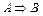– Если преподаватель читает лекции, то он (преподаватель) ведет практику
…, тогда и только тогда, когда	Эквиваленция		А тогда и только тогда, когда В	Преподаватель читает лекции тогда и только тогда, когда он(преподаватель) ведет практику

1. Отрицание высказывания

Определение 1. Отрицанием высказывания Р называется новое высказывание, обозначаемое 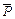(читается: «Не Р» или «Неверно, что Р»), которое считается истинным, если высказывание Р ложно, и ложным, если Р истинно.

Иначе говоря, значения истинности высказываний Р и 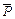связаны между собой, как указано в следующей таблице:

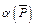
Эта таблица читается по строкам. Например, первая строка под горизонтальной чертой означает: если 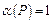, то 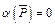. Приведенная таблица называется таблицей истинности для отрицания.

2. Конъюнкция высказываний

Определение 2. Конъюнкцией высказываний Р и Q называется новое высказывание, обозначаемое 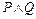(читается «Р и Q»), которое считается истинным, если истинны оба высказывания Р и Q, и ложным во всех остальных случаях.

Таким образом, значение истинности высказывания 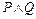связано со значениями истинности высказываний Р и Q. Эта связь выражается таблицей:

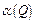
Приведенная таблица называется таблицей истинности для конъюнкции.

Данное выше определение конъюнкции вполне отвечает тому смыслу, который придается в рассуждениях союзу «и». Действительно, привычная логика рассуждений требует, чтобы утверждение «Р и Q» было истинно лишь в одном случае: когда истинны оба утверждения Р и Q.

Примеры.

1. Высказывание «Число 2 четное и простое» является конъюнкцией высказываний: «Число 2 четное» и «Число 2 простое». Так как оба последних высказывания истинны, то истинна и их конъюнкция.

2. Высказывания «2 меньше 5» и «5 меньше 10» истинны, поэтому истинна и их конъюнкция «2 меньше 5 и 5 меньше 10». Последнее высказывание записывают обычно так: «2<5<10».

3. Дизъюнкция высказываний

Определение 3. Дизъюнкцией высказываний Р и Q называется новое высказывание, обозначаемое 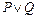(читается «Р или Q»), которое истинно в тех случаях, если истинно хотя бы одно из высказываний Р или Q, и ложно, если ложны оба высказывания Р и Q.

Значение истинности высказывания 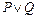связано со значениями истинности высказываний Р и Q с помощью таблицы:

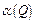
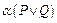
Эта таблица называется таблицей истинности для дизъюнкции.

Приведенное определение дизъюнкций вполне отвечает обычному употреблению союза «или». Действительно, в практике рассуждений утверждение «Р или Q» считается верным в любом из случаев, когда верно Р или Q; если же оба утверждения Р и Q неверны, то неверно и «Р или Q».

Примеры.

1. Высказывание «В неделе 10 дней или в году 12 месяцев» является дизъюнкцией двух высказываний: «В неделе 10 дней» и «В году 12 месяцев». Несмотря на кажущуюся странность такого высказывания, мы все же признаем его истинным, поскольку истинно одно из составляющих его высказываний («В году 12 месяцев»).

2. Высказывание «2<3» является дизъюнкцией высказываний «2<3» и «2=3», из которых первое истинно, а второе ложно. Следовательно, истинна и сама дизъюнкция.

4. Импликация высказываний

Определение 4. Импликацией высказываний Р и Q называется высказывание, обозначаемое (читается: «Если Р, то Q», или «Из Р следует Q», или «P влечет за собой Q»), которое ложно лишь в том случае, если Р истинно, a Q ложно.

Таблица истинности для импликации имеет вид

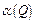
Данные выше определение импликации в основном отражает тот смысл, который придается в обычных рассуждениях связке «если..., то...». Единственное возражение может вызвать, пожалуй, лишь та строка таблицы, где 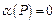, , 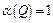. Однако с таким пониманием импликации приходится все же согласиться, поскольку принцип «Из лжи следует что угодно» представляется вполне оправданным.

Заметим, что при рассмотрении импликации P=>Q высказывание Р называют посылкой (или условием) импликации, а высказывание Q – ее заключением (или следствием).

Примеры.

1. Высказывание «Если Земля круглая, то » является импли­кацией высказываний «Земля круглая» и «». Оно истинно, так как истинны оба последних высказывания.

2. Высказывание «Если , то число 5 – простое» есть импликация выска­зываний «» и «5 – простое». Оно истинно, поскольку посылка «» – Ложное высказывание.

5. Эквивалентность высказываний

Определение 5. Эквивалентностью (или эквиваленцией) высказываний Р и Q называется новое высказывание, обозначаемое 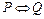(читается «P эквивалентно Q», или «P тогда и только тогда, когда Q»), которой истинно в том и только в том случае, если Р и Q одновременно Истинны или одновременно ложны.

Таблица истинности для эквивалентности выглядит следующим образом:

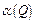
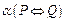
Примеры.

1. Высказывание «2 2 = 4» тогда и только тогда, когда Земля – шар" представляет собой эквиваленцию двух высказываний: «2 2 = 4» и «Земля – шар». Оно истинно, поскольку истины оба этих высказывания.

2. Высказывание «Небо синее в том и только в том случае, когда снег черный» является эквиваленцией высказываний «Небо синее» и «Снег черный». Оно ложно, так как одно из двух последних высказываний истинно, а другое ложно.

6. Логические операции как операции на множестве

Рассмотрим любую из логических операций, например операцию конъюнкции 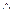. Поскольку число полностью определяется числами и 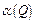, мы можем оперировать не с высказываниями, а с числами 0 и 1, определив конъюнкцию

над ними с помощью таблицы

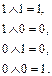
Аналогичные замечания можно сделать и по отношению к остальным логическим операциям.

Например, 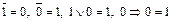и т. д.

Таким образом, каждой логической операции над высказываниями соответствует некоторая функция, определенная на двухэлементном множестве и принимающая значения в том же множестве. Эту функцию мы будем называть тем же термином (отрицание, конъюнкция, дизъюнкция и т.д.), что и соответствующую логическую операцию.

Не нашли, что искали? Воспользуйтесь поиском: