
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Формулы алгебры высказываний
1. Определение и примеры формул
С помощью логических операций, рассмотренных в предыдущем параграфе, можно, исходя из простейших высказываний, строить новые, более сложные. Например, исходя из высказываний Р: «Пушкин – русский поэт», Q: «Гаусс – немецкий математик», R: « », можно построить новое высказывание: «Если Пушкин – русский поэт и Гаусс – немецкий математик, то
», можно построить новое высказывание: «Если Пушкин – русский поэт и Гаусс – немецкий математик, то  ». Это новое высказывание имеет вид
». Это новое высказывание имеет вид
 . (1)
. (1)
Выражение (1), если отвлечься от конкретного смысла высказываний Р, Q, R, можно рассматривать как некоторую схему, позволяющую, исходя из любых высказываний Р, Q, R, строить новое высказывание. Именно такие схемы и будут нас сейчас интересовать. Они называются формулами алгебры высказываний. Мы, конечно, привыкли к несколько другому толкованию понятия «формула»; для нас формулы – это равенства типа  (формула площади круга),
(формула площади круга),  (формула, выражающая теорему Пифагора) и т. д. Тем не менее выражение
(формула, выражающая теорему Пифагора) и т. д. Тем не менее выражение  также можно рассматривать как своего рода формулу – формулу конструирования составного высказывания из более простых.
также можно рассматривать как своего рода формулу – формулу конструирования составного высказывания из более простых.
Прежде чем дать общее определение формулы алгебры высказываний, условимся о нижеследующем. Высказывательными переменными будем называть такие переменные, которые могут принимать в качестве своих значений любые конкретные высказывания. Будем обозначать такие переменные заглавными латинскими буквами X, У, Z, U, V,..., или теми же буквами с индексами:  Введем, кроме того, еще две специфические высказывательные переменные И и Л; вместо первой можно подставлять любое истинное высказывание, вместо второй – любое ложное.
Введем, кроме того, еще две специфические высказывательные переменные И и Л; вместо первой можно подставлять любое истинное высказывание, вместо второй – любое ложное.
Полное описание понятия формулы дают следующие соглашения:
1°. Каждая отдельно взятая высказывательная переменная есть формула.
2°. Если  и
и 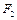 – две формулы, то выражения
– две формулы, то выражения  ,
, 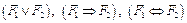 также являются формулами.
также являются формулами.
3°. He существует никаких других формул, кроме тех, которые получаются в результате применения конечного числа раз пп.1° и 2°.
Так, например, формулами являются следующие выражения:  и т.д.
и т.д.
Для большей отчетливости укажем примеры выражений, не являющихся формулами: 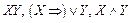 .
.
То, что мы не признаем формулой последнее из написанных выражений, может вызвать сначала недоумение. Однако если строго следовать данному выше определению, то выражение  – не формула; чтобы стать формулой, ему не хватает скобок, так как, согласно п. 2°, формулой должно быть выражение
– не формула; чтобы стать формулой, ему не хватает скобок, так как, согласно п. 2°, формулой должно быть выражение  , а не
, а не  . Различие между выражениями
. Различие между выражениями  и
и  станет особенно существенным, если мы включим выражение
станет особенно существенным, если мы включим выражение  в качестве составляющей части в более сложную формулу: сравните, например, выражение
в качестве составляющей части в более сложную формулу: сравните, например, выражение  , являющееся формулой, с выражением
, являющееся формулой, с выражением  (не формулой); неясно, как следует понимать второе выражение (какая операция следует за какой:
(не формулой); неясно, как следует понимать второе выражение (какая операция следует за какой: 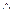 после
после  или
или  после
после 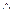 ?).
?).
Итак, запись внешних скобок у формулы будем считать необязательной, если только эта формула не входит составной частью в более сложную формулу.
2. Таблицы истинности для формул
Рассмотрим какую-нибудь формулу алгебры высказываний, например 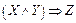 . Обозначим эту формулу сокращенно F(X, У, Z). Значение истинности формулы F(X, У, Z) полностью определяется значениями истинности переменных X, У, Z. Это обстоятельство позволяет составить таблицу, дающую значение истинности для F(X, У, Z) в зависимости от значений истинности для X, У, Z. Такая таблица должна состоять из четырех столбцов: трех – для переменных X, Y, Z и одного – для самой формулы. Так как каждая из переменных X, У, Z может принимать два значения (1 или 0), то для тройки X, У, Z получается
. Обозначим эту формулу сокращенно F(X, У, Z). Значение истинности формулы F(X, У, Z) полностью определяется значениями истинности переменных X, У, Z. Это обстоятельство позволяет составить таблицу, дающую значение истинности для F(X, У, Z) в зависимости от значений истинности для X, У, Z. Такая таблица должна состоять из четырех столбцов: трех – для переменных X, Y, Z и одного – для самой формулы. Так как каждая из переменных X, У, Z может принимать два значения (1 или 0), то для тройки X, У, Z получается  различных возможностей. Это означает, что таблица должна иметь 8 строк. Для заполнения последнего столбца таблицы подставляем значения X, У и Z в формулу F(X, У, Z). Например, при X = 1, У = 1, Z = 1 имеем
различных возможностей. Это означает, что таблица должна иметь 8 строк. Для заполнения последнего столбца таблицы подставляем значения X, У и Z в формулу F(X, У, Z). Например, при X = 1, У = 1, Z = 1 имеем
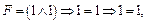
при X = 1, У = 1, Z = 0 находим

и т. д. В результате заполнения получаем следующую таблицу:

| 
| 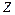
| 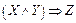
|
Вообще, для каждой формулы 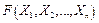 алгебры высказываний можно составить таблицу, дающую значение истинности формулы в зависимости от значений истинности переменных
алгебры высказываний можно составить таблицу, дающую значение истинности формулы в зависимости от значений истинности переменных  . Такая таблица называется таблицей
. Такая таблица называется таблицей
истинности для формулы 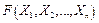
Процедуру составления таблицы истинности можно упростить, используя некоторые приемы. Проиллюстрируем это на следующем примере.
Пример. Составить таблицу истинности для формулы

(в силу принятого соглашения внешние скобки у формулы опущены).
Первый шаг заключается в установлении последовательности операций. Для этого над знаком каждой логической операции, встречающейся в формуле, ставим номер, означающий очередность выполнения этой операции. В данном случае возможна, например, такая нумерация: 
В первой (заглавной) строке таблицы запишем X, У, а также данную формулу. Под переменными X и У выписываем всевозможные наборы их логических значений. Тогда получим таблицу

| 
| 
|
| 1 1 | ||
| 0 0 | ||
| 1 1 | ||
| 1 0 |
которую продолжаем заполнять дальше. Под номером 1 запишем значения, принимаемые формулой 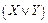 . Для соответствующих значений X и У. Затем точно так же заполняем столбцы под номерами 2, 3, 4, 5. В результате получаем следующую таблицу:
. Для соответствующих значений X и У. Затем точно так же заполняем столбцы под номерами 2, 3, 4, 5. В результате получаем следующую таблицу:

| 
| 
|
| 1 1 1 1 0 1 0 | ||
| 0 1 0 1 0 1 1 | ||
| 1 1 1 0 1 0 0 | ||
| 1 0 0 0 1 1 1 |
Столбец под номером 5 (полученный последним) дает значения истинности данной формулы.
3. Тавтологии
Определение 1. Формула 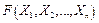 алгебры высказываний называется тождественно истинной (или тавтологией), если ее значение истинности равно 1 при любых значениях истинности для
алгебры высказываний называется тождественно истинной (или тавтологией), если ее значение истинности равно 1 при любых значениях истинности для  .
.
Роль тавтологий прежде всего заключается в том, что они дают схемы построения истинных высказываний, независимо от содержания и истинности составляющих высказываний.
Например, тавтологией является формула
 («X или не X»). Действительно, какое бы конкретное высказывание ни было подставлено вместо X, высказывание
(«X или не X»). Действительно, какое бы конкретное высказывание ни было подставлено вместо X, высказывание  истинно, поскольку
истинно, поскольку 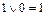 и
и 
Однако значение тавтологий состоит не только в том, что с их помощью строятся истинные высказывания; не меньшее значение имеет и то, что тавтологии дают правильные способы умозаключения. Проиллюстрируем это на примере формулы 
Эта формула является тавтологией; что легко проверяется, если составить для нее таблицу истинности (в столбце значений для всей формулы окажутся одни единицы). Схема логического умозаключения, выражаемая этой тавтологией; часто используется в математике: эта схема носит название «доказательство от противного». А именно, пусть требуется доказать некоторое утверждение X. Рассуждаем так: допустим, что X неверно (т. е. что верно 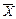 ). Далее с помощью некоторого рассуждения (в рамках той теории, которая изучается) доказываем, что из
). Далее с помощью некоторого рассуждения (в рамках той теории, которая изучается) доказываем, что из 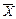 следует некоторое утверждение Y, а также – что из
следует некоторое утверждение Y, а также – что из 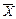 следует противоположное утверждение
следует противоположное утверждение  . Так как одновременная справедливость утверждений
. Так как одновременная справедливость утверждений  и Y невозможна, то из проведенного рассуждения делаем вывод о справедливости (истинности) X.
и Y невозможна, то из проведенного рассуждения делаем вывод о справедливости (истинности) X.
Укажем некоторые особо важные тавтологии.
1. Законы коммутативности конъюнкции и дизъюнкции:
 .
.
2. Законы ассоциативности конъюнкции и дизъюнкции:
 .
.
3. Законы дистрибутивности:

 .
.
4. Законы де Моргана:  .
.
5. Закон исключенного третьего:  .
.
6. Закон контрапозиции: 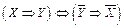 .
.
7. Правило цепного заключения (закон силлогизма):
 .
.
8. Правило «модус поненс»:  .
.
9. Схема доказательства «от противного»:  .
.
Доказательство того, что каждая из указанных формул является тавтологией, провести самостоятельно в качестве упражнения.
4. Равносильность формул
Определение 2. Две формулы 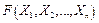 и
и  алгебры высказываний называются равносильными, если при любых логических значениях переменных
алгебры высказываний называются равносильными, если при любых логических значениях переменных  логические значения высказываний F и H совпадают. Равносильность формул F и H записывается так:
логические значения высказываний F и H совпадают. Равносильность формул F и H записывается так:  .
.
Существует тесная связь между понятием равносильности формул и понятием тавтологии. Она заключается в следующем: формулы F и Н равносильны тогда и только тогда, когда формула  является тавтологией.
является тавтологией.
Справедливость этого утверждения следует непосредственно из самих определений
равносильности формул и тавтологии.
Примеры.
1. Доказать равносильность формул  и
и  .
.
Для каждой из данных формул составим таблицу истинности:

| Y | 
| 
| Y | 
| |
Сравнивая таблицы, видим, что указанные формулы равносильны.
2. Доказать равносильность формул 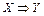 и
и  .
.
Разумеется, можно сравнить таблицы истинности данных формул! Однако можно рассуждать и так: формула 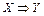 ложна лишь в случае Х= 1, Y = 0, а формула
ложна лишь в случае Х= 1, Y = 0, а формула  – лишь в случае X = О, Y = 0, т. е. при Х= 1, Y = 0. Таким образом, обе формулы ложны или истинны одновременно.
– лишь в случае X = О, Y = 0, т. е. при Х= 1, Y = 0. Таким образом, обе формулы ложны или истинны одновременно.
Целый ряд равносильностей можно получить, исходя из приведенных в п. 3 тавтологий. Например, формулы  и
и 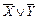 равносильны, поскольку формула
равносильны, поскольку формула  является тавтологией (см. тавтологии 4°).
является тавтологией (см. тавтологии 4°).
Следует заметить, что выражение  не является формулой. Оно представляет собой просто запись того факта, что между формулами F и H имеется определенного рода связь (а именно, что F равносильна H).
не является формулой. Оно представляет собой просто запись того факта, что между формулами F и H имеется определенного рода связь (а именно, что F равносильна H).
Не нашли, что искали? Воспользуйтесь поиском: