Лекция 6. ДЕДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ

1. Простой категорический силлогизм и правила его построения.

2. Фигуры категорического силлогизма и их модусы.

3. Другие виды дедуктивных умозаключений.

1. Рассмотрение дедуктивных умозаключений принято начинать с особой, наиболее типичной для них формы, называемой простым категорическим силлогизмом. Это такое дедуктивное умозаключение, в котором из двух категорических суждений, связанных общим термином, выводится третье.

Структура силлогизма типична для всякого умозаключения: две посылки и заключение. Посылки и заключение содержат в себе термины:

а) меньший термин, представляющий собой субъект (S) заключения;

б) больший термин, представляющий собой предикат (P) заключения;

в) средний термин (М)[13], который входит в каждую посылку, но отсутствует в заключении; назначение его в том, чтобы быть связующим звеном между посылками силлогизма.

Названия «меньший» и «больший» для обозначения терминов силлогизма возникли потому, что предикат суждения, выступающего заключением, как правило, больше по объему, чем его субъект. Соответственно меньшей посылкой называется та, которая содержит меньший термин, а большей посылкой – та, которая содержит больший термин.

Рассмотрим сказанное на примере:

Большая посылка: Каждый гражданин России (M) имеет право на образование (P).

Меньшая посылка: В.И. Петров (S) – гражданин России (М).

Заключение: В.И. Петров (S) имеет право на образование (Р).

Здесь хорошо видно, что в заключении Р (имеющие право на образование) больше по объему, чем S (В.И. Петров). Средним термином (М), связывающим посылки и обеспечивающим возможность заключения, выступает понятие «гражданин России». Таким образом, общая схема силлогизма предстает в следующем виде:

М есть Р

S есть М

S есть P

При построении силлогизма важно следить не только за подбором посылок, позволяющих, благодаря наличию среднего термина, сделать правильный вывод. Не менее важно строго учитывать логическое осно­вание всякого силлогистического вывода, так называемую аксиому силлогизма: «Все, что утверждается (или отрицается) обо всем классе предметов, то распространяется и на любой предмет этого класса».

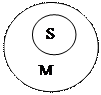
Аксиома силлогизма выражает связь понятий в силлогизме прежде всего по их содержанию. Но так как связь понятий по содержанию определяет и их соотношение по объемам, то аксиома силлогизма выражает также объемные отношения терминов силлогизма. На кругах Эйлера это можно изобразить так:

 

Р

Р Р

Схема 1. Схема 2

На схеме 1 показано, что если субъект силлогизма входит по объему в средний термин, а тот в свою очередь – в предикат силлогизма, то, следовательно, и субъект силлогизма входит в его предикат. На схеме 2. показано, что если средний термин силлогизма не входит ни одним своим элементом в предикат силлогизма, т.е. отрицается в нем, то и субъект данного силлогизма не может входить в его предикат. Рассмотрим сказанное на примерах:

 

Пример 1. Все жилые дома в нашем поселке (М) – кирпичные (Р).

Мой брат (S) имеет жилой дом в нашем поселке (М).

Мой брат (S) имеет кирпичный жилой дом (Р).

 

Пример 2. Никто из моих родных (М) не является юристом (Р).

С.М. Иванов (S) – мой родной дядя (М).

С.М. Иванов (S) не является юристом (Р).

 

Аксиома силлогизма не является единственным правилом, определяющим его построение. Существует еще целый ряд общих правил, без соблюдения которых невозможно правильно составить силлогизм и получить верное заключение. Все эти правила можно разбить на две группы: правила терминов и правила посылок. Начнем их рассмотрение с правил терминов.

Правило 1. В каждом силлогизме должно быть только три термина.

Это правило требует прежде всего однозначного употребления среднего термина в обеих посылках силлогизма. Дело в том, что зачастую в качестве среднего термина употребляются слова, могущие иметь (в зависимости от контекста) разные смысловые значения. Тогда возникает опасность совершения подмены понятий. Вот пример: из посылок «Труд – основа жизни» и «Изучение математики – труд» не следует, что изучение математики - основа жизни, так как понятие «труд» взято здесь в разных смыслах в каждой посылке (в первой – как философско-социологическая категория, включающая в себя все сущностные черты любого вида трудовой деятельности человека, а во второй – как частный вид умственной деятельности человека). Поэтому это понятие не может исполнить роль среднего термина. В результате произошла логическая ошибка, называемая учетверением терминов, и вывод оказался неверным.

Правило 2. Средний термин обязательно должен быть взят в полном объеме (распространен) хотя бы в одной из посылок. Нарушение этого правила ведет к тому, что средний термин перестает исполнять свою роль посредника (медиума) между большим и меньшим терминами. В результате вывод силлогизма теряет свою истинность.

Рассмотрим это на примере: «Все преподаватели вуза – доценты (М^–)»; «Некоторые доценты (М^–) – доктора наук»; из этого нельзя вывести, что все преподаватели вуза – доктора наук, поскольку здесь средний термин («доценты») не распространен ни в одной из посылок. Приведем другой пример: «Все доценты этой кафедры (М⁺) имеют ученую степень»; «Иван Петрович Сидоров - доцент этой кафедры (М^–)»; следовательно, «Иван Петрович Сидоров имеет ученую степень». Это верно построенный силлогизм, в котором средний термин («доценты кафедры») взят в полном объеме в первой посылке.

Правило 3. Термин, не взятый в полном объеме в посылках, не может быть взят во всем объеме и в заключении. Для пояснения этого правила приведем следующий пример: «Все преступники заслуживают наказания»; «Некоторые работники торговли – преступники». Отсюда никак не следует, что все работники торговли заслуживают наказания. Ошибка здесь в том, что термин «работники торговли», взятый в посылке не в полном объеме, мы в заключении распространяем на весь объем («все работники торговли»).

Теперь рассмотрим правила посылок:

Правило 4. Из двух частных посылок невозможно вывести никакого заключения. Это правило выводится из предыдущих. В самом деле, если обе посылки будут частными, то средний термин будет не распространен ни в одной из них, а значит будет нарушено правило 3. Например, из посылок «Некоторые работники фирмы – экономисты» и «Некоторые юристы – работники фирмы» никакого определенного вывода сделать нельзя, поскольку невозможно установить объемные отношения между терминами силлогизма. Объем субъекта («некоторые юристы») может перекрещиваться с объемом предиката («экономисты»), но может и вообще не иметь с ним общих элементов.

Правило 5. Если одна из посылок частная, то и заключение будет обязательно частным. Действительно, если мы желаем получить общее заключение в силлогизме, где одна из посылок частная, то нарушаются правила 2 либо 3. Например: «Все участники кросса – спортсмены»; «Некоторые студенты - участники кросса». Нельзя утверждать из сказанного, что все студенты - спортсмены. Нарушено правило 3, поэтому вывод неверен. Возьмем другой пример: «Некоторые врачи являются хирургами»; «Все терапевты является врачами». Вывод «Все терапевты являются хирургами» вновь оказывается ошибочен, так как нарушено правило 2.

Правило 6. Из двух отрицательных суждений невозможно сделать определенного вывода. В этом случае все термины исключают друг друга, никакую объемную взаимосвязь между ними установить невозможно. Соответственно никакого вывода сделать нельзя.

Правило 7. Если одна из посылок отрицательная, то и заключение будет отрицательным. Дело в том, что в этом случае отсутствует связь между средним термином (М) и одним из двух других терминов силлогизма (или S, или Р), что с необходимостью ведет к отрицанию либо субъекта, либо предиката заключительного суждения. Вот примеры:

1. Ни одна наука (М) не строится бессистемно (Р).

Биология (S) - наука (М).

Биология не строится бессистемно.

2. Все моржи (Р) относятся к ластоногим (М).

Это животное (S) не является ластоногим (М).

Это животное не является моржом.

 

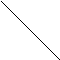
2. Как можно заметить, силлогизмы различаются между собой не толь­ко количественными и качественными характеристиками своих терминов, но и расположением в них средних терминов. В зависимости от этого в логике различают фигуры силлогизма. Их четыре. Схематично они выглядят следующим образом:

M Р P M M P P M

S М S M M S М S

Фигура 1 Фигура 2 Фигура 3 Фигура 4

В состав силлогизма могут входить разные по количественным и качественным показателям суждения: общеутвердительные (А), частноутвердительные (I), общеотрицательные (Е) и частноотрицательное (О). В зависимости от того или иного их сочетания получаются различные разновидности построения силлогизма, получившие в логике название модусов силлогизма. Всего существует 64 модуса, но при этом правильных модусов, т.е. таких, которые не противоречат правилам силлогизма и потому обеспечивают достоверность заключения (при условии, конечно, истинности посылок), всего 18. Приведем их для каждой фигуры:

1-я фигура2-я фигура3-я фигура4-я фигура

AAA АЕЕ ААI AAI

EAE ЕАЕ EAO EAO

AII АОО AII AEE

EIO EIO EIO IAI

IAI

OAO

Состав правильных модусов каждой фигуры определяют также ее особые правила. Так, в 1-й фигуре большая посылка должна быть всегда общей, а меньшая – утвердительной, во 2-й фигуре большая посылка также должна быть общей, но при этом одна из посылок – отрицательная, в 3-й фигуре меньшая посылка должна быть утвердительной, а заключение – частным. 4-я фигура весьма редко употребляется в практике нашего мышления, поэтому ее особые правила мы не рассматриваем.

В практике логических рассуждении мы далеко не всегда употребляем силлогизм в его полной форме. Полный силлогизм чаще всего применяется там, где требуется особая точность и доказательность аргументов (в математике, программировании и т.п.). Обычно же мы пользуемся силлогизмами в их сокращенной форме, когда одна из посылок, а иногда и заключение, не присутствуют в умозаключении в явной форме, а лишь подразумеваются. Такая форма силлогизма получила название энтимемы [14].

Например, если мы относительно кого-либо говорим: «Нужно быть злым человеком, чтобы делать подобные вещи», – то это выражение в форме полного силлогизма будет иметь вид: «Все люди, делающие подобные вещи, злые. Этот человек делает подобные вещи. Следовательно, этот человек злой».

Чаще всего в сокращенном силлогизме опускается большая посылка, так как обычно выражает широко известное положение. Но могут опускаться и меньшая посылка, и заключение.

Наряду с сокращенными силлогизмами мы зачастую пользуемся и сложными формами дедукции, получившими название полисиллогизмов. В таком умозаключении несколько простых силлогизмов соединяются между собой таким образом, что заключение одного из них становится посылкой для последующего. Различают прогрессивные и регрессивные полисиллогизмы.

В прогрессивном полисиллогизме заключение предшествующего простого категорического силлогизма становится большей посылкой последующего силлогизма. Пример такого полисиллогизма:

Все люди сильной воли (В) не боятся трудностей (А).

Все смелые люди (С) обладают сильной волей (В).

Все смелые люди (С) не боятся трудностей (А).

Все десантники (D) – смелые люди (С).

Следовательно, все десантники (D) не боятся трудностей (А).

Схема его такова: Все В суть А.

Все С суть В.

Все С суть А.

Все D суть C.

Следовательно, все D суть А.

В регрессивном полисиллогизме заключение предшествующего силлогизма становится меньшей посылкой последующего. Например:

Каждый организм (В) имеет тело (С).

Всякое растение (А) является организмом (В).

Любое тело (С) обладает весом (D).

Всякое растение (А) имеет тело (С).

Следовательно, все растения (А) обладают весом (D).

Схема при этом принимает вид: Все В суть С.

Все А суть В.

Все С суть D.

Все А суть С.

Следовательно, все А есть D

Отличают особый вид полисиллогизма – сорит [15], который состоит из сокращенных силлогизмов. В нем приводится лишь последнее заключение, остальные (промежуточные) – опускаются. Как и полисиллогизмы, сориты могут быть прогрессивными и регрессивными.

Прогрессивный сорит получается из прогрессивного полисиллогизма путем выбрасывания заключений предшествующих простых силлогизмов и больших посылок последующих. Он начинается с посылки, содержащей предикат заключения, и заканчивается посылкой, содержащей субъект заключения.

Пример такого сорита: «Все, что укрепляет здоровье (А), полезно (В). Занятия физкультурой (С) укрепляют здоровье (А). Легкая атлетика (D) – это физкультура (С). Бег (Е) – вид легкой атлетики (D). Следовательно, бег (Е) полезен (В)». Схема его: А – В; С – А; D – C; E – B, следовательно, А – D. Символизированная формула: 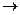(E - В).

Регрессивный сорит получается из регрессивного полисиллогизма путем выбрасывания заключений предшествующих простых силлогизмов и меньших посылок последующих. Он начинается с посылки, содержащей субъект заключения, и заканчивается посылкой, содержащей предикат заключения. Например: «Приобретающий острый ум (А), становится развитым человеком (В). Преодолевающий трудности (С), приобретает остроту ума (А). Вникающий в трудности научных проблем (D), способен их преодолевать (С). Привыкающий концентрировать свое внимание (Е), способен вникать в трудности научных проблем (D). Занимающийся наукой (F), привыкает концентрировать свое внимание (Е). Следовательно, занимающийся наукой (F), приобретает острый ум (А)». Схема сорита: А – В; С – А; D – С; Е – D; F – Е, следовательно,F – А. Символизированный вид: 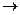(F – А).

Существуют также такие полисиллогизмы, посылками которых выступают энтимемы. Они в традиционной логике называются эпихейремами [16]. Пример эпихейремы: «Все, что не соответствует действительности (А) вызывает недоверие (В), а ложь (С) это утверждение, не соответствующее действительности (В). Лесть (D) есть ложь (С), поскольку она (D) сознательно искажает действительность (А). Следовательно, лесть (D) вызывает недоверие (В)».

3. Теперь можно перейти к рассмотрению других, указанных ранее, сложных ви­дов дедуктивных умозаключений. Как уже говорилось, в разделительно-категорическом умозаключении одна посылка – разделительное суждение, другая – категорическое суждение. Причем в категорическое суждение обязательно входят все, кроме одной, альтернативы разделительного суждения.

Разделительно-категорическое умозаключение имеет два модуса:

1) утверждающе – отрицающий;

2) отрицающе – утверждающий.

Общая схема первого из них: А есть или В, или С, или D; А есть С; следовательно, А не есть ни В, ни D. Важно подчеркнуть, что в этом модусе разделительная посылка должна быть обязательно суждением строгой дизъюнкции. Пример такого модуса: «Сергей сдавал вчера только один экзамен: или по химии, или по физике, или по истории. Сергей сдавал вчера экзамен по физике. Следовательно, Сергей не сдавал вчера экзамен ни по химии, ни по истории».

Символическая запись силлогизма приобретает вид: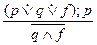

Общая схема второго модуса: А есть или В, или С, или D; А не есть ни В, ни С; следовательно, А есть D. Иначе говоря, такой модус позволяет путем отрицания неистинных альтернатив прийти к истинному выводу. В нем характер дизъюнкции (строгая или нестрогая) не влияет на истинность вывода. Однако обязательным условием достоверного вывода по этому модусу является полнота деления в разделительной посылке. Это значит, что в ней должны быть выделены все возможные альтернативы. В случае несоблюдения этого условия вывод будет лишь вероятностный. Пример: «Доцент П. может преподавать или философию, или этику, или эстетику. Доцент П. не преподает ни философию, ни эстетику. Следовательно, доцент П. преподает этику».

Символическая запись данного силлогизма имеет вид: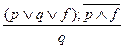

Условно-категорическое умозаключение (где из двух посадок одна – суждение условное, а другая – категорическое) также имеет два модуса. Первый модус утверждающий, второй – отрицающий.

В утверждающем модусе мысль идет от утверждения основания к утверждению следствия, по схеме: если есть А, то есть В; А есть; следовательно, есть и В. Пример: «Если я хорошо подготовлюсь, то сдам экзамен. Я хорошо подготовился. Следовательно, я сдам экза­мен».

Его символическая запись такова: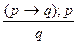

В отрицательном модусе мысль идет от отрицания следствия к от­рицанию основания по схеме: если есть А, то есть В; В нет; следовательно, нет и А. Пример: «Если вы хорошо подумаете, то найдете верное решение. Вы не нашли верного решения. Следовательно, вы не достаточно хорошо подумали».

В условно-категорическом умозаключении нельзя идти от отрицания основания к отрицанию следствия и от утверждения следствия к утверждению основания. Невозможно, к примеру, сделать вывод из таких посылок: «Если будет плохая погода, то мы не поедем на дачу. Погода сегодня хорошая». Дело в том, что, кроме указанной причины, может быть много других, в силу которых мы не сможет поехать на дачу: кто-то заболел, неожиданно пришли гости, не подошел автобус и т.д. Также невозможно сделать достоверный вывод из посылок: «Если автомашина исправна, то на ней можно ехать. Мы поехали на автомашине». Это, однако, не свидетельствует, что автомашина исправна, так как у нее могут быть неисправности, не препятствующие полностью тому, чтобы на ней можно было ездить, например, разбиты фары, или не отрегулирован как следует карбюратор и т.п. Исключение из этого правила составляют лишь такие умозаключения, а которых условная посылка имеет характер эквиваленции.

Могут быть и чисто условные умозаключения, в которых обе посылки являются ус­ловными суждениями. Их общая схема такая: Если есть А, то В; если есть В, то С; следовательно, если есть А, то есть и С. Например: «Если за мной заедут друзья, то мы поедем на озеро. Если мы поедем на озеро, то будем купаться. Следовательно, если за мной заедут друзья, то мы будем купаться».

Символическая запись чисто условного силлогизма: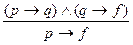

В условно-разделительном умозаключении одна посылка (большая) есть условное суждение, либо состоит из двух или более условных суждений, а другая посылка – разделительное суждение. Обычно такой вид умозаключения представляет собой дилемму, смысл которой в том, что выбор осуществляется всегда только между двумя альтернативами, поскольку третьего решения вопроса не существует.

Различают два основных модуса такого умозаключения – конструктивный и деструктивный. В конструктивном модусе заключение идет от утверждения основания к утверждению следствия. Причем из двух оснований вытекают два альтернативных следствия. Схема простой конструктивней дилеммы: Если А, то С; если В, то С; А либо В; следовательно, С. Пример: «Если удобрения улучшают структуру почвы, то повышается урожай. Если удобрения улучшают питание растений, то также повышается урожай. Но удобрения либо улучшают структуру почвы, либо улучшают питание растений. Следовательно, внесение удобрений повышает урожай».

Символический вид конструктивной дилеммы: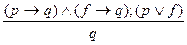

В деструктивной дилемме из одного основания вытекает два следствия, вторая посылка отрицает оба следствия, а вывод разрушает тем самым само основание. Таким образом, здесь заключение идет от отрицания следствия к отрицанию основания. Общая схема простой деструктивной дилеммы: Если А, то В; если А, то С; не – С; следовательно не – А. Пример: «Если предприятие выпускает качественную продукцию, то оно конкурентоспособно. Если предприятие выпускает качественную продукцию, то оно получает прибыль. Данное предприятие не конку­рентоспособно или не получает прибыль. Следовательно, предприятие не выпускает качественную продукцию».

Символическая запись деструктивной дилеммы: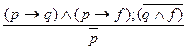

Не нашли, что искали? Воспользуйтесь поиском: