Векторная функция скалярного аргумента

z

A(x, y, z)

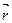
y

х

Пусть некоторая кривая в пространстве задана параметрически:

x = j(t); y = y(t); z = f(t);

Радиус- вектор произвольной точки кривой: .

Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора .

Запишем соотношения для некоторой точки t₀:

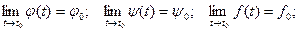
Тогда вектор - предел функции (t). .

Очевидно, что

, тогда

.

Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.

; ;

или, если существуют производные j¢(t), y¢(t), f¢(t), то

Это выражение – вектор производная вектора .

Если имеется уравнение кривой:

x = j(t); y = y(t); z = f(t);

то в произвольной точке кривой А(x_А, y_А, z_А) с радиус- вектором

можно провести прямую с уравнением

Т.к. производная - вектор, направленный по касательной к кривой, то

.

Уравнение нормальной плоскости к кривой будет иметь вид:

Пример. Составить уравнения касательной и нормальной плоскости к линии, заданной уравнением в точке t = p/2.

Уравнения, описывающие кривую, по осям координат имеют вид:

x(t) = cost; y(t) = sint; z(t) = ;

Находим значения функций и их производных в заданной точке:

x¢(t) = -sint; y¢(t) = cost;

x¢(p/2) = -1; y¢(p/2) = 0; z¢(p/2)=

x(p/2) = 0; y(p/2) = 1; z(p/2)= p /2

- это уравнение касательной.

Нормальная плоскость имеет уравнение:

Не нашли, что искали? Воспользуйтесь поиском: