Параметрическое задание функции

Исследование и построение графика кривой, которая задана системой уравнений вида:

,

производится в общем то аналогично исследованию функции вида y = f(x).

Находим производные:

Теперь можно найти производную 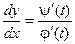. Далее находятся значения параметра t, при которых хотя бы одна из производных j¢(t) или y¢(t) равна нулю или не существует. Такие значения параметра t называются критическими.

Для каждого интервала (t₁, t₂), (t₂, t₃), …, (t_k-1, t_k) находим соответствующий интервал (x₁, x₂), (x₂, x₃), …, (x_k-1, x_k) и определяем знак производной на каждом из полученных интервалов, тем самым определяя промежутки возрастания и убывания функции.

Далее находим вторую производную функции на каждом из интервалов и, определяя ее знак, находим направление выпуклости кривой в каждой точке.

Для нахождения асимптот находим такие значения t, при приближении к которым или х или у стремится к бесконечности, и такие значения t, при приближении к которым и х и у стремится к бесконечности.

В остальном исследование производится аналогичным также, как и исследование функции, заданной непосредственно.

На практике исследование параметрически заданных функций осуществляется, например, при нахождении траектории движущегося объекта, где роль параметра t выполняет время.

Ниже рассмотрим подробнее некоторые широко известные типы параметрически заданных кривых.

Не нашли, что искали? Воспользуйтесь поиском: