Несобственные интегралы. Пусть функция f(x) определена и непрерывна на интервале [a, ¥)

Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).

Обозначение: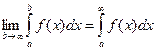

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

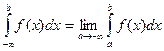
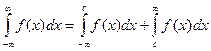
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Пример.

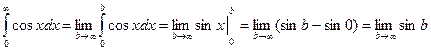- не существует.

Несобственный интеграл расходится.

Пример.

- интеграл сходится

Теорема: Если для всех х (x ³ a) выполняется условие и интеграл сходится, то тоже сходится и ³ .

Теорема: Если для всех х (x ³ a) выполняется условие и интеграл расходится, то тоже расходится.

Теорема: Если 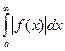сходится, то сходится и интеграл .

В этом случае интеграл называется абсолютно сходящимся.

Не нашли, что искали? Воспользуйтесь поиском: