Способ. Метод неопределенных коэффициентов.

Рассмотрим интегралы следующих трех типов:

где P(x) – многочлен, n – натуральное число.

Причем интегралы II и III типов могут быть легко приведены к виду интеграла I типа.

Далее делается следующее преобразование:

в этом выражении Q(x)- некоторый многочлен, степень которого ниже степени многочлена P(x), а l - некоторая постоянная величина.

Для нахождения неопределенных коэффициентов многочлена Q(x), степень которого ниже степени многочлена P(x), дифференцируют обе части полученного выражения, затем умножают на и, сравнивая коэффициенты при одинаковых степенях х, определяют l и коэффициенты многочлена Q(x).

Данный метод выгодно применять, если степень многочлена Р(х) больше единицы. В противном случае можно успешно использовать методы интегрирования рациональных дробей, рассмотренные выше, т.к. линейная функция является производной подкоренного выражения.

Пример.

.

Теперь продифференцируем полученное выражение, умножим на и сгруппируем коэффициенты при одинаковых степенях х.

=

=

Итого =

=

Пример.

Пример.

Второй способ решения того же самого примера.

С учетом того, что функции arcsin и arccos связаны соотношением , а постоянная интегрирования С – произвольное число, ответы, полученные различными методами, совпадают.

Как видно, при интегрировании иррациональных функций возможно применять различные рассмотренные выше приемы. Выбор метода интегрирования обуславливается в основном наибольшим удобством, очевидностью применения того или иного метода, а также сложностью вычислений и преобразований.

Пример.

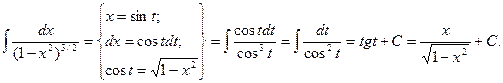
Несколько примеров интегралов, не выражающихся через

элементарные функции

К таким интегралам относится интеграл вида , где Р(х)- многочлен степени выше второй. Эти интегралы называются эллиптическими.

Если степень многочлена Р(х) выше четвертой, то интеграл называется ультраэллиптическим.

Если все – таки интеграл такого вида выражается через элементарные функции, то он называется псевдоэллиптическим.

Не могут быть выражены через элементарные функции следующие интегралы:

1) - интеграл Пуассона (Симеон Дени Пуассон – французский математик (1781-1840))

2) - интегралы Френеля (Жан Огюстен Френель – французский ученый (1788-1827) - теория волновой оптики и др.)

3) - интегральный логарифм

4) - приводится к интегральному логарифму

5) - интегральный синус

6) 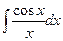- интегральный косинус

Не нашли, что искали? Воспользуйтесь поиском: