Интегрирование некоторых иррациональных функций

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Интеграл вида где n- натуральное число.

С помощью подстановки функция рационализируется.

Тогда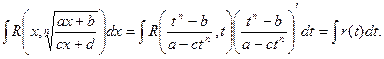

Пример.

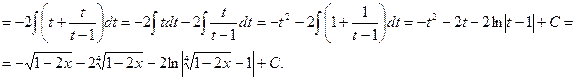
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

Пример.

Интегрирование биноминальных дифференциалов

Определение: Биноминальным дифференциалом называется выражение

x^m(a + bxⁿ)^pdx

где m, n, и p – рациональные числа.

Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:

1) Если р – целое число, то интеграл рационализируется с помощью подстановки

, где l - общий знаменатель m и n.

2) Если - целое число, то интеграл рационализируется подстановкой

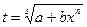, где s – знаменатель числа р.

3) Если - целое число, то используется подстановка 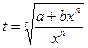, где s – знаменатель числа р.

Интегралы вида

Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.

Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:

Таким образом, интеграл приводится к одному из трех типов:

1)

2)

3)

Не нашли, что искали? Воспользуйтесь поиском: