Интегрирование некоторых тригонометрических

Функций

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Пример.

Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Пример.

Интеграл вида если

функция R является нечетной относительно cosx

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.

Функция может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.

Пример.

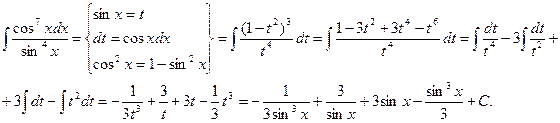
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

Интеграл вида если

функция R является нечетной относительно sinx

По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

Пример.

Интеграл вида

функция R четная относительно sinx и cosx

Для преобразования функции R в рациональную используется подстановка

t = tgx.

Тогда

Пример.

Интеграл произведения синусов и косинусов

различных аргументов

В зависимости от типа произведения применятся одна из трех формул:

Пример.

Пример.

Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.

Пример.

Пример.

Иногда применяются некоторые нестандартные приемы.

Пример.

Итого

Не нашли, что искали? Воспользуйтесь поиском: