ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Описанная окружность
Треугольник
27892. Сторона правильного треугольника равна 
. Найдите радиус окружности, описанной около этого треугольника.
27893. Радиус окружности, описанной около правильного треугольника, равен . Найдите сторону этого треугольника.
27894. Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.
27895. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
27900. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен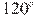 
. Найдите диаметр описанной окружности этого треугольника.
27923. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
27918. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен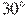 
. Найдите радиус окружности, описанной около этого треугольника.
27919. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
27922. Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
27920. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 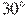. Найдите сторону AB этого треугольника.
27921. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 
. Найдите радиус окружности, описанной около этого треугольника.
27896. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.
27897. Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника.
27898. В треугольнике ABC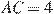 
, 
, угол C равен 
. Найдите радиус описанной окружности этого треугольника.
Трапеция
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найти высоту трапеции.
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Четырехугольник
27927. Два угла вписанного в окружность четырехугольника равны 
и 
. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Шестиугольник
27929. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
27906. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Многоугольник
27930. Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 
. Найдите число вершин многоугольника.
Не нашли, что искали? Воспользуйтесь поиском: