
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задания для контрольной работы № 2
Задание № 6
Даны комплексные числа z 1 и z 2 (таблица 5).
а). Записать их в тригонометрической форме и отметить полученные числа на комплексной плоскости; б). Найти числа z 1 + z 2, z 1 – z 2, построить; в). Найти z 1 z 2, z 1 / z 2, записать в тригонометрической и алгебраической формах, сравнить результаты; г). Найти 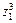 ; д). Найти
; д). Найти  , построить.
, построить.
Таблица 5
| № варианта | z 1 | z 2 | № варианта | z 1 | z 2 |
| 6.1. | 
| 
| 6.16. | 
| 
|
| 6.2. | 3 + 3 i | 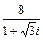
| 6.17 | – 4 + 4 i | 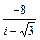
|
| 6.3. | 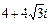
| 
| 6.18. | 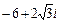
| 
|
| 6.4. | 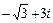
| 
| 6.19. | 
| 
|
| 6.5. | – 2 + 2 i | 
| 6.20. | 3 – 3 i | 
|
| 6.6. | 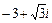
| 
| 6.21. | 
| 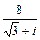
|
| 6.7 | 
| 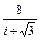
| 6.22. | 
| 
|
| 6.8. | – 4 – 4 i | 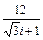
| 6.23. | 2 – 2 i | 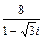
|
| 6.9. | 
| 
| 6.24. | 
| 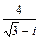
|
| 6.10. | 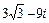
| 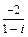
| 6.25. | 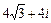
| 
|
| 6.11. | 1 – i | 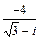
| 6.26. | 1 + i | 
|
| 6.12. | 
| 
| 6.27 | 
| 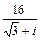
|
| 6.13. | 
| 
| 6.28. | 
| 
|
| 6.14. | 2 + 2 i | 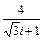
| 6.29. | – 5 + 5 i | 
|
| 6.15. | 
| 
| 6.30. | 
| 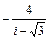
|
Задание № 7
Найти пределы функций.
7.1. а) 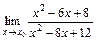 при
при  ,
, 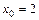 ,
,  ;
;
б) 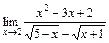 ; в)
; в) 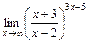 ; г)
; г)  .
.
7.2. а)  при
при 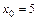 ,
,  ,
,  ;
;
б) 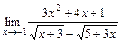 ; в)
; в) 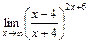 ; г)
; г)  .
.
7.3. а) 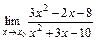 при
при 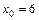 ,
, 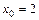 ,
,  ;
;
б) 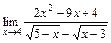 ; в)
; в)  ; г)
; г) 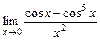 .
.
7.4. а)  при
при  ,
, 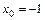 ,
,  ;
;
б) 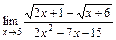 ; в)
; в) 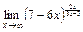 ; г)
; г)  .
.
7.5. а)  при
при 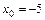 ,
,  ,
,  ;
;
б) 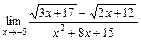 ; в)
; в)  ; г)
; г) 
7.6. а)  при
при  ,
, 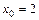 ,
,  ;
;
б)  ; в)
; в)  ; г)
; г)  .
.
7.7. а)  при
при 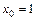 ,
,  ,
,  ;
;
б) 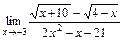 ; в)
; в)  ; г)
; г) 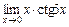 .
.
7.8. а)  при
при  ,
, 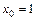 ,
,  ;
;
б)  ; в)
; в)  ; г)
; г) 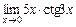 .
.
7.9. а)  при
при  ,
,  ,
,  ;
;
б)  ; в)
; в) 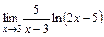 ; г)
; г)  .
.
7.10. а) 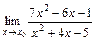 при
при  ,
, 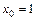 ,
,  ;
;
б)  ; в)
; в)  ; г)
; г) 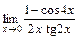 .
.
7.11. а) 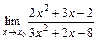 при
при  ;
;
б) 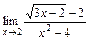 ; в)
; в) 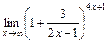 ; г)
; г)  .
.
7.12. а) 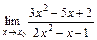 при
при  ;
;
б) 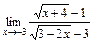 ; в)
; в) 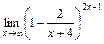 ; г)
; г)  .
.
7.13. а) 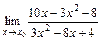 при
при  ;
;
б) 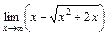 ; в)
; в)  ; г)
; г)  .
.
7.14. а)  при
при 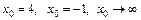 ;
;
б)  ; в)
; в) 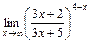 ; г)
; г) 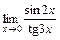 .
.
7.15. а) 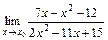 при
при  ;
;
б)  ; в)
; в)  ; г)
; г)  .
.
7.16. а) 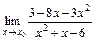 при
при  ;
;
б)  ; в)
; в) 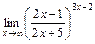 ; г)
; г) 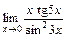 .
.
7.17. а)  при
при 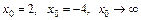 ;
;
б) 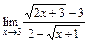 ; в)
; в)  ; г)
; г) 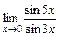 .
.
7.18. а)  при
при 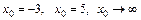 ;
;
б) 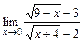 ; в)
; в)  ; г)
; г) 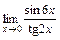 .
.
7.19. а)  при
при 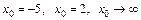 ;
;
б)  ; в)
; в)  ; г)
; г) 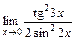 .
.
7.20. а) 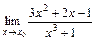 при
при 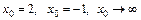 ;
;
б)  ; в)
; в)  ; г)
; г) 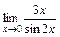 .
.
7.21. а)  при
при  2,
2,  3,
3,  ;
;
б) 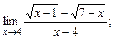 в)
в) 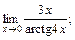

7.22. а)  при
при  0,
0,  2,
2,  ;
;
б)  в)
в) 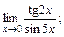

7.23. а)  при
при  3,
3,  –3,
–3,  ;
;
б) 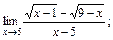 в)
в) 

7.24. а)  при
при  –3,
–3,  –2,
–2,  ;
;
б) 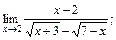 в)
в) 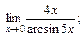

7.25. а)  при
при  2,
2,  4,
4,  ;
;
б) 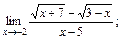 в)
в) 

7.26. а) 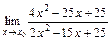 при
при  2,
2,  5,
5,  ;
;
б)  в)
в) 
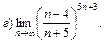
7.27. а)  при
при  1,
1,  –4,
–4,  ;
;
б) 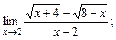 в)
в) 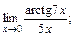
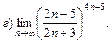
7.28. а) 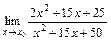 при
при  5,
5,  –5,
–5,  ;
;
б)  в)
в) 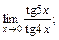
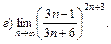
7.29. а)  при
при  –2,
–2,  1,
1,  ;
;
б)  в)
в) 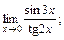

7.30. а)  при
при  –2,
–2,  –1,
–1,  ;
;
б) 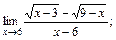 в)
в) 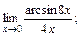
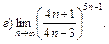
Задание № 8
Задана функция y = f (x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
| 8.1. | 
| 8.16. | 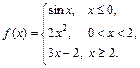
|
| 8.2. | 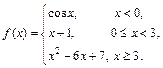
| 8.17. | 
|
| 8.3. | 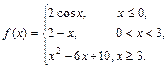
| 8.18. | 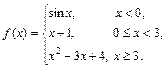
|
| 8.4. | 
| 8.19. | 
|
| 8.5. | 
| 8.20. | 
|
| 8.6. | 
| 8.21. | 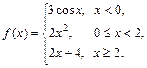
|
| 8.7. | 
| 8.22. | 
|
| 8.8. | 
| 8.23. | 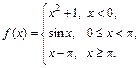
|
| 8.9. | 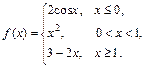
| 8.24. | 
|
| 8.10. | 
| 8.25. | 
|
| 8.11. | 
| 8.26. | 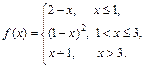
|
| 8.12. | 
| 8.27. | 
|
| 8.13. | 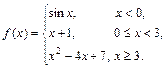
| 8.28. | 
|
| 8.14. | 
| 8.29. | 
|
| 8.15. | 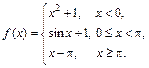
| 8.30. | 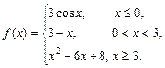
|
Задание № 9
Дано уравнение f (x) = 0. Требуется: 1) графическим методом отделить корень этого уравнения; 2) найти этот корень с точностью до 0,1 методом деления отрезка пополам.
| 9.1. | 2 x + 5 x = 0. | 9.2. | х 3 + 2 х – 7 = 0 | 9.3. | х – (х + 1)3 = 0. |
| 9.4. | ln x + 5 x = 0. | 9.5. | x ln x – 4 = 0. | 9.6. | х 3 + 3 х – 7 = 0. |
| 9.7. | ln x – 6 + 7 x = 0. | 9.8. | 3 x + 4 x = 0. | 9.9. | 4 x + 2 x = 0. |
| 9.10. | 5 x + 3 x = 0. | 9.11. | 2 x + 2 x – 2 = 0. | 9.12. | ln x + 3 x – 2 = 0. |
| 9.13. | 2 х + 5 х – 3 = 0. | 9.14. | ln x + 3 x – 1 = 0. | 9.15. | x ln x – 5 = 0. |
| 9.16. | 2 ex – x 2 = 0. | 9.17. | ln x – 5 + 6 x = 0. | 9.18. | 4 x + 5 x = 0. |
| 9.19. | ex + 3 x = 0. | 9.20. | 4 x + 3 x = 0. | 9.21. | ex + 5 x = 0. |
| 9.22. | 3 x 2 – 7 ex = 0. | 9.23. | 3 x + x = 0. | 9.24. | 2 ln x + 5 x = 0. |
| 9.25. | 3 x ln x – 7 = 0. | 9.26. | х 3 + 4 х + 1 = 0. | 9.27. | ln x – 7 + 8 x = 0. |
| 9.28. | 2×3 x + 7 x = 0. | 9.29. | 3×4 x + 7 x = 0. | 9.30. | 2×5 x + 7 x = 0. |
Решение типового варианта КР № 2
2 Задание 6. Даны комплексные числа z 1  и z 2
и z 2 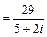 . а). Записать их в тригонометрической форме и отметить полученные числа на комплексной плоскости; б). Найти числа z 1 + z 2, z 1 – z 2, построить; в). Найти z 1 z 2, z 1 / z 2, записать в тригонометрической и алгебраической формах, сравнить результаты; г). Найти
. а). Записать их в тригонометрической форме и отметить полученные числа на комплексной плоскости; б). Найти числа z 1 + z 2, z 1 – z 2, построить; в). Найти z 1 z 2, z 1 / z 2, записать в тригонометрической и алгебраической формах, сравнить результаты; г). Найти 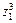 ; д). Найти
; д). Найти  , построить.
, построить.
Решение. а). Преобразуем число 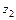 к виду
к виду 
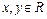 , для этого умножим и разделим его на число, сопряженное к знаменателю
, для этого умножим и разделим его на число, сопряженное к знаменателю
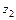
 .
.
Запишем числа 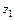 и
и 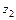 в тригонометрической форме. Воспользуемся формулами
в тригонометрической форме. Воспользуемся формулами
 ,
, 

 ,
, 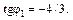
Точка 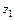 попадает во вторую четверть, поэтому j1 = arctg (–4 / 3) + 180° = = –53,13° + 180° = 126,87° Þ
попадает во вторую четверть, поэтому j1 = arctg (–4 / 3) + 180° = = –53,13° + 180° = 126,87° Þ 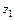
 = 5
= 5 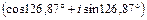 .
.
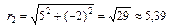 ,
, 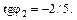
Точка 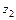 попадает в четвертую четверть, поэтому j2 = arctg (–2 / 5) = –21,8° и
попадает в четвертую четверть, поэтому j2 = arctg (–2 / 5) = –21,8° и
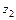
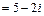 = 5,39
= 5,39  .
.
 |
Отметим полученные числа на комплексной плоскости (рисунок 4).
б). Вычислим z 3 = z 1 + z 2, z 4 = z 1 – z 2. В алгебраической форме
z 3 = 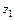 +
+ 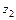

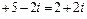 ;
;
z 4 = 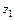 –
– 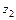

 .
.
Отметим полученные числа на комплексной плоскости (рисунок 9.1).
в). Вычислим z 1 z 2 и z 1 / z 2.
В алгебраической форме
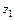
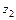
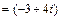
 ;
;

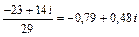 ;
;
в тригонометрической форме по формулам


имеем
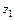
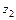 = 5
= 5 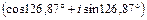 5,39
5,39  =
=
= 26,95  ,
,
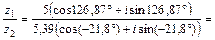
 .
.
Для проверки полученных результатов перейдем от тригонометрической формы записи комлексных чисел опять к алгебраической:
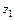
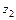 = 26,95
= 26,95  = 26,95 (–0,26 + 0,966 i) = –7,01 + 26,02 i,
= 26,95 (–0,26 + 0,966 i) = –7,01 + 26,02 i,
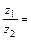
 = 0,93 (–0,854 + 0,52 i) = –0,79 + 0,48 i.
= 0,93 (–0,854 + 0,52 i) = –0,79 + 0,48 i.
Таким образом, расчеты выполнены верно.
в) Вычислим 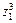 . По формуле
. По формуле 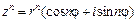 имеем
имеем
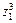 = 53
= 53 
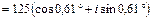 .
.
Для нахождения корней третьей степени воспользуемся формулой Муавра  :
:
 Þ
Þ

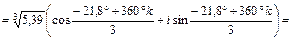
 ,
, 


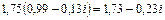 ;
;
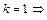

 ;
;
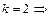

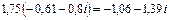 .
.
Отметим полученные числа на комплексной плоскости (рисунок 4).
2Задание 7. Вычислить пределы
а) 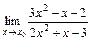 при х 0 = 2; х 0 = 1; х 0 ® ¥.
при х 0 = 2; х 0 = 1; х 0 ® ¥.
б)  ; в)
; в)  ; г)
; г)  .
.
Решение. При вычислении пределов допустимы использование уже известных пределов и элементарные преобразования. В некоторых случаях бывает целесообразным использовать для приближенных вычислений при малых значениях х (всюду 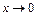 ) таблицу эквивалентных бесконечно малых:
) таблицу эквивалентных бесконечно малых:
1) 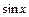 ~ х, ~ х,
| 2) tg x ~ х, | 3) 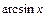 ~ х, ~ х,
|
4) 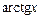 ~ х, ~ х,
| 5)  ~ ~  , ,
| 6) 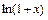 ~ х, ~ х,
|
7) 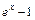 ~ х, ~ х,
| 8)  ~ х ln a, ~ х ln a,
| 9)  ~ aх. ~ aх.
|
а) 1. 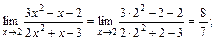
а) 2. 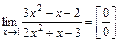 .
.
Неопределенности вида 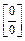 раскрываются путем сокращения на множитель, дающий 0. Разложим числитель и знаменатель на множители по формуле
раскрываются путем сокращения на множитель, дающий 0. Разложим числитель и знаменатель на множители по формуле  . Для этого решим уравнения
. Для этого решим уравнения  и
и  . Корни первого уравнения – {1, –2 / 3}, второго – {1, –3 / 2}, тогда
. Корни первого уравнения – {1, –2 / 3}, второго – {1, –3 / 2}, тогда
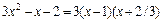 ,
, 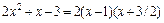 .
.
Подставим полученные разложения под знак предела и получим
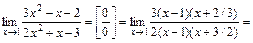
 .
.
а) 3.  .
.
Такие неопределенности раскрываются путем вынесения старшей степени неизвестной
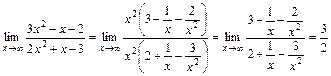 .
.
б)  .
.
Для того, чтобы избавиться от иррациональностей, умножим и числитель и знаменатель на выражение, сопряженное числителю:


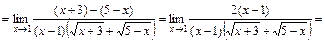
 .
.
в) 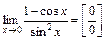 .
.
Для раскрытия неопределенностей такого вида воспользуемся первым замечательным пределом  и равенством
и равенством  .
.
Тогда

 .
.
г)  .
.
Для раскрытия неопределенностей вида  воспользуемся вторым замечательным пределом
воспользуемся вторым замечательным пределом 
Тогда
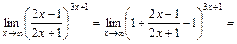
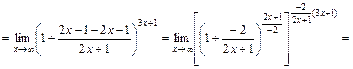
 . v
. v
2 Задание 8. Задана функция 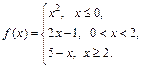 Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
Решение. В интервалах (–¥; 0), (0, 2) и (2, ¥) функция непрерывна. Исследуем функцию на непрерывность в точках х 1 = 0 и х 2 = 2. Воспользуемся условием непрерывности функции в точке х 0  .
.
1) исследуем точку х 1 = 0:


точка х 1 = 0 – точка разрыва функции 1 рода со cкачком s (0) = –1;
2) исследуем точку х 2 = 2:
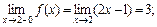
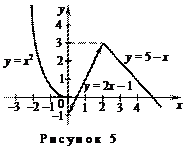
 ,
,
следовательно, в точке х 2 = 2 функция непрерывна. Построим график (см. рисунок 5). v
2 Задание 9. Дано уравнение  . Требуется: 1) Графическим методом отделить корень этого уравнения. 2) Найти этот корень методом половинного деления с точностью e = 0,1.
. Требуется: 1) Графическим методом отделить корень этого уравнения. 2) Найти этот корень методом половинного деления с точностью e = 0,1.
Решение. Для нашего примера примем 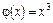 ;
;  .
.
Графики этих функций изображены на рисунке 6.
Как видно,  . Рассмотрим отрезок [0, 1]. Имеем
. Рассмотрим отрезок [0, 1]. Имеем
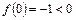 ;
;  ;
; 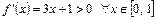 .
.
Таким образом, на отрезке [0, 1] функция f (x) непрерывна, принимает значения разных знаков на концах отрезка [0, 1] и первая производная  сохраняет знак на интервале (0, 1), поэтому на этом отрезке имеется единственный корень. Рассмотрим интервалы
сохраняет знак на интервале (0, 1), поэтому на этом отрезке имеется единственный корень. Рассмотрим интервалы  и
и  :
:
 ,
,
т. е. на этих интервалах функция f (x) не меняет знак, следовательно, корней на них нет.
Найдем корень на отрезке [0, 1]. Итерационная процедура метода половинного деления будет иметь вид
1)  ,
, 
 < 0;
< 0;
2) 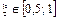 ,
, 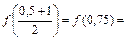 0,753 + 0,75 – 1 = 0,172 > 0;
0,753 + 0,75 – 1 = 0,172 > 0;
3) 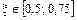 ,
, 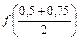 = f (0,625) = 0,6253 + 0,625 – 1 = –0,131 < 0;
= f (0,625) = 0,6253 + 0,625 – 1 = –0,131 < 0;
4)  ,
,  =
=
f (0,688) = 0,6883 + 0,688 – 1 = 0,012 > 0;
 5) x Î [0,625; 0,688].
5) x Î [0,625; 0,688].
Так как длина последнего отрезка 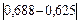 = 0,063 < e = 0,1, то процесс закончен и приближенное значение корня
= 0,063 < e = 0,1, то процесс закончен и приближенное значение корня 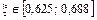 . Возьмем в качестве корня середину отрезка, т. е.
. Возьмем в качестве корня середину отрезка, т. е.  0,66.
0,66.
Для проверки результатов расчетов вычислим f (0,66): 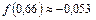 , т. е. корень найден верно. v
, т. е. корень найден верно. v
¨ Рекомендуемая литература
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 2004. 376 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. для втузов. В 2-х томах. Т. I. М.: Интеграл-пресс, 2007. 416 с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 1. М.: Высшая школа, 2007. 416 с.
4. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономических специальностей: Учебник и практикум. Ч. 1. Под ред. Кремера Н.Ш. М.: Высшее образование, 2005. 486 с.
5. Письменный Д.Т. Конспект лекций по высшей математике (часть 1). М.: Айрис-пресс, 2004. 288 с.
6. Высшая математика: Методические указания, рабочая программа и контрольные задания для студентов заочной формы обучения инженерно-технических специальностей. Часть 1 / Ю.В. Гуменникова, Л.В. Кайдалова, О.Е. Лаврусь; Самара: СамГУПС, 2009. 72 с. (МУ № 2298).
7. Высшая математика. Тренировочные тестыдля студентов заочной формы обучения инженерно-технических и экономических специальностей (1 семестр) / А.Д. Бочкарев, Л.В. Кайдалова; Самара: СамГУПС, 2009. 34 с. (МУ № 2253).
8. Климова Е.Н., Маркович О.Ф. Элементы линейной алгебры и аналитической геометрии. Конспект лекций для студентов первого курса всех специальностей и форм обучения. Самара: СамГАПС, 2003. 64 с.
9. Высшая математика. Тренировочные тестыдля студентов инженерно-технических и экономических специальностей / А.П. Зубарев, Л.В. Кайдалова; Самара: СамГАПС, 2005. 28 с. (МУ № 1579).
Оглавление
1. Задания для контрольной работы №1.............................................................................. 3
Задание № 1...................................................................................................................... 3
Задание № 2...................................................................................................................... 4
Задание № 3...................................................................................................................... 6
Задание № 4...................................................................................................................... 7
Задание № 5...................................................................................................................... 8
2. Решение типового варианта КР № 1................................................................................. 8
3. Задания для контрольной работы № 2........................................................................... 18
Задание № 6.................................................................................................................... 18
Задание № 7.................................................................................................................... 19
Задание № 8.................................................................................................................... 23
Задание № 9.................................................................................................................... 25
4. Решение типового варианта КР № 2............................................................................... 25
Рекомендуемая литература........................................................................................... 31
План 2009 г.
Не нашли, что искали? Воспользуйтесь поиском: