Пояснения к лабораторной работе №3_4 Задание 6

Задание:

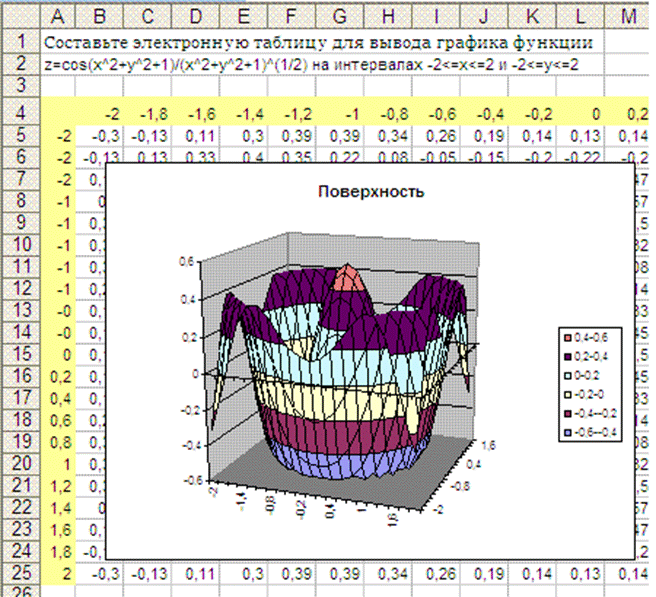
Составьте электронную таблицу для вывода графика функции z=cos(x^2+y^2+1)/(x^2+y^2+1)^(1/2) на интервалах -2<=x<=2 и -2<=y<=2

Выполнение. Следует учесть, что независимых переменных в данном случае две (x и y), в отличие от ранее рассмотренных случаев графиков на плоскости. Соответственно, для построения графика надо рассмотреть все варианты изменения каждой из них в заданном интервале от -2 до 2, ( важно: переменные меняются независимо друг от друга, т.е. если шаг для каждой будет равен 0,2 то, соответственно, на заданных интервалах будет 20 значений x и 20 значений y, а для z будет необходимо найти 20×20 = 400 значений).

В первых двух строках листа запишем пояснение – формулировку задания.

В 4 -ой строке начиная со столбца B запишем значения независимой переменной x на интервале от -2 до 2, задав

• - начальное значение -2 (в ячейке В4),
• - второе значение, отстоящее от первого на величину шага 0,2 и -1,8 (в ячейке C4)

и затем выделим обе ячейки и с использованием маркера автозаполнения заполним соответствующими значениями x диапазон B4:V4.

В ячейке A5 запишем первое значение независимой переменной y равное -2, в ячейке A6 – второе значение -1,8, и затем заполним диапазон A5:A25 последовательными значениями y.

Особое внимание следует обратить на пригодный для копирования ввод формулы для вычисления независимой переменной z. Записать формулу для первого, соответствующего x=-2 и y=-2 значения z (в ячейке B5) следует так, чтобы при копировании в ячейки справа и снизу от B5 сохранялись бы ссылки на строку 4 (в которой размещены значения x) и на столбец A ( в котором размещены значения y).

Для этого в формуле для z (в ячейке B5), ссылающейся на ячейки B4 (первое значение x) и A5 ( первое значение y ) будем использовать смешанные ссылки ( то есть такие, у которых абсолютной, не меняющейся при копировании будет только ссылка на номер строки или только ссылка на номер столбца, например B$4 или $A5, а вторая часть ссылки будет относительной, то есть меняющейся при копировании ).

Справка. Пусть

- в С3 введена формула =A1 (то есть относительная ссылка ),

- в D3 – формула =A$1, (то есть смешанная ссылка – относительная ссылка на столбец A и абсолютная – на строку 1 )

- в E3 - формула =$A1 (то есть смешанная ссылка – абсолютная ссылка на столбец A и относительная – на строку 1 )

- в F3 - формула =$A$1 (то есть абсолютная ссылка )

Тогда при копировании четырех ячеек диапазона C3:F3 в диапазон D4:G4 ( на одну строку ниже и на один столбец правее ) в ячейках будут размещены ссылки:

- в D4 - формула = B2 (то есть ссылка на ячейку также на одну строку ниже и на один столбец правее ),

- в E4 – формула =B$1, (то ссылка на ячейку, размещенную на один столбец правее но в той же, что и ранее строке 1 т.к ссылка на строку 1 абсолютная и не меняется при копировании)

- в F4 - формула =$A2 (то ссылка на ячейку, размещенную на одну строку ниже но в том же столбце A, поскольку ссылка на столбец A абсолютная и не меняется при копировании)

- в G3 - формула =$A$1 (то есть ссылка на ту же, что и ранее ячейку A1 поскольку ссылка абсолютная и не меняется при копировании)

Соответственно, записаная для z(-2,-2) в ячейке B5 формула будет иметь вид:

=COS(B$4^2+$A5^2+1)/(B$4^2+$A5^2+1)^(1/2)

Эту формулу следует скопировать в ячейку С6 и убедиться в том, что сохранились ссылки на 4 строку (х) и на столбец A ( y ).

После копирования данной формулы в диапазон B5:V25 следует выделить диапазон A4:V25 и вызвать Мастер построения диаграмм, выбрать Тип диаграммы Поверхность и задать заголовок диаграммы (например, Диаграмма поверхности), после чего будет построена такая диаграмма:

Не нашли, что искали? Воспользуйтесь поиском: