
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Координатный способ задания движения точки
Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i, j, k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, коорди 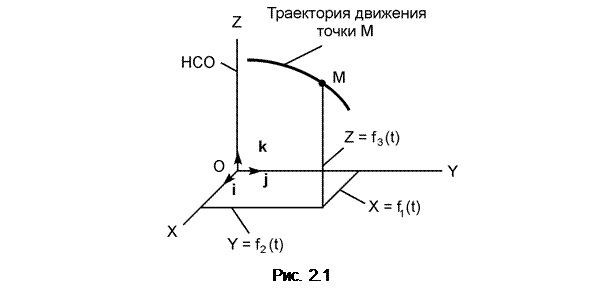
наты X, Y, Z движущейся точки М являются функциями времени t.
Систему трёх уравнений X = f1(t); Y = f2(t); Z = f3(t) называют уравнениями движения точки в пространстве в декартовых координатах.
Пример: X = 10·t2 + 1; Y = 7·t3 + t2 + 1; Z = 10·sin(p·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.
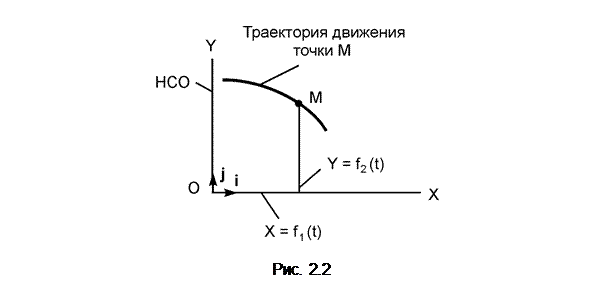
Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f1(t); Y = f2(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.
Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t2 + t2 + t; Y = 7·cos(p·t).
Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).
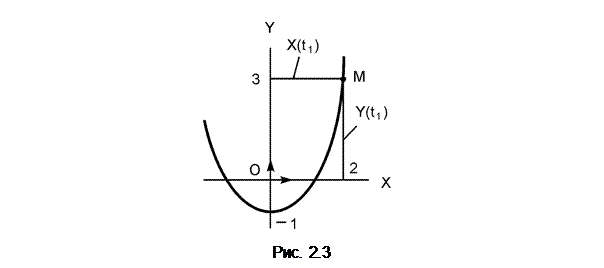
Пример. Заданы уравнения: X = 4·t (см); Y = 16·t2 – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t1 = 0,5 с.
Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t2 – 1. Получаем
Y = 16·(X/4)2 – 1 = X2 – 1.
Выражение Y = X2 – 1 есть уравнение параболы (y= a·x2+b·x+c) с вершиной в точке с координатами (0, – 1). В момент времени t1 = 0,5 с определяем координаты:
X(t1) = 4·t1 = 4·0,5 = 2 см > 0;
Y(t1) = 16·(t1)2 – 1 = 16·(0,5)2 – 1 = 3 см >0.
Показываем положение точки на траектории её движения (рис. 2.3).
Пример. Дано: X = 3·sin(p·t), см (1); Y = 3·cos(p·t), см (2); t1 = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t1.
Решение. Уравнения движения точки представим в следующем виде: (X)2 = (3·sin(p·t))2 (1I); (Y)2 = (3·cos(p·t))2 (2I). Для решения используем тригонометрическую формулу sin2(α) + cos2(α) = 1.
Складывая левые и правые части уравнений (1I) и (2I), получим (X)2 + (Y)2 = 32·(sin2(p·t) + cos2(p·t)) = 32·1 или (X)2 + (Y)2 = 32. Известно, что уравнение (X)2 + (Y)2 = R2 есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка 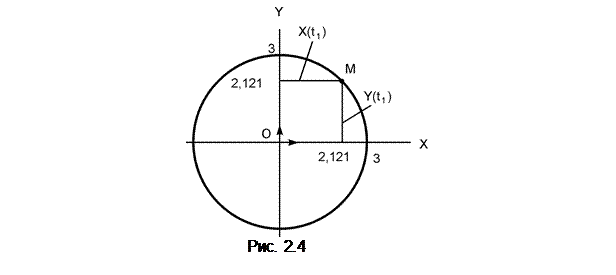
движется по окружности радиусом R = 3 см (рис. 2.4).
Определяем положение точки на траектории движения в момент времени t1.
X(t1) = 3·sin(p·t1) = 3·sin(p·0,25) = 3·0,707 = 2,121 см > 0.
Y(t1) = 3·cos(p·t1) = 3·cos(p·0,25) = 3·0,707 = 2,121 см > 0.
Показываем точку на траектории её движения (см. рис. 2.4).
ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:
1) неверно определен вид траектории движения;
2) неверно рассчитаны значения координат X(t1), Y(t1).
Прямолинейное движение точки М определяется одним уравнением движения X = f(t).
Пример. Дано: X = 10·t2 + sin(2·p·t) + 3, см (рис. 2.5).

Определить положение точки на траектории движения в начальный момент времени t0 = 0 и в момент времени t1 = 1 c.
Решение.
X(t0) = 10·(t0)2 + sin(2·p·t0) + 3 = 10·02 + sin(2·p·0) + 3 = 3 см > 0.
X(t1) = 10·(t1)2 + sin(2·p·t1) + 3 = 10·12 + sin(2·p·1) + 3 = 13 см > 0.
Значения координат X(t0), X(t1) наносим на рис. 2.5.
Скорость точки
Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта.
Скорость точки всегда направлена по касательной к траектории её движения.
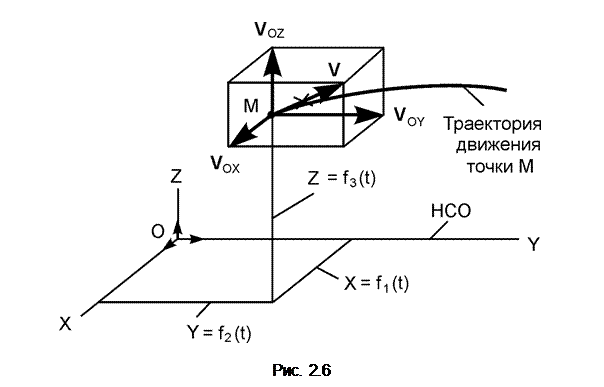 Пусть заданы уравнения движения точки в пространстве: X = f1(t); Y = f2(t); Z = f3(t) (рис. 2.6).
Пусть заданы уравнения движения точки в пространстве: X = f1(t); Y = f2(t); Z = f3(t) (рис. 2.6).
Разложим вектор V скорости точки на составляющие по координатным осям: V = V OX + V OY + V OZ. Векторы V OX, V OY, V OZ называют компонентами скорости по координатным осям. Вектор V скорости можно выразить векторным равенством:
V = i ·  + j ·
+ j · 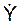 + k ·
+ k ·  ,
,
где  ,
, 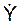 ,
,  – проекции скорости V на соответствующие координатные оси.
– проекции скорости V на соответствующие координатные оси.
В инженерных расчётах рекомендуется использовать следующие обозначения проекций скорости V на координатные оси:  ;
; 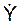 ;
;  .
.
Сравнивая последние формулы, запишем равенство
V = V OX + V OY + V OZ = i ·  + j ·
+ j · 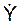 + k ·
+ k ·  .
.
Из этого равенства имеем:
V OX = i ·  ; V OY = j ·
; V OY = j · 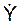 ; V OZ = k ·
; V OZ = k ·  .
.
Проекции скорости на координатные оси системы отсчёта равны первым производным по времени от соответствующих уравнений движения:
 = dX/dt;
= dX/dt;  = dY/dt;
= dY/dt;  = dZ/dt,
= dZ/dt,
где точка (·) означает символ однократного дифференцирования функции по времени.
Зная проекции скорости на координатные оси, находят модуль скорости по формуле
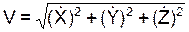 .
.
Ориентацию вектора скорости V в системе отсчёта OXYZ определяют по направляющим косинусам:
cos(V, i) =  / V; cos(V, j) =
/ V; cos(V, j) =  / V; cos(V, k) =
/ V; cos(V, k) =  / V.
/ V.
 Движение точки в плоскости OXY (рис. 2.7) задаётся двумя уравнениями движения: X = f1(t); Y = f2(t).
Движение точки в плоскости OXY (рис. 2.7) задаётся двумя уравнениями движения: X = f1(t); Y = f2(t).
Модуль и направление скорости точки в этом случае определяются по формулам:
 ;
;
 cos(V, i) =
cos(V, i) =  / V; cos(V, j) =
/ V; cos(V, j) =  / V.
/ V.
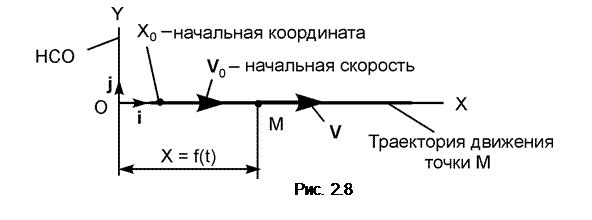 |
Прямолинейное движение точки (рис. 2.8) задаётся одним уравнением X = f(t).
В этом случае модуль скорости точки равен абсолютной величине проекции скорости на координатную ось ОХ.
V = |  | = |dX/dt|.
| = |dX/dt|.
При  > 0 точка движется в сторону увеличения координаты Х, при
> 0 точка движется в сторону увеличения координаты Х, при  < 0 – противоположно направлению оси.
< 0 – противоположно направлению оси.
Ускорение точки
Ускорение – векторная величина, характеризующая быстроту изменения величины и направления скорости.
Ускорение всегда направлено в сторону вогнутости траектории движения.
Рассматривается движение точки на плоскости в системе отсчёта OXY (рис. 2.9) по заданным уравнениям движения X = f1(t); Y = f2(t).
Согласно рис. 2.9 запишем векторное равенство
а = а ОХ +a OY = i ·  + j ·
+ j ·  ,
,
где а – ускорение точки; а ОХ, a OYкомпоненты ускорения по координатным осям;  ,
,  – проекции ускорения на координатные оси.
– проекции ускорения на координатные оси.
Здесь две точки (··) означает символ двойного дифференцирования функции по времени.

Распространяя полученный результат на пространство (система отсчёта OXYZ), получим
а = а ОХ + a OY + a OZ= i ·  + j ·
+ j ·  + j ·
+ j ·  .
.
Как правило, проекции ускорения а на координатные оси в технической литературе обозначаются так:  ,
,  ,
,  .
.
Проекции ускорения точки на координатные оси равны вторым производным по времени от соответствующих уравнений движения или первым производным по времени от проекций скорости на соответствующие оси.
 = d2X/dt2 =
= d2X/dt2 = 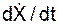 ;
;
 = d2Y/dt2 =
= d2Y/dt2 = 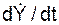 ;
;
 = d2Z/dt2 =
= d2Z/dt2 =  .
.
Модуль ускорения находится по следующим формулам:
a =  (точка движется в пространстве);
(точка движется в пространстве);
a =  (точка движется в плоскости);
(точка движется в плоскости);
a = |  |(точка движется по прямой линии).
|(точка движется по прямой линии).
Направляющие косинусы находятся по следующим формулам:
cos(a, i) =  / a; cos(a, j) =
/ a; cos(a, j) =  / a; cos(a, k) =
/ a; cos(a, k) =  / a.
/ a.
Зная направляющие косинусы, вектор ускорения а ориентируют в пространстве.
Рассматривается движение точки по прямой линии согласно заданному уравнению движения X = f(t) (рис. 2.10).
 |
При таком движении справедливо равенство а = а ОХ = i ·  . На рис. 2.10 дополнительно показано ускорение а 0–начальное ускорение точки при t0 = 0.
. На рис. 2.10 дополнительно показано ускорение а 0–начальное ускорение точки при t0 = 0.
Примечания:
1. Если проекции ускорения на координатные оси положительны ( > 0,
> 0,  > 0,
> 0,  > 0), то компоненты ускорения по координатным осям (а ОХ, a OY, a OZ) направлены в те же стороны, что и единичные векторы (I, j, k) системы отсчёта OXYZ.
> 0), то компоненты ускорения по координатным осям (а ОХ, a OY, a OZ) направлены в те же стороны, что и единичные векторы (I, j, k) системы отсчёта OXYZ.
2. Если проекции ускорения на координатные оси отрицательны ( < 0,
< 0,  < 0,
< 0,  < 0), то компоненты ускорения по координатным осям (а ОХ, a OY, a OZ ) направлены в стороны, противоположные ортам (I, j, k) системы отсчёта OXYZ.
< 0), то компоненты ускорения по координатным осям (а ОХ, a OY, a OZ ) направлены в стороны, противоположные ортам (I, j, k) системы отсчёта OXYZ.
Рассмотрим более подробно движение точки на координатной оси ОХ (рис. 2.10) по заданному уравнению движения X = f(t).
Если проекция  скорости V и проекция
скорости V и проекция  ускорения а точки совпадают по знаку, то точка движется ускоренно. При
ускорения а точки совпадают по знаку, то точка движется ускоренно. При  > 0 и
> 0 и  >0 точка движется в сторону увеличения координаты Х ускоренно. Если
>0 точка движется в сторону увеличения координаты Х ускоренно. Если  < 0 и
< 0 и  < 0, то точка движется в сторону уменьшения координаты Х ускоренно. Если
< 0, то точка движется в сторону уменьшения координаты Х ускоренно. Если  > 0 и
> 0 и  < 0, то точка движется в сторону увеличения координаты замедленно. Если
< 0, то точка движется в сторону увеличения координаты замедленно. Если  < 0 и
< 0 и  > 0, то точка движется в сторону уменьшения координаты Х замедленно.
> 0, то точка движется в сторону уменьшения координаты Х замедленно.
Если проекция  ускорения на ось ОХ постоянна (
ускорения на ось ОХ постоянна ( = const), то такое движение называют равнопеременным. При условии, что
= const), то такое движение называют равнопеременным. При условии, что  = const ≠ 0, уравнение равнопеременного движения точки записывают в виде
= const ≠ 0, уравнение равнопеременного движения точки записывают в виде
X = X0 +  0·t + (
0·t + ( ·t2)/2,
·t2)/2,
где X0 – значение координаты точки в начальный момент времени;  0 - проекция начальной скорости V 0 на координатную ось ОХ в начальный момент времени.
0 - проекция начальной скорости V 0 на координатную ось ОХ в начальный момент времени.
Если  = const > 0, то такое движение называют равноускоренным.
= const > 0, то такое движение называют равноускоренным.
Если  = const < 0, то движение точки называют равнозамедленным.
= const < 0, то движение точки называют равнозамедленным.
Если  = 0, то такое движение называют равномерным. Уравнение равномерного движения имеет вид X = X0 +
= 0, то такое движение называют равномерным. Уравнение равномерного движения имеет вид X = X0 +  ·t.
·t.
При условии, что  = f(t) ≠ const, для получения уравнения движения выражение
= f(t) ≠ const, для получения уравнения движения выражение  = f(t) необходимо дважды проинтегрировать.
= f(t) необходимо дважды проинтегрировать.
Пусть, например,  = 2·t. Представим это выражение в виде d
= 2·t. Представим это выражение в виде d  /dt = 2·t. Разделим переменные в этом дифференциальном уравнении d
/dt = 2·t. Разделим переменные в этом дифференциальном уравнении d  = 2·t·dt. Первый интеграл от этого выражения имеет вид
= 2·t·dt. Первый интеграл от этого выражения имеет вид  = 2·(t2/2) + C1 = t2 + C1, где С1 – постоянная интегрирования, которую находят по начальным условиям движения. Пусть при t0 = 0 проекция начальной скорости V 0 на ось ОХ не равна нулю:
= 2·(t2/2) + C1 = t2 + C1, где С1 – постоянная интегрирования, которую находят по начальным условиям движения. Пусть при t0 = 0 проекция начальной скорости V 0 на ось ОХ не равна нулю:  0 ≠ 0. Тогда при t0 имеем
0 ≠ 0. Тогда при t0 имеем  0 = (t0)2 + C1. Откуда С1 =
0 = (t0)2 + C1. Откуда С1 =  0. Внося значение постоянной С1 в выражение, полученное при первом интегрировании, имеем
0. Внося значение постоянной С1 в выражение, полученное при первом интегрировании, имеем  = t2 +
= t2 +  0. Так как
0. Так как  = dX/dt, то после разделения переменных имеем следующее дифференциальное уравнение движения dX = t2·dt +
= dX/dt, то после разделения переменных имеем следующее дифференциальное уравнение движения dX = t2·dt +  0·dt. Интегрируя это уравнение, получим X = t3/3 +
0·dt. Интегрируя это уравнение, получим X = t3/3 +  0·t + C2, где С2 – постоянная интегрирования, определяемая по начальным условиям движения. Пусть при t0 = 0 координата Х0 ≠ 0. Тогда X0 = (t0)3/3 +
0·t + C2, где С2 – постоянная интегрирования, определяемая по начальным условиям движения. Пусть при t0 = 0 координата Х0 ≠ 0. Тогда X0 = (t0)3/3 +  0·t0 + C2 или С2 = Х0. Окончательно имеем уравнение прямолинейного движения
0·t0 + C2 или С2 = Х0. Окончательно имеем уравнение прямолинейного движения
X = (t)3/3 +  0·t + Xo.
0·t + Xo.
Таким образом, если заданы уравнения движения точки в координатной форме, то можно в любой момент времени определить следующие кинематические характеристики:
1) траекторию движения;
2) положение точки на траектории движения;
3) проекции скорости на координатные оси, а, следовательно, и модуль скорости;
4) ориентацию вектора скорости в системе отсчёта по её направляющим косинусам;
5) проекции ускорения на координатные оси и модуль ускорения;
6) положение вектора ускорения в системе отсчёта по его направляющим косинусам.
Не нашли, что искали? Воспользуйтесь поиском: