
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пространственная произвольная
Система сил
1.26.1. Момент силы относительно оси
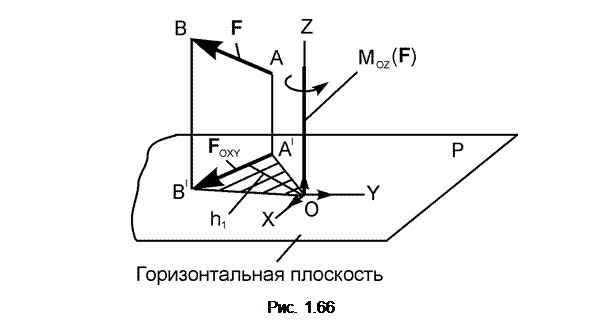 |
Положим, что к у телу в точке А приложена сила F (рис. 1.66).
Для того чтобы вычислить момент этой силы относительно оси OZ, следует спроецировать силу F на плоскость Р, перпендикулярную оси OZ, а затем вычислить момент её проекции F ОХY на эту плоскость относительно точки О пересечения оси OZ с плоскостью Р, приписав этому моменту знак «+» или «–». Отсюда следует, что момент силы относительно оси является скалярной величиной.
Моментом силы F относительно оси OZ называется взятое со знаком «+» или «–» произведение модуля проекции F OXY силы F на плоскость, перпендикулярную оси, на её плечо h1 относительно точки О пересечения оси с плоскостью P.
MОZ(F) = ± FОХY·h1.
Момент силы относительно оси считается положительным, если, смотря навстречу оси OZ, можно видеть проекцию F ОХY силы F, стремящейся вращать плоскость Р относительно оси OZ в сторону, противоположную вращению часовой стрелки.
Момент силы относительно оси изображается отрезком, отложенным на оси OZ от точки О в положительном направлении, если MOZ(F) > 0, и в отрицательном – если MOZ(F) < 0.
Момент силы относительно оси равен нулю в двух случаях:
1) если F ОХY = 0, т. е. линия действия силы параллельна оси;
2) если h1 = 0, т. е. линия действия силы пересекает ось.
Таким образом, если сила и ось лежат в одной плоскости, то момент силы относительно оси равен нулю.
1.26.2. Аналитические выражения моментов
силы относительно координатных осей
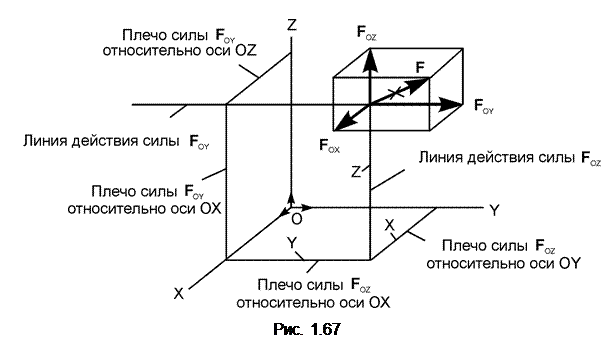
Разложим силу F на компоненты по координатным осям OX, OY, OZ (рис. 1.67):
F = F ОХ + F OY + F OZ.
Смотря с положительного направления отсчёта каждой из координатных осей, определим, какие из компонент F OX, F OY, F OZ вызывают вращение параллелепипеда относительно этих осей. При этом плечами сил FOX, FOY, FOZ относительно соответствующих координатных осей называются кратчайшие расстояния от линий их действия до соответствующих осей. Так, плечо силы F OY относительно оси ОХ равно модулю координаты Z, а плечо силы F OZ относительно оси ОХ равно модулю координаты Y.
Как и ранее, момент силы относительно оси считается положительным, если, смотря с положительных направлений координатных осей, можно видеть силы F OX, F OY, F OZ, поворачивающие параллелепипед в стороны, противоположные вращению часовой стрелки.
MOX(F) = FOZ·IYI – FOY·IZI;
MOY(F) = FOX·IZI – FOZ·IXI;
MOZ(F) = FOY·IXI – FOX·IYI.
В полученных выражениях IXI, IYI, IZI – модули координат точки приложения силы F.
Таким образом, для того чтобы определить момент силы относительно оси, силу F раскладывают на компоненты по координатным осям и затем находят моменты составляющих этих компонент относительно соответствующих координатных осей.
Необходимо еще раз отметить, что силы, параллельные координатным осям, вращения параллелепипеда относительно этих осей не производят.
1.26.3. Приведение пространственной произвольной
системы сил к заданному центру
Пространственная произвольная система сил – система сил, линии действия которых как угодно произвольно расположены в пространстве.
В качестве примера рассмотрим (рис. 1.68) пространственную систему сил (F 1, F 2, F 3). При этом сила F 1 лежит в плоскости OXY и параллельна оси ОY. Сила F 2 лежит в плоскости OYZ и параллельна оси OZ. Сила F 3 лежит в плоскости OXZ и параллельна оси OX.
Последовательно применяя метод Пуансо к заданной системе сил, приведём её к началу систему отсчёта OXYZ. Тогда система сил (F 1, F 2, F 3) будет эквивалентна системе сил (F 1, F 2, F 3) и системе присоединённых пар сил (M O(F 1), M O(F 2), M O(F 3)), приложенных в точке О. Так как система векторов приложена в одной точке, то одноимённые векторы можно сложить. В результате этих операций получим главный вектор сил R * = F 1 + F 2 + F 3 и главный момент присоединённых пар сил M * = M O(F 1) + M O(F 2) + M O(F 3).
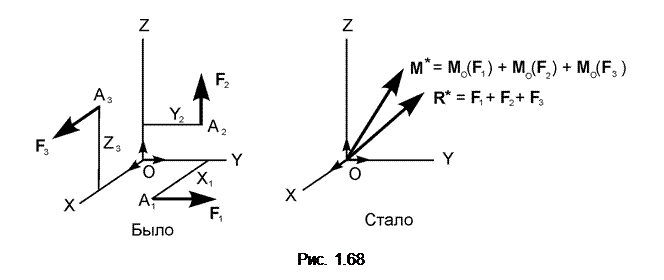
Таким образом, система сил (F 1, F 2, F 3) заменена одной силой R * и одной парой сил с моментом M *. Согласно методу Пуансо главный вектор сил R * не зависит от положения точки приведения и может быть помещён в любую точку пространства.
Полученный вывод можно распространить на любую произвольную пространственную систему сил.
Модуль и направление главного вектора R * определяют по формулам:
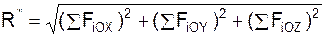 ;
;
cos(R *, i) = ∑ FiOX/R*;
cos(R *, j) = ∑ FiOY/R*;
cos(R *, k) = ∑ FiOZ/R*.
Модуль и направление главного момента М * определяют по следующим формулам:
 ;
;
cos(М *, i) = ∑МiOX/М*;
cos(М *, j) = ∑МiOY/М*;
cos(М *, k) = ∑МiOZ/М*.
Момент каждой из сил относительно координатных осей вычисляют по формулам:
MiOX = FiOZ·IYiI – FiOY·IZiI;
MiOY = FiOX·IZiI – FiOZ·IXiI;
MiOZ = FiOY·IXiI – FiOX·IYiI.
1.26.4. Уравнения равновесия
пространственной системы сил
Напомним, что к внешним силам относятся активные силы F iE и реакции R iE внешних связей.
Аналитические условия равновесия пространственной произвольной системы сил выражаются совокупностью следующих уравнений:
Σ 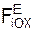 + Σ
+ Σ 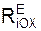 = 0;
= 0;
Σ 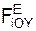 + Σ
+ Σ 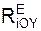 = 0;
= 0;
Σ 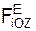 + Σ
+ Σ 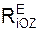 = 0;
= 0;
Σ MOX(F iE) + Σ MOX(R iE) = 0;
Σ MOY(F iE) + Σ MOY(R iE) = 0;
Σ MOZ(F iE) + Σ MOZ(R iE) = 0.
Таким образом, для равновесия пространственной произвольной системы сил необходимо и достаточно, чтобы суммы проекций активных сил и реакций внешних связей на координатные оси системы отсчёта, а также и суммы моментов этих сил относительно соответствующих осей равнялись нулю.
Для пространственной системы сил, линии действия которых параллельны оси OZ, аналитические условия равновесия имеют вид:
Σ 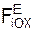 + Σ
+ Σ 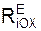 = 0;
= 0;
Σ MOX(F iE) + Σ MOX(R iE) = 0;
Σ MOY(F iE) + Σ MOY(R iE) = 0.
Для пространственной сходящейся системы сил имеем три уравнения равновесия:
Σ 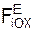 + Σ
+ Σ 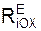 = 0;
= 0;
Σ 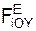 + Σ
+ Σ 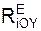 = 0;
= 0;
Σ 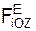 + Σ
+ Σ 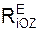 = 0.
= 0.
1.26.5. Типы связей в пространстве
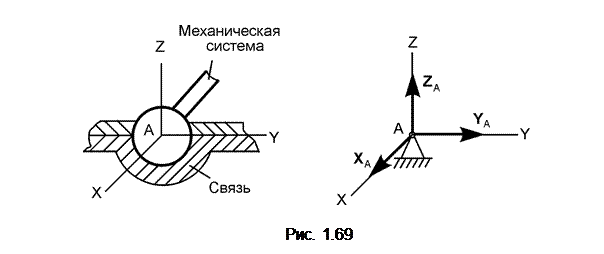 |
На рис. 1.69 изображен шаровый шарнир. Он представляет собой шар, который может вращаться как угодно внутри сферической поверхности. Центр шара остается неподвижной точкой, через которую проходит линия действия реакции R A.
Направление реакции R A заранее неизвестно, поэтому её раскладывают на компоненты X A, Y A, Z A по координатным осям OX, OY, OZ:
R A = X A + Y A + Z A.
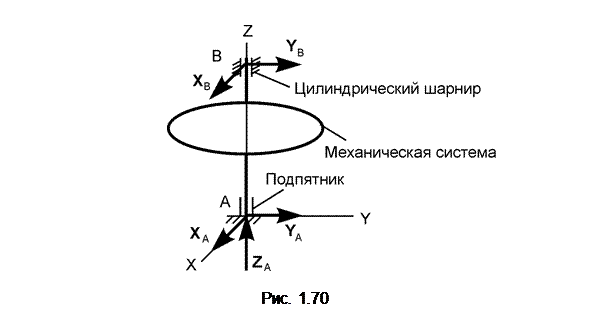 |
На рис. 1.70 изображена механическая система, на которую наложены связи: подпятник в точке А и цилиндрический шарнир в точке В.
Направления реакций в точках А и В заранее неизвестны, поэтому их раскладывают на компоненты по координатным осям.
R A = X A + Y A + Z A; R B = X B + Y B.
На рис. 1.71 изображена механическая система, на которую наложена связь – жёсткая заделка в пространстве.
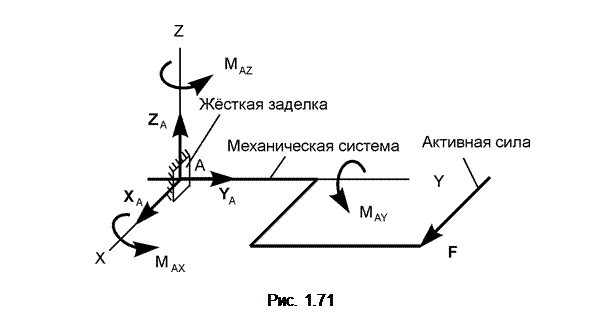
Эта связь не позволяет перемещаться телу в пространстве в любом направлении вдоль координатных осей системы отсчёта и совершать вращательные движения относительно этих осей. Реакция такой связи состоит из трёх сил X A, Y A, Z A и трёх реактивных моментов MAX, MAY, MAZ.
Варианты курсового задания С 4
«Определение реакций опор твёрдого тела»
Для закрепления изложенного теоретического материала необходимо выполнить курсовое задание С 4.
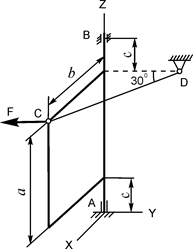
В вариантах 1 - 15 этого курсового задания (табл. 1.4) рассматривается равновесие однородной прямоугольной плиты с размерами a и b и весом G. На плиту действует активная сила F, которая параллельна соответствующей координатной оси системы отсчёта OXYZ. Требуется определить реакции внешних связей, наложенных на плиту. По условию задания CD – невесомый стержень.
В вариантах 16 – 30 рассматривается равновесие вала, на котором установлены два круглых колеса с радиусами R1, R2. Эти колёса загружены активными силами F 1 – F 5. По условию задания активные силы параллельны соответствующим координатным осям системы отсчёта OXYZ. Требуется определить реакции внешних связей, наложенных на конструкцию, и величину силы F 4.
Исходные данные для расчёта и определяемые величины приведены в табл. 1.4.
Таблица 1.4
| Номер варианта | Расчётная схема | Исходные данные | Определяемые величины |

| G = 8 кН; F = 5 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? ZB =? RC =? | |

| G = 8 кН; F = 6 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? XB =? RC =? |
Продолжение табл. 1.4
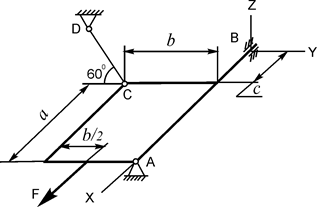
| G = 8 кН; F = 7 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? ZB =? RC =? | |

| G = 8 кН; F = 8 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? ZB =? RC =? | |
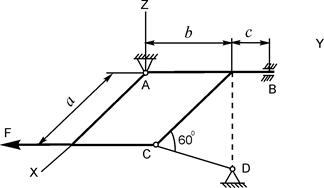
| G = 8 кН; F = 9 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? XB =? ZB =? RC =? |
Продолжение табл. 1.4

| G = 8 кН; F = 10 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? XB =? RC =? | |
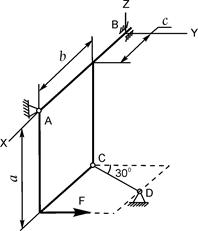
| G = 8 кН; F = 4 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? ZB =? RC =? | |
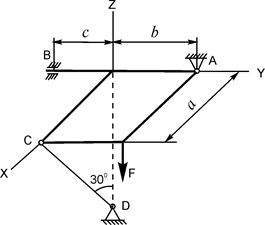
| G = 8 кН; F = 3 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? XB =? ZB =? RC =? |
Продолжение табл. 1.4
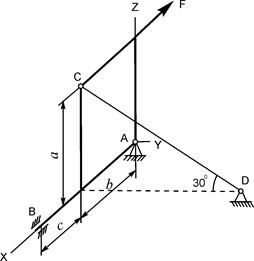
| G = 8 кН; F = 2 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? YB =? ZB =? RC =? | |

| G = 8 кН; F = 2 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? XB =? ZB =? RC =? | |
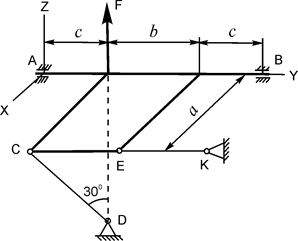
| G = 8 кН; F = 5 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? ZA =? ХВ =? ZB =? RC =? RE =? |
Продолжение табл. 1.4
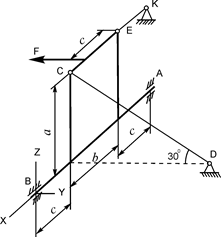
| G = 8 кН; F = 6 кН; a = 3 м; b = 2 м; c = 0,2 м | YA =? ZA =? YB =? ZB =? RC =? RE =? | ||

| G = 8 кН; F = 4 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? ZA =? XB =? ZB =? RC =? | ||

| G = 8 кН; F = 10 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? XB =? YB =? RC =? | ||
Продолжение табл. 1.4
| G = 8 кН; F = 8 кН; a = 3 м; b = 2 м; c = 0,2 м | XA =? YA =? ZA =? XB =? YB =? RC =? | |
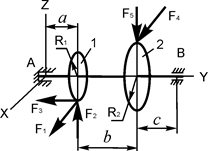
| F1 = 4 кН; F2 =1,2 кН; F3 =0,4 кН; F5 =0,5 кН; R1=0,09 м; R2=0,27 м; a = 0,1 м; b = 0,2 м; с = 0,1м | XA =? YA =? ZA =? XB =? ZB =? F4 =? | |
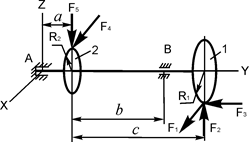
| F1 = 10 кН; F2 = 3 кН; F3 = 1 кН; F5 = 1,5 кН; R1 = 0,05 м; R2 = 0,12 м; a = 0,1 м; b = 0,15 м; с = 0,22м | XA =? YA =? ZA =? XB =? ZB =? F4 =? | |
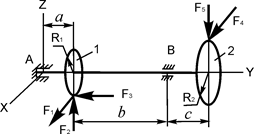
| F1 = 8 кН; F2 = 2,5 кН; F3 = 1 кН; F5 = 2 кН; R1 = 0,2 м; R2 = 0,3 м; a = 0,1 м; b = 0,12 м; с = 0,2м | XA =? YA =? ZA =? XB =? ZB =? F4 =? |
Продолжение табл. 1.4

| F1 = 12 кН; F2 = 4 кН; F3 = 1,5 кН; F5 = 2 кН; R1 = 0,1 м; R2 = 0,2 м; a = 0,1 м; b = 0,2 м; с = 0,4м | XA =? YA =? ZA =? XB =? ZB =? F4 =? | |
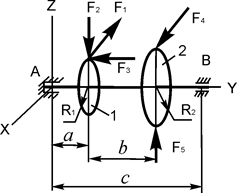
| F1 = 3 кН; F2 = 1 кН; F3 = 0,5 кН; F5 = 1,2 кН; R1 = 0,07 м; R2 = 0,25 м; a = 0,12 м; b = 0,15 м; с = 0,45м | XA =? YA =? ZA =? XB =? ZB =? F4 =? | |
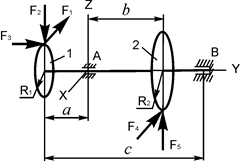
| F1 = 9 кН; F2 = 3,5 кН; F3 = 2 кН; F5 = 1,25 кН; R1 = 0,06 м; R2 = 0,15 м; a = 0,2 м; b = 0,3 м; с = 0,7м | XA =? ZA =? XB =? YB =? ZB =? F4 =? | |

| F1 = 3 кН; F2 = 1 кН; F3 = 0,5 кН; F5 = 2,5 кН; R1 = 0,15 м; R2 = 0,18 м; a = 0,1 м; b = 0,12 м; с = 0,3м | XA =? ZA =? XB =? YB =? ZB =? F4 =? |
Продолжение табл. 1.4

| F1 = 7 кН; F2 = 2,8 кН; F3 = 0,8 кН; F5 = 4 кН; R1 = 0,07 м; R2 = 0,12 м; a = 0,12 м; b = 0,2 м; с = 0,47м | XA =? ZA =? XB =? YB =? ZB =? F4 =? | |
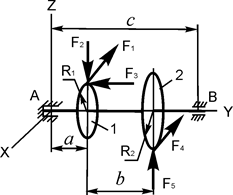
| F1 = 6 кН; F2 = 2 кН; F3 = 0,6 кН; F5 = 2,5 кН; R1 = 0,06 м; R2 = 0,16 м; a = 0,2 м; b = 0,25 м; с = 0,55м | XA =? YA =? ZA =? XB =? ZB =? F4 =? | |
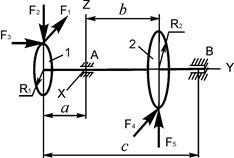
| F1 = 11 кН; F2 = 4 кН; F3 = 2 кН; F5 = 5 кН; R1 = 0,1 м; R2 = 0,2 м; a = 0,1 м; b = 0,12 м; с = 0,3м | XA =? ZA =? XB =? YB =? ZB =? F4 =? | |
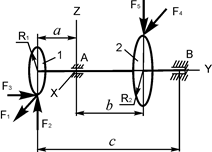
| F1 = 2 кН; F2 = 0,8 кН; F3 = 0,2 кН; F5 = 1 кН; R1 = 0,05 м; R2 = 0,12 м; a = 0,14 м; b = 0,11 м; с = 0,45м | XA =? ZA =? XB =? YB =? ZB =? F4 =? |
Окончание табл.1.4
Не нашли, что искали? Воспользуйтесь поиском: