
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример выполнения курсового задания К 1
Исходные данные: X = X(t) = 2·cos(p·t2/3) – 2; см. (1)
Y = Y(t) = – 2·sin(p·t2/3) + 3; см. (2)
t1 = 1 c.
По заданным уравнениям движения точки на плоскости определить кинематические характеристики в момент времени t1.
Решение.
1. Для определения траектории движения точки уравнения (1) и (2) связываются через параметр t. Уравнения (1) и (2) выразим в следующем виде:
X + 2 = 2·cos(p·t2/3); (1I)
Y – 3 = – 2·sin(p·t2/3). (2I)
Возведём в квадрат левые и правые части уравнений (1I), (2I) и сложим их.
(X + 2)2 = (2·cos(p·t2/3))2; (1II)
+
(Y – 3)2 = (– 2·sin(p·t2/3))2. (2II)
После сложения уравнений (1II), (2II) получим
(X + 2)2 + (Y – 3)2 = (2·cos(p·t2/3))2 + (– 2·sin(p·t2/3))2 =
= 22·((cos(p·t2/3))2 + (sin(p·t2/3)))2 = 22·1 = 22.
При преобразованиях использована тригонометрическая формула sin2(α) + cos2(α) = 1. Полученное уравнение
(X + 2)2 + (Y– 3)2 = 22
есть уравнение окружности (x – a)2+(y – b)2 = r2 c центром в точке с координатами (a, b). Построим график траектории движения точки (рис. 2.17).
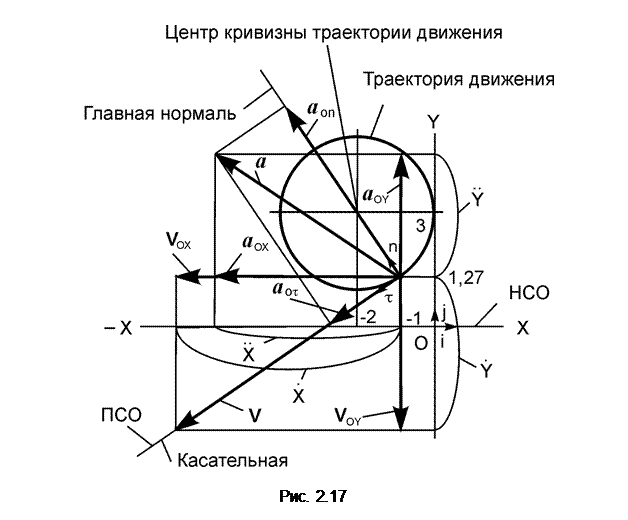
2. Определение положения точки на траектории её движения в момент времени (t1).
В уравнения (1) и (2) подставляем время t1.
X(t1) = 2·cos(p·(t1)2/3) – 2 = 2·cos(p·(1)2/3) – 2 =
= 2·0,5 – 2 = 1,000 см < 0.
Y(t1) = – 2·sin(p·(t1)2/3) + 3 = – 2·sin(p·(1)2/3) + 3 =
= – 2·0,866 + 3 = 1,270 см > 0.
Точку с координатами (–1, 1,270) показываем на траектории её движения.
ВНИМАНИЕ!
Если точка не попала на траекторию её движения, то:
1) неверно определена траектория движения;
2) неверно подсчитаны значения координат точки.
3. Определение скорости точки.
Для определения скорости точки найдем производные по времени от соответствующих уравнений её движения:
 = 2·(– sin(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(sin(p·t2/3))·t;
= 2·(– sin(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(sin(p·t2/3))·t;
 = – 2·(cos(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(cos(p·t2/3))·t.
= – 2·(cos(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(cos(p·t2/3))·t.
Вычислим значения проекций  ,
,  скорости на оси OX и OY в момент времени t1:
скорости на оси OX и OY в момент времени t1:
 (t1) = (– 4·p/3)·(sin(p·(t1)2/3))·t1 =
(t1) = (– 4·p/3)·(sin(p·(t1)2/3))·t1 =
=(– 4·3,14/3)·sin(p·12/3)·1 = – 3,625 см/с < 0;
 (t1) = (– 4·p/3)·(cos(p·(t1)2/3))·t1 =
(t1) = (– 4·p/3)·(cos(p·(t1)2/3))·t1 =
=(– 4·3,14/3)·cos(p·12/3)·1 = – 2,093 см/с < 0.
Так как  (t1) и
(t1) и  (t1) меньше нуля, то векторы V OX, V OY направлены в стороны, противоположные векторам i, j. В выбранном масштабе наносим векторы V OX, V OY на чертёж (рис. 2.17).
(t1) меньше нуля, то векторы V OX, V OY направлены в стороны, противоположные векторам i, j. В выбранном масштабе наносим векторы V OX, V OY на чертёж (рис. 2.17).
На векторах V OX, V OY строим вектор V по правилу параллелограмма. Вектор скорости V направлен по касательной к траектории движения точки.
ВНИМАНИЕ!
Если вектор V направлен не по касательной к траектории движения, то:
1) неверно взяты производные  ,
,  ;
;
2) неверно вычислены значения  (t1),
(t1),  (t1).
(t1).
Вычисляется модуль V скорости V в момент времени (t1) по формуле
 =
=
=  = 4,186 см/с.
= 4,186 см/с.
В ряде вариантов можно определить модуль скорости по формуле
 = =
= =  =
=
= 4·p·t/3.
V(t1) = 4·p·t1/3 = 4·3,14·1/3 = 4,186 см/с.
4. Определение ускорения точки.
Находятся производные по времени от проекций  ,
,  скорости на координатные оси OX, OY.
скорости на координатные оси OX, OY.
Так как проекция  скорости на ось ОХ представляет собой произведение двух переменных ((– 4·p/3)·sin(p·t2/3) и t), то по правилу дифференцирования произведения получим
скорости на ось ОХ представляет собой произведение двух переменных ((– 4·p/3)·sin(p·t2/3) и t), то по правилу дифференцирования произведения получим
 (– 8·p2/9)·cos(p·t2/3)·t2 – (4·p/3)·sin(p·t2/3).
(– 8·p2/9)·cos(p·t2/3)·t2 – (4·p/3)·sin(p·t2/3).
Аналогично
 (8·p2/9)·sin(p·t2/3)·t2 – (4·p/3)·cos(p·t2/3).
(8·p2/9)·sin(p·t2/3)·t2 – (4·p/3)·cos(p·t2/3).
Определим 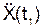 и
и  , подставляя в последние формулы значение времени t1. Произведя расчеты, получим:
, подставляя в последние формулы значение времени t1. Произведя расчеты, получим:
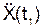 = – 8,020 см/с2;
= – 8,020 см/с2;  = 5,510 см/с2.
= 5,510 см/с2.
Так как 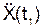 <0, то вектор a OX направлен в сторону, противоположную орту i. Вектор a OY направлен в ту же сторону, что и вектор j, так как
<0, то вектор a OX направлен в сторону, противоположную орту i. Вектор a OY направлен в ту же сторону, что и вектор j, так как  >0. На векторах a OX и a OY строим вектор ускорения a. Вектор ускорения a всегда направлен в сторону вогнутости траектории.
>0. На векторах a OX и a OY строим вектор ускорения a. Вектор ускорения a всегда направлен в сторону вогнутости траектории.
ВНИМАНИЕ!
Если ускорение a направлено не в сторону вогнутости траектории движения, то:
1) неверно взяты производные  ,
,  ;
;
2) неверно вычислены значения 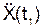 ,
,  .
.
Определяется модуль ускорения по формуле
a (t1) =  =
=  = 9,730 см/с2.
= 9,730 см/с2.
5. Определение касательного и нормального ускорений.
На рис. 2.17 наносим подвижную систему отсчёта (ПСО). Разложим полное ускорение a на касательное а oτ и нормальное а on ускорения. Так как касательное ускорение а oτ совпадает с направлением скорости V, то точка движется ускоренно. Модуль а oτ касательного ускорения в момент времени t1 находится по формуле
а oτ(t1) = | 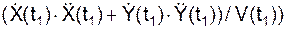 | = |
| = |  (t1)| =
(t1)| =
= |((– 3,625)·(– 8,020) + (– 2,099)·5,510)/4,186| = 4,186 см/с2.
Касательное ускорение характеризует быстроту изменения величины скорости, поэтому его проекция на касательную может быть определена по формуле
 = dV/dt = d(4pt/3)/dt = 4p/3 = 4·3,14/3 = 4,186 см/с2 = const > 0.
= dV/dt = d(4pt/3)/dt = 4p/3 = 4·3,14/3 = 4,186 см/с2 = const > 0.
Так как  = const и направления а oτ и V совпадают, то точка движется по окружности равноускоренно. а oτ =
= const и направления а oτ и V совпадают, то точка движется по окружности равноускоренно. а oτ =  = const.
= const.
Модуль нормального ускорения находится по формуле
а on(t1) = 
 =
=
=  = 8,780 см/с2.
= 8,780 см/с2.
Из формулы а on = V2/ρ определяется радиус кривизны траектории движения ρ(t1) = V2(t1)/(а on(t1)) = (4,186)2/8,780 = 2,0 см. Таким образом, радиус кривизны траектории движения равен радиусу окружности, по которому перемещается точка.
Результаты вычислений заносятся в таблицу.
Таблица
| X(t1), см | Y(t1), см |  , см/с , см/с
|  , см/с , см/с
|  , см/с2 , см/с2
|  , см/с2 , см/с2
|
| – 1,00 | 1,27 | – 3,63 | – 2,09 | – 8,02 | 5,51 |
Окончание таблицы
| V(t1), см/с | а (t1), см/с2 | а oτ(t1), см/с2 | а on(t1), см/с2 | ρ(t1), см | |
| 4,19 | 9,73 | 4,20 | 8,78 | 2,00 |
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «кинематика».
2. Сформулировать определение термина «механическое движение».
3. Записать уравнения движения точки в декартовой системе отсчёта (точка движется в пространстве).
4. Записать уравнения движения точки в декартовой системе отсчёта (точка движется в горизонтальной плоскости).
5. Записать уравнения движения точки в декартовой системе отсчёта (точка движется параллельно оси ОХ).
6. Записать уравнение траектории движения точки в декартовой системе отсчёта (точка движется в вертикальной плоскости OYZ).
7. Сформулировать определение термина «скорость».
8. Записать формулу для определения скорости точки через компоненты скорости в декартовой системе отсчёта.
9.Записать формулы для определения проекций скорости на координатные оси в декартовой системе отсчёта.
10. Записать формулу для определения модуля скорости через её проекции в декартовой системе отсчёта.
11. Записать формулы для определения направляющих косинусов при ориентации скорости в декартовой системе отсчёта.
12. Как направлена скорость точки по отношению к траектории её движения?
13. Сформулировать определение термина «ускорение».
14. Куда направлено ускорение точки по отношению к криволинейной траектории её движения?
15. Записать формулу для определения ускорения точки через компоненты ускорения в декартовой системе отсчёта.
16. Записать формулы для определения проекций ускорения на координатные оси в декартовой системе отсчёта.
17. Записать формулу для определения модуля ускорения через его проекции в декартовой системе отсчёта.
18. Записать формулы для определения направляющих косинусов при ориентации ускорения в декартовой системе отсчёта.
19. Записать уравнение равнопеременного прямолинейного движения точки в декартовой системе отсчёта.
20. Записать формулу равномерного прямолинейного движения точки в декартовой системе отсчёта.
21. Записать уравнение движения точки в естественных координатах.
22. Записать формулу для определения вектора скорости точки в естественных координатах.
23. При каком условии точка движется в сторону увеличения дуговой координаты?
24. При каком условии точка движется в сторону уменьшения дуговой координаты?
25. Записать формулу для определения модуля скорости в естественных координатах.
26. Записать формулу для определения вектора ускорения в естественных координатах.
27. Сформулировать определение термина «касательное ускорение».
28. Сформулировать определение термина «нормальное ускорение».
29. Записать формулу для определения вектора касательного ускорения.
30. Записать формулу для определения вектора нормального ускорения.
31. Записать формулу для определения модуля ускорения точки при естественном способе задания движения точки.
32. Записать формулу для определения модуля касательного ускорения с использованием проекций скорости и ускорения на координатные оси декартовой системы отсчёта.
33. Как движется точка, если проекции её скорости и ускорения на касательную совпадают по знакам?
34. Как движется точка, если проекции её скорости и ускорения на касательную не совпадают по знакам?
35. Что характеризует касательное ускорение?
36. Что характеризует нормальное ускорение?
37. Чему равен радиус кривизны траектории при прямолинейном движении точки?
38. При каких условиях происходит прямолинейное движение точки?
39. При каких условиях происходит равномерное криволинейное движение?
40. При каких условиях происходит неравномерное криволинейное движение?
41. Записать уравнение движения точки при векторном способе задания её движения.
42. Записать формулу для определения скорости точки при векторном способе задания её движения.
43. Записать формулу для определения ускорения точки при задании её движения векторным способом.
44. Записать уравнение равнопеременного движения точки в естественных координатах.
45. Записать уравнение равномерного движения точки в естественных координатах.
2.14. Поступательное движение твёрдого тела
 Поступательным движением твёрдого тела называется такое движение, при котором любая прямая линия, проведенная на теле, остается во всё время движения тела параллельной своему начальному положению (рис. 2.18).
Поступательным движением твёрдого тела называется такое движение, при котором любая прямая линия, проведенная на теле, остается во всё время движения тела параллельной своему начальному положению (рис. 2.18).
При поступательном движении траектории всех точек тела одинаковы (при наложении друг на друга траектории движения точек А, В, С совпадают), а скорости и ускорения всех точек геометрически равны:
V A = V B = V C = …; a A= a B= a С=….
Эти свойства позволяют свести изучение поступательного движения тела к изучению движения его отдельной точки, т. е. к задаче кинематики точки. За такую точку, как правило, выбирают центр тяжести (центр масс) тела.
Рассматривается поступательное движение тела, при котором все его точки перемещаются параллельно неподвижной плоскости OXY (рис. 2.19).
Выражения XC = f1(t), YC = f2(t), описывающие движение центра С тяжести тела называют уравнениями поступательного движения твёрдого тела на плоскости.
Уравнений поступательного движения в пространстве три, а при прямолинейном поступательном движении – одно.

Таким образом, для тела при его поступательном движении имеем следующие выражения:
– уравнения поступательного движения тела в пространстве:
XC = f1(t), YC = f2(t), ZC = f3(t);
– уравнения поступательного движения тела параллельно плоскости OXY:
XC = f1(t), YC = f2(t);
– уравнение поступательного движения тела параллельно координатной оси ОХ
XC = f1(t).
Если заданы уравнения поступательного движения тела, то несложно определить скорость V C и ускорение a Сцентра масс, а следовательно, и скорость, и ускорение любой точки этого тела по следующим формулам.
Проекции  ,
,  ,
,  скорости V C центра масс на координатные оси:
скорости V C центра масс на координатные оси:
 = dXC/dt;
= dXC/dt;  = dYC/dt;
= dYC/dt;  = dZC/dt.
= dZC/dt.
Модуль VC скорости центра масс
VC =  .
.
Направляющие косинусы:
cos(V C, i) =  / VC; cos(V C, j) =
/ VC; cos(V C, j) =  / VC;
/ VC;
cos(V C, k) =  / VC.
/ VC.
Проекции  ,
,  ,
,  ускорения центра масс на координатные оси:
ускорения центра масс на координатные оси:
 =
=  = d2XC/dt2;
= d2XC/dt2;
 = d2YC/dt2;
= d2YC/dt2;
 = d2ZC/dt2.
= d2ZC/dt2.
Модуль ускорения центра масс
a С =  .
.
Направляющие косинусы:
cos(a С , i) =  / a С; cos(a С , j) =
/ a С; cos(a С , j) =  / a С; cos(a С , k) =
/ a С; cos(a С , k) =  / a С.
/ a С.
Таким образом, зная уравнения поступательного движения тела, можно найти следующие кинематические характеристики:
1) траекторию движения;
2) положение тела на траектории движения в любой момент времени;
3) скорость любой точки и ориентацию вектора этой скорости в пространстве;
4) ускорение любой точки и ориентацию вектора этого ускорения в пространстве в любой момент времени.
Поступательное движение является простейшим видом движения твёрдого тела.
2.15. Вращательное движение твёрдого тела
Вращательным движением твёрдого тела называется такое его движение, при котором все точки, находящиеся на прямой, неизменно связанной с телом и называемой осью вращения, остаются неподвижными.
Таким образом, при вращательном движении твёрдого тела ось вращения всегда неподвижна (рис. 2.20).
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на неподвижной оси вращения.
При вращении тела угол его поворота φ изменяется в зависимости от времени t:

φ = f(t).
Эту аналитическую зависимость (φ = f(t)) называют уравнением вращательного движения твёрдого тела. Она полностью определяет положение тела в пространстве в любой момент времени.
На рис. 2.20 показано направление положительного отсчёта угла поворота φ. Угол φ измеряется в рад.
Пусть, например, задано уравнение вращательного движения
φ = p·t2 + 2·p·t + p/4 (рад).
Величина, характеризующая быстроту изменения угла поворота φ с течением времени, называется угловой скоростью и обозначается  .
.
Угловая скорость  равна производной по времени от уравнения φ = f(t) вращательного движения твердого тела:
равна производной по времени от уравнения φ = f(t) вращательного движения твердого тела:
 = dφ/dt.
= dφ/dt.
Угловую скорость принято обозначать  , где (·) – символ дифференцирования функции φ = f(t) по времени.
, где (·) – символ дифференцирования функции φ = f(t) по времени.
Для приведенного примера уравнения вращательного движения тела φ = pt2 + 2pt + p/4 имеем  = dφ/dt = 2pt + 2p.
= dφ/dt = 2pt + 2p.
Угловая скорость измеряется в рад/с.
Если  > 0, то угол поворота φ увеличивается, т. е. вращение тела происходит в положительном направлении отсчёта угла поворота.
> 0, то угол поворота φ увеличивается, т. е. вращение тела происходит в положительном направлении отсчёта угла поворота.
Если  < 0, то угол поворота φ уменьшается, т. е. тело вращается в сторону отрицательного направления отсчёта угла φ.
< 0, то угол поворота φ уменьшается, т. е. тело вращается в сторону отрицательного направления отсчёта угла φ.
Если  при переходе значения
при переходе значения  = 0, непрерывно изменяясь, меняет знак, то угол поворота φ в этот момент времени достигает максимума или минимума, т. е. изменяется направление вращения тела.
= 0, непрерывно изменяясь, меняет знак, то угол поворота φ в этот момент времени достигает максимума или минимума, т. е. изменяется направление вращения тела.
Таким образом, знак производной  указывает направление вращения тела.
указывает направление вращения тела.
Модуль угловой скорости обозначают символом ω. Отсюда имеем ω = I  I.
I.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Угловое ускорение принято обозначать  , где (··) – символ двойного дифференцирования функции φ = f(t) по времени.
, где (··) – символ двойного дифференцирования функции φ = f(t) по времени.
Угловое ускорение  равно второй производной по времени от угла поворота φ или первой производной по времени от угловой скорости
равно второй производной по времени от угла поворота φ или первой производной по времени от угловой скорости  :
:
 = d2φ/dt2 = d
= d2φ/dt2 = d  /dt.
/dt.
Для рассматриваемого случая имеем
 = d
= d  /dt = d(2·p·t + 2·p)/dt = 2·p рад/с2 = const > 0.
/dt = d(2·p·t + 2·p)/dt = 2·p рад/с2 = const > 0.
Угловое ускорение  имеет размерность рад/с2. Модуль углового ускорения обозначают символом ε. Исходя из этого, имеем ε = I
имеет размерность рад/с2. Модуль углового ускорения обозначают символом ε. Исходя из этого, имеем ε = I  I.
I.
Если знаки  и
и  совпадают, то вращение тела происходит ускоренно:
совпадают, то вращение тела происходит ускоренно:
1)  > 0 и
> 0 и  > 0 – происходит ускоренное вращение тела, величина угла φ возрастает;
> 0 – происходит ускоренное вращение тела, величина угла φ возрастает;
2)  < 0 и
< 0 и  < 0 – величина угла поворота φ ускоренно уменьшается.
< 0 – величина угла поворота φ ускоренно уменьшается.
Если знаки  и
и  не совпадают, то происходит замедленное вращение тела:
не совпадают, то происходит замедленное вращение тела:
1)  > 0 и
> 0 и  < 0 – угол поворота φ возрастает замедленно;
< 0 – угол поворота φ возрастает замедленно;
2)  < 0 и
< 0 и  > 0 – величина угла поворота φ замедленно уменьшается.
> 0 – величина угла поворота φ замедленно уменьшается.
Если угловое ускорение  = 0 = const, то происходит равномерное вращение тела, при котором угловая скорость
= 0 = const, то происходит равномерное вращение тела, при котором угловая скорость  постоянна. Уравнение равномерного вращения имеет вид
постоянна. Уравнение равномерного вращения имеет вид
φ = f(t) = φ0 +  ·t.
·t.
Если начальный угол поворота φ0 = 0, то φ = f(t) =  ·t. Из уравнения равномерного вращения имеем
·t. Из уравнения равномерного вращения имеем  = (φ – φ0)/t, т. е. угловая скорость равномерного вращения тела равна отношению угла поворота за некоторый промежуток времени к этому промежутку времени.
= (φ – φ0)/t, т. е. угловая скорость равномерного вращения тела равна отношению угла поворота за некоторый промежуток времени к этому промежутку времени.
Число оборотов, совершаемых вращающимся телом за единицу времени (обычно за минуту), называется частотой вращения и обозначается n (об/мин). Так как один оборот равен 2·p радиан, то зависимость между модулем ω угловой скорости  (рад/с) и частотой вращения имеет вид
(рад/с) и частотой вращения имеет вид
ω = 2·p·n/60 = p·n/30.
Вращение тела, при котором угловое ускорение постоянно и не равно нулю ( = C1 = const ≠ 0), называют равнопеременным вращением. При этом если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается – равнозамедленным. Уравнение равнопеременного вращения имеет вид
= C1 = const ≠ 0), называют равнопеременным вращением. При этом если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается – равнозамедленным. Уравнение равнопеременного вращения имеет вид
φ = φ(t) = φ0 +  ·t + (
·t + ( ·t2)/2.
·t2)/2.
При дифференцировании этого уравнения получим угловую скорость
 = dφ/dt =
= dφ/dt =  +
+  ·t.
·t.
Угловая скорость  и угловое ускорение
и угловое ускорение  являются векторными величинами и обозначаются символами
являются векторными величинами и обозначаются символами  ,
,  . Условимся откладывать вектор угловой скорости
. Условимся откладывать вектор угловой скорости  от любой точки оси вращения, направляя его по этой оси так, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим в сторону, противоположную вращению часовой стрелки (рис. 2.21).
от любой точки оси вращения, направляя его по этой оси так, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим в сторону, противоположную вращению часовой стрелки (рис. 2.21).

Принятое правило обусловлено применением правой системы отсчёта, которой соответствует положительное направление вращения в сторону, противоположную вращению часовой стрелки.
Вектор углового ускорения  характеризует изменение вектора угловой скорости
характеризует изменение вектора угловой скорости  в зависимости от времени, т. е. он должен быть равен производной от вектора угловой скорости по времени:
в зависимости от времени, т. е. он должен быть равен производной от вектора угловой скорости по времени:
 = d
= d  /dt.
/dt.
Направление вектора углового ускорения  совпадает с направлением вектора
совпадает с направлением вектора  при ускоренном вращении и противоположно ему при замедленном. Согласно рис. 2.21 тело совершает следующие вращения:
при ускоренном вращении и противоположно ему при замедленном. Согласно рис. 2.21 тело совершает следующие вращения:
– ускоренное вращение, угол φ увеличивается (рис. 2.21, а);
– ускоренное вращение, угол φ уменьшается (рис. 2.21, б);
– замедленное вращение, угол φ растет (рис. 2.21, в);
– замедленное вращение, угол φ уменьшается (рис. 2.21, г).
При вращательном движении (см. рис. 2.20) все точки тела описывают окружности с центрами на оси вращения. Как известно, скорости точек направлены по касательной к траектории движения. При вращательном движении скорость точки равна произведению модуля ω угловой скорости  тела на кратчайшее расстояние от точки до оси вращения.
тела на кратчайшее расстояние от точки до оси вращения.
VA = ω·AO; VA ┴ AO; VB = ω·BO; VB ┴ BO.
Из теории кинематики точки известно, что её ускорение направлено в сторону вогнутости траектории. Ускорения точек А, В и т. д. при вращательном движении тела раскладывают на составляющие по касательной и главной нормали к траектории движения;
 ;
;
 ,
,
где  ,
, 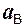 – соответственно векторы ускорений точек А и В тела;
– соответственно векторы ускорений точек А и В тела; 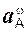 ,
,  – соответственно векторы центростремительных ускорений точек А и В;
– соответственно векторы центростремительных ускорений точек А и В;  ,
,  – векторы вращательных ускорений точек А и В.
– векторы вращательных ускорений точек А и В.
Модули центростремительных, вращательных и полных ускорений точек тела находят по формулам:
 = ω2·АО;
= ω2·АО;  = ω2·ВО;
= ω2·ВО;
 = ε·АО;
= ε·АО;  = ε·ВО;
= ε·ВО;
 ;
;
 .
.
Модуль центростремительного ускорения точки тела равен произведению квадрата модуля угловой скорости на кратчайшее расстояние от точки до оси вращения.
Модуль вращательного ускорения точки тела равен произведению модуля углового ускорения на кратчайшее расстояние от точки до оси вращения.
На рис. 2.22 и 2.23 представлены варианты механизмов с клиноременной передачей вращательного движения.
Условием безаварийной работы передаточного механизма является одинаковая скорость в точке контакта звеньев этого механизма. Так как участок АВ ремня совершает поступательное движение, то скорости точек А и В равны: V A = V B. Так как точка А принадлежит телу 1, то VA = ω1·R1, где ω1 – модуль угловой скорости  тела 1. Точка В принадлежит телу 2, поэтому VB = ω2·R2, где ω2 – модуль угловой скорости
тела 1. Точка В принадлежит телу 2, поэтому VB = ω2·R2, где ω2 – модуль угловой скорости  тела 2.
тела 2.
Приравнивая модули скоростей точек А и В, получим:
VA = ω1·R1 = VB = ω2·R2; i = ω1/ω2 = R2/R1 = d2/d1 = n2/n1,
где i – передаточное отношение механизма; R1, R2, d1, d2, n1, n2 – соответственно радиусы, диаметры и частоты вращений колёс, находящихся во вращательном движении.


Существует ряд технических решений, в которых применяется серия колёс с неподвижными осями вращений (рис. 2.24).
Нетрудно заметить, что модули скоростей точек K, L, M в рассматриваемом механизме равны. Тогда VK = VL = VM или через модули ω1 – ω4 угловых скоростей тел ω1·R1 = ω2·R2 = ω3·R3 = ω4·R4. Передаточное отношение такого механизма
i1-4 = ω1/ω4 = R4/R1 = n4/n1 = d4/d1 = z4/z1,
где z1, z4 – числа зубьев соответствующих колес.
Параметры колес 2 и 3 не попали в формулу для определения передаточного отношения, поэтому их называют паразитными колёсами.
Варианты курсового задания К 2
«Определение скоростей и ускорений точек твёрдого тела при поступательном и вращательном движениях»
Для закрепления теоретического материала, изложенного в данной теме, необходимо выполнить курсовое задание К 2. По условию этого задания требуется определить скорость и ускорение точки М одного из колёс механизма в момент времени t1 (VM(t1) =?;  (t1) =?;
(t1) =?;  (t1) =?
(t1) =?  (t1) =?).
(t1) =?).
Схемы механизмов показаны на рисунках, а необходимые данные приведены в табл. 2.2.
Таблица 2.2
| Номер варианта | Расчётная схема механизма | Исходные данные для расчёта |
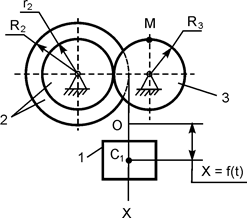
| Х = 15·t2·+ 12·t + 2, см; R2 = 60 см; r2 = 45 см; R3 = 36 см; t1 = 2 c | |

| Х = 4·t2·+ 10·t + 5, см; R2 = 80 см; R3 = 60 см; r3 = 45 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 0,5 t2 + 6·t + 8, см; R2 = 100 см; r2 = 60 см; R3 = 75 см; t1 = 2 c | |

| Х = 9,5·t2·+ 4·t + 4, см; R2 = 58 см; r2 = 45 см; R3 = 40 см; t1 = 3 c | |

| Х = 6·t2 + 15·t + 3, см; R2 = 45 см; r2 = 30 см; R3 = 80 см; t1 = 2 c |
Продолжение табл. 2.2

| Х = 9·t2 + 16·t + 7, см; R2 = 100 см; r2 = 45 см; R3 = 50 см; t1 = 2 c | |

| Х = 15·t2 + 12·t + 2, см; R2 = 45 см; r2 = 35 см; R3 = 105 см; t1 = 3 c | |

| Х = 11·t2 +10·t + 10, см; R2 = 35 см; r2 = 15 см; R3 = 10 см; t1 = 2 c |
Продолжение табл. 2.2
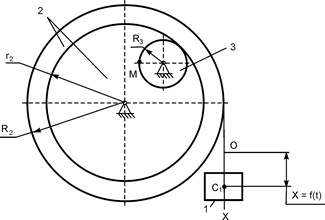
| Х = 7·t2 + 3·t + 5, см; R2 = 60 см; r2 = 45 см; R3 = 20 см; t1 = 1 c | |

| Х = 6·t2 + 7·t + 10, см; R2 = 60 см; r2 = 45 см; R3 = 16 см; t1 = 1 c | |

| Х = 10·t2 + 8·t + 9, см; R2 = 40 см; r2 = 25 см; R3 = 20 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 16·t2 + 10·t + 5, см; R2 = 20 см; r2 = 15 см; R3 = 10 см; t1 = 2 c | |

| Х = 22·t2 + 7, см; R2 = 30 см; r2 = 20 см; R3 = 40 см; t1 = 2 c | |
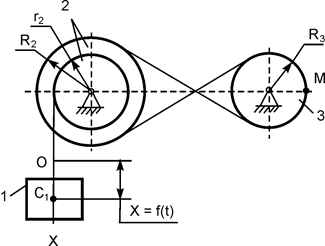
| Х = 17·t2 + 3·t + 6, см; R2 = 30 см; r2 = 20 см; R3 = 15 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 11·t2 + 2·t + 5, см; R2 = 15 см; r2 = 10 см; R3 = 15 см; t1 = 2 c | |

| Х = 12·t2 + 6·t + 4, см; R2 = 40 см; r2 = 20 см; R3 = 16 см; t1 = 3 c | |

| Х = 7·t2 + 4·t + 8, см; R2 = 15 см; r2 = 10 см; R3 = 15 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 18·t2 + 10·t + 5, см; R2 = 30 см; r2 = 20 см; R3 = 30 см; t1 = 2 c | |

| Х = 18·t2 + 10·t + 5, см; R2 = 30 см; r2 = 20 см; R3 = 30 см; t1 = 2 c | |

| Х = 27·t2 + 8·t + 10, см; R2 = 40 см; r2 = 20 см; R3 = 45м; t1 = 1 c |
Продолжение табл. 2.2

| Х = 13·t2 + 5·t + 6, см; R2 = 60 см; r2 = 45 см; R3 = 70 см; r3 = 40 см; t1 = 2 c | |

| Х = 21·t2 + 6·t + 7, см; R2 = 40 см; r2 = 20 см; R3 = 36 см; t1 = 1 c | |

| Х = 18·t2 + 9·t + 5, см; R2 = 60 см; r2 = 45 см; R3 = 40 см; r3 = 25 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 4·t2 + 8·t + 9, см; R2 = 60 см; r2 = 45 см; R3 = 80 см; r3 = 50 см; t1 = 1 c | |

| Х = 11·t2 + 4·t + 8, см; R2 = 60 см; r2 = 45 см; R3 = 50 см; t1 = 1 c | |
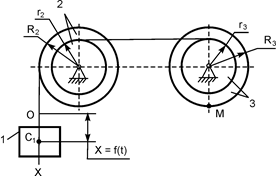
| Х = 50·t2 + 14·t + 6, см; R2 = 60 см; r2 = 45 см; R3 = 60 см; r3 = 45 см; t1 = 1 c | |

| Х = 42·t2 + 10·t + 5, см; R2 = 60 см; r2 = 45 см; R3 = 70 см; r3 = 40 см; t1 = 1 c |
Окончание табл. 2.2

| Х = 36·t2 + 5·t + 8, см; R2 = 60 см; r2 = 45 см; R3 = 70 см; r3 = 45 см; t1 = 1 c | |

| Х = 4·t2 + 6·t + 4, см; R2 = 60 см; r2 = 45 см; R3 = 55 см; r3 = 45 см; t1 = 2 c | |

| Х = 26·t2 + 7·t + 10, см; R2 = 60 см; r2 = 45 см; R3 = 55 см; t1 = 1 c |
Не нашли, что искали? Воспользуйтесь поиском: