
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вычисление криволинейного интеграла второго рода
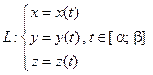
Причем, заданная ориентация на L соответствует изменению параметра t от t = α до t = β (возможно также, что α > β). Тогда
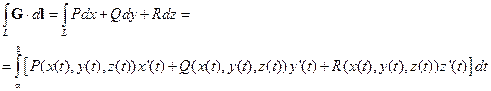
Теорема Грина (Формула Грина)
 Пусть на плоскости дана односвязная замкнутая область D, ограниченная замкнутым кусочно-гладким ориентированным контуром Γ (символически
Пусть на плоскости дана односвязная замкнутая область D, ограниченная замкнутым кусочно-гладким ориентированным контуром Γ (символически 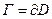 ), причем при обходе контура область остается слева (т.е. обход контура производится против часовой стрелки), Пусть, далее, компоненты P (x, y) и Q (x, y) плоского векторного поля G (x, y) = P (x, y) i + Q (x, y) j и их частные производные по у и по х, соответственно, непрерывны в области D. Тогда справедлива формула (формула Грина):
), причем при обходе контура область остается слева (т.е. обход контура производится против часовой стрелки), Пусть, далее, компоненты P (x, y) и Q (x, y) плоского векторного поля G (x, y) = P (x, y) i + Q (x, y) j и их частные производные по у и по х, соответственно, непрерывны в области D. Тогда справедлива формула (формула Грина):
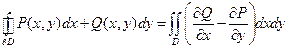
| <== предыдущая лекция | | | следующая лекция ==> |
| Домашнее задание: ОЛ-4, гл.12 § 3: 12.176, 178, 184, 193, 196, 200, 209, 207, 217, 219, 221, 222, 227, 230, 232, 238, 245. | | | Отправление в гостиницу. |
Не нашли, что искали? Воспользуйтесь поиском: