Кути між відповідними гранями (і ребрами) у всіх кристалах однієї й тієї самої речовини постійні.

Гоніометри

Із цим законом також пов'язане введення в науку вимірів кутів між гранями посередництвом прикладного гоніометра, винайденого у ХVIII ст. Каранжо. Зобра-ження цього простого приладу подане на рисунку 1.8.

Буквою К тут позначений досліджуваний кристал, затиснутий між двома металевими лінійками АВ і СD. Відліки беруться за допомогою краю АВ по транспор-тиру, приєднаному до СD.

Згодом, через порівняно малу точність виміру (не більше 0.5°), прилад Каранжо поступився своїм місцем відбивним гоніометрам.

Кращим кроком в області

гоніометричного дослід- ження кристалів став винахід у першій поло- вині минулого сторіччя однокружного відбивного гоніометра (Г.В.Вола-стон, Є.Мітчерліх).

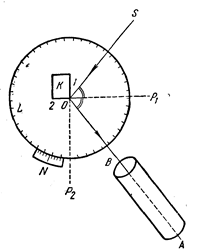
Принцип пристрою однокружного гоніометра показаний на рисунку 1.9.

Основні його частини представлені градуйованим лімбом L, ноніусом N і зоровою трубою АВ.

Вимірюваний кристал К прикріплюється в середині лімба з таким розрахунком, щоб одне з його ребер збігалося з віссю обертання лімба О. Кристал висвітлюється джерелом світла S.

Обертаючи лімб L навколо осі O, приводимо кристал у таке положення, при якому промінь SO, падаючи на одну із двох граней, що утворить ребро, сполучене з O, відбивається в напрямку ОА й потрапляє в зорову трубу АВ (вісь обертання лімба O орієнтована нормально до площини падаючих і відбитого променів SOA).

Нехай відбитий промінь отриманий від грані 1. Тоді, зловивши в трубі АВ відбиття джерела світла S від грані 1 і привівши його в центр поля зору, беремо перший відлік за ноніусом. При цьому нормаль до грані, що відбиває, 1-ОР₁ є бісектрисою кута SOA.

Таким чином, вимір усіх кутів навіть тільки одного кристала вимагає довгої й кропіткої роботи. Недарма стародавні натуралісти порівнювали роботу гоніометриста в розумінні необхідної точності, спритності й уміння з мистецтвом досвідченого фехтувальника. Незважаючи на це, як уже зазначалося, результати виміру на однокружному гоніометрі відрізняються великою точністю.

У двокружному гоніометрі кожна нормаль грані визначається сферичними координатами φ (фі) і ρ (ро), які відлічуються по горизонтальному й вертикальному колах - лімбах. Кути φ і ρ використовуються як для визначення в просторі прямої лінії, так і для визначення положення точки (проекція нормалі грані) на поверхні сфери. Таким чином, гоніометричне визначення кутів між гранями кристалів дає можливість не тільки провести їхню діагностику, але й підтвердити закон сталості двогранних кутів, побудувати об'ємну модель кристала, а також вирішити ряд інших кристалографічних завдань і математичним шляхом розрахувати символи граней, ребер та ін.

Не нашли, что искали? Воспользуйтесь поиском: