
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Цель работы: экспериментальное изучение законов динамики вращательного движения с помощью маятника Обербека.
Приборы и принадлежности: прибор Обербека, штангенциркуль, миллиметровая линейка, электрический секундомер, набор грузов. Установка Elwro.
 | 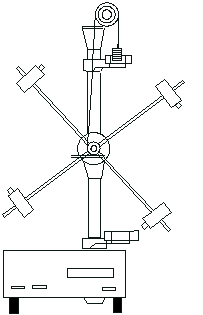 | ||
Маятник Обербека представляет крестовину, укрепленную на двойном шкиве. Ось вращения крестовины устанавливается горизонтально и закреплена в подшипниках (рис. 15). Вращение прибора осуществляется с помощью нити, намотанной на шкив. Изменение силы натяжения производится с помощью грузов различной массы, прикрепленных к свободному концу нити. Изменение момента инерции прибора достигается передвижением четырех грузов одинаковой массы и формы по направляющим крестовины. Уравнение вращательного движения прибора (при пренебрежении силами трения) связывает три величины: момент силы натяжения нити, угловое ускорение и момент инерции прибора Момент силы натяжения нити и угловое ускорение можно вычислить, зная ускорение а поступательного движения подвешенного груза.
Рис. 15
Ускорение определяется по значениям расстояния, пройденного грузом и соответствующего промежутка времени. Таким образом, можно рассчитать момент инерции прибора с помощью величин, измеренных в эксперименте. Для падающего груза
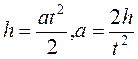
Основное уравнение динамики вращательного движения для вращающейся части маятника.

Второй закон Ньютона для поступательно движущегося груза массой М в проекции на направление движения.
М × а = М × g – T
Отсюда
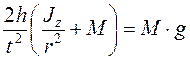
а для момента инерции Jz получается следующее выражение:

где М - масса груза, подвешенного к нити;
r— радиус шкива;
h— расстояние, пройденное грузом;
t— время, за которое груз прошел расстояние h;
g— ускорение свободного падения.
Упражнение 1
Определение момента инерции и момента силы трения в маятнике Обербека, проверка соотношения Mz=Jze.
1. Укрепить грузы на крестовине маятника. Сбалансировать маятник. Для этого сначала закрепить 2 диаметрально противоположных груза и слегка толкнуть маятник. Проследить за тем, как он будет вращаться и останавливаться. При правильной балансировке замедление вращения должно быть равномерным, а окончательное положение маятника безразличным. После этого закрепить оставшиеся два груза и снова проверить балансировку. При необходимости сместить грузы.
2. Изменяя величину груза на нити, измерить 7-8 раз угловое ускорение при фиксированном положении грузов на крестовине. Построить график зависимости e от М×r. Определить из него момент инерции и момент силы трения. Момент инерции равен Ctg угла наклона графика. Момент силы трения – точка пересечения графика с осью M r.
Снять грузы с крестовины и определить таким же образом момент инерции крестовины без груза J0
Сравнить полученный результат с формулой
J = Jo+ 4 mR2 + 4ml2 + 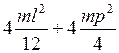
где R - расстояние от центра масс грузов на крестовине до оси вращения, l- высота груза на крестовине, p- его радиус.
Результаты занести в таблицу.
Таблица
| № п/п | m (кг) | t (c) | a (м/с2) | e (1/с2) | М r (кгмм2) | J | |
| l1= | |||||||
| Без грузов | |||||||
| l2= |
Упражнение 2
Проверить правильность соотношения 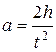 .
.
При постоянной массе груза, подвешенного на нити измерить угловое ускорение и момент инерции для двух различных положений грузов на крестовине. Проверить выполнение соотношения
 .
.
Результаты занести в таблицу.
Экспериментальную проверку уравнения движения можно осуществить двумя способами:
1. При неизменном моменте инерции прибора должно сохраняться соотношение.
J= 
2. При постоянной массе груза, подвешенного к нити (при постоянном моменте силы) должно выполняться соотношение
J11 – J12 = 4 m (R 12 – Rl22)
где m – масса грузов крестовины, R 1 и R 2 – расстояние от оси вращения до центра тяжести грузов крестовины.
Контрольные вопросы:
1. Что называется моментом силы относительно точки и относительно неподвижной оси?
2. От чего зависит момент инерции тела, какую роль он играет во вращательном движении?
3. Как в данной работе определяется ускорение поступательного движения грузов, подвешенных к нити прибора; получите выражение для расчёта - этого ускорения.
4. Чем обусловлен разница в экспериментальном и теоретически полученных значениях момента инерции?
5. На каком законе основана данная работа? Сформулируйте этот закон.
6. Какая связь существует между линейным и угловым ускорениями? При каком условии она существует?
7. Момент какой силы приводит маятник Обербека во вращательное движение? Как можно изменить момент силы в данной работе?
9. Какая теорема используется для вычисления момента инерции цилиндров? Как влияет на момент инерции цилиндров расстояние, на котором они расположены на стержнях?
10. Как влияет на угловое ускорение увеличение момента силы при неизменном моменте инерции? Как влияет на угловое ускорение увеличение момента инерции при неизменном моменте силы?
Не нашли, что искали? Воспользуйтесь поиском: